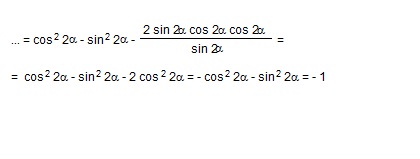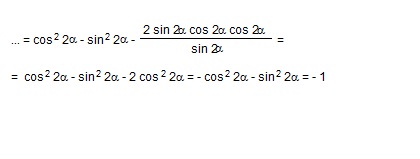как доказать тождество - страница 11

Доказать тождество

\( \frac{sin \alpha}{1+cos \alpha}+\frac{1+cos \alpha}{sin \alpha}=\frac{2}{sin \alpha} \)

= (sin^2a  +1+2cosa+cos^2a) : (sina*(1+cosa))  =  (2+2cosa) : (sina*(1+cosa))  =

 =  2(1+cosa) : (sina*(1+cosa))  =  2/sina

2/sina   =   2/sina

Решение Вашего задания во вложении

Ctgx - sinx/1-cosx = - 1/ sinx
Доказать тождество

$$ Ctgx- \frac{sinx}{1-cosx}=- \frac{1}{sinx} $$
упростим левую часть тождества,
по определению  ctgx=$$ \frac{cosx}{sinx} $$,  приведем к общему знаменателю,  применим основное тригонометрическое тождество
$$ \frac{cosx}{sinx}- \frac{sinx}{1-cosx} = \frac{cosx- cos^{2}x- sin^{2}x }{sinx(1-cosx)} = \frac{cosx-1}{sinx(1-cosx)} =- \frac{1}{sinx} $$
после преобразований получили выражение,  равное выражению в правой части равенства,  тождество доказано

доказать тождество:

1) 3cos 2α – sin^2 α + cos^2 α = 2cos 2α

2) (Sin 5α – sin 3α) / 2cos 4α = sinα

упростить:

Cos^2 (π-α) – cos^2 ( П/2 - α)

3cos 2α – 2cos 2α - sin^2 α + cos^2 α = 0

3cos 2α – 2cos 2α -(1-cosα)/2+(1+cosα)/2=0

6cos 2α – 4cos 2α -1+cosα+1+cosα=0

6cos 2α – 4cos 2α + 2cosα=0

2cos 2α =0

cos 2α =0

2α= П/2+ Пn, n Z

α= П/4+ Пn/2, n Z

2.(Sin 5α – sin 3α) / 2cos 4α = sinα

 sin 5α – sin 3α = 2cos 4αsinα

sin 5α – sin 3α =- sin 3α+sin 5α

0=0

Cos^2 (π-α) – cos^2 ( П/2 - α)=Cos^2α – sin^2 α=cos2 α

доказать тождество ((cos^2*t)/(1-sin*t))-sin^2*t-cos^2*t=sin*t.

1-sint в числителе и знаменателе сократятся останется: 1+sint-sin^2*t-cos^2*t=sint

 воспользуемся основным тригонометрическим тождеством:cos^2t=1-sin^2t

получается 1+sint-sin^2t-(1-sin^2t)=sint

1 и sin^t сокращаются, остаётся sint=sint, что и требовалось доказать

Доказать тождество cos4a-sin4a*ctg2a=-1