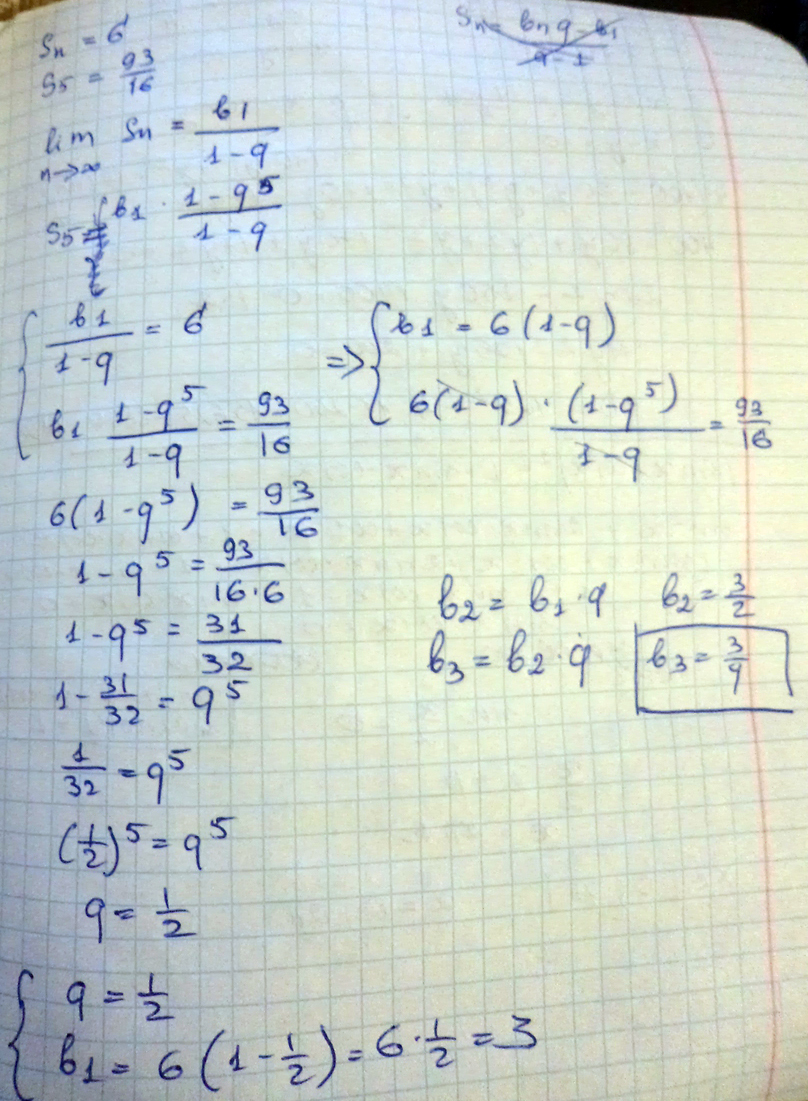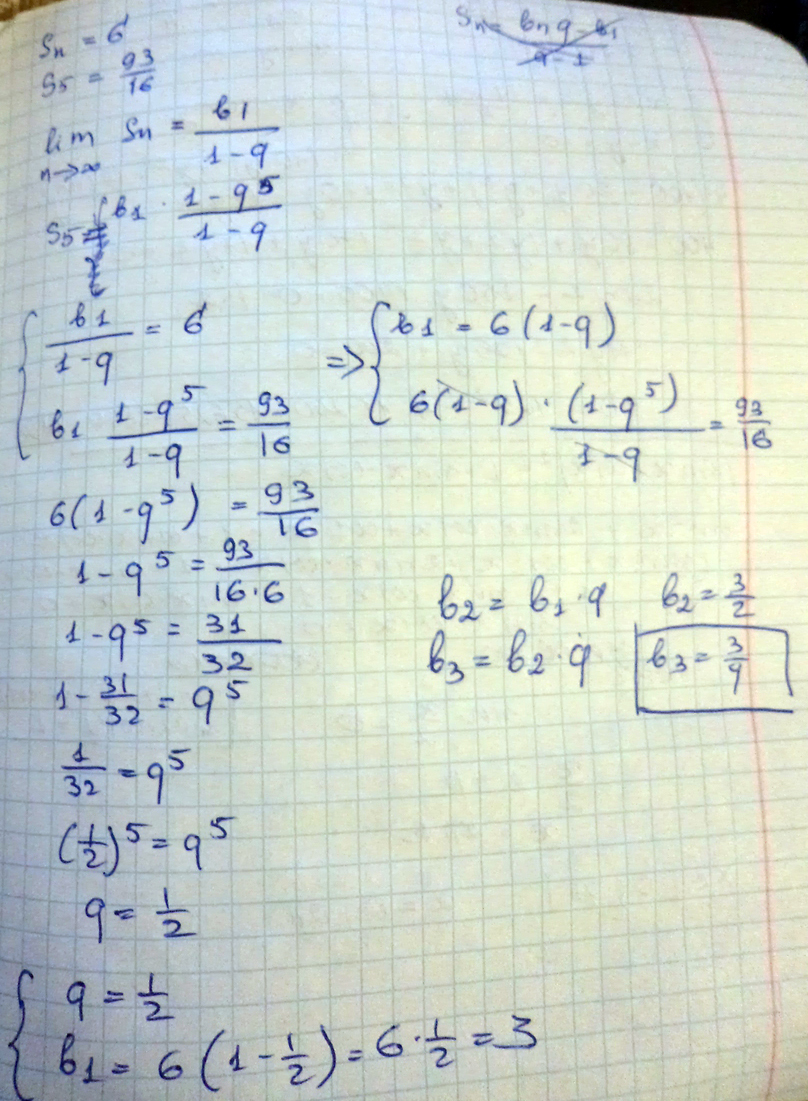прогрессия »
бесконечная прогрессия - страница 14
Cумма бесконечно убывающей геометрической прогрессий равна 32, а сумма ее первых пяти членов - 31. Найдите первый член прогрессии.
Решение: S = b1/(1-q) - формула суммы бесконечно убивающей геометрической прогрессии, где b1 - ее первый член, а q - знаменатель прогрессии.
S = b1*(q^5-1)/(q-1) - формула суммы первых пяти членов геометрической прогрессии.
b1/(1-q) = 32 => 1-q = b1/32 => q=1-(b1/32)
b1*((1-(b1/32))^5-1)/(1-(b1/32)-1) = 31
b1*((1-(b1/32))^5-1)/(-b1/32)=31
-32((1-(b1/32))^5-1)=31
(1-(b1/32))^5-1=-31/32
(1-(b1/32))^5=1/32
1-b1/32=1/2
b1/32=1/2
b1=16Сумма бесконечно убывающей геометрической прогрессии равна 32, а сумма её первых пяти членов 31. Найдите первый член прогрессии.
Решение: S = b1/(1-q) - формула суммы бесконечно убивающей геометрической прогрессии, где b1 - ее первый член, а q - знаменатель прогрессии.
S = b1*(q^5-1)/(q-1) - формула суммы первых пяти членов геометрической прогрессии.
b1/(1-q) = 32 => 1-q = b1/32 => q=1-(b1/32)
b1*((1-(b1/32))^5-1)/(1-(b1/32)-1) = 31
b1*((1-(b1/32))^5-1)/(-b1/32)=31
-32((1-(b1/32))^5-1)=31
(1-(b1/32))^5-1=-31/32
(1-(b1/32))^5=1/32
1-b1/32=1/2
b1/32=1/2
b1=16Сумма бесконечно убывающей геометрической прогрессии равна 32, а сумма ее первых пяти членов -31. Найдите первый член прогрессии
Решение: S = b1/(1-q) - формула суммы бесконечно убивающей геометрической прогрессии, где b1 - ее первый член, а q - знаменатель прогрессии.
S = b1*(q^5-1)/(q-1) - формула суммы первых пяти членов геометрической прогрессии.
b1/(1-q) = 32 => 1-q = b1/32 => q=1-(b1/32)
b1*((1-(b1/32))^5-1)/(1-(b1/32)-1) = 31
b1*((1-(b1/32))^5-1)/(-b1/32)=31
-32((1-(b1/32))^5-1)=31
(1-(b1/32))^5-1=-31/32
(1-(b1/32))^5=1/32
1-b1/32=1/2
b1/32=1/2
b1=16
$$ 1) S= \frac{b_1}{1-q} $$
$$ 32= \frac{b_1}{1-q}\Rightarrow 32\cdot(1-q)=b_1 $$
$$ 2) S_n= \frac{b_1(1-q^n)}{1-q} \\ \\ S_5= \frac{b_1(1-q^5)}{1-q} \\ \\31= \frac{b_1(1-q^5)}{1-q} $$
Подставим во второе уравнение вместо
b₁=32·(1-q)
получим
$$ 31= \frac{32(1-q)\cdot (1-q^5)}{1-q} \\ \\ 31=32\cdot(1-q^5) \\ \\ 1-q^5= \frac{31}{32} \\ \\-q^5= \frac{31}{32}-1 \\ \\ q^5= \frac{1}{32} \\ \\ q= \frac{1}{2} $$
b₁=32·(1-(1/2))=16
Ответ. b₁=16; q=1/2
Сумма бесконечной геометрической прогрессии (bn) равна 7, а сумма квадратов всех ее членов равна
14. Найдите b1 и b2
Решение: Квадраты членов убывающей геомметричесской прогрессии также являются членами убывающей геометрической прогрессии
$$ S=\frac{b_1}{1-q} $$ [$$ |q|<1; $$
из условия следует что
$$ \frac{b_1}{1-q}=7 $$
$$ \frac{b^2_1}{1-q^2}=14 $$
$$ \frac{b_1}{1-q}*\frac{b_1}{1+q}=14 $$
$$ \frac{b_1}{1+q}=2 $$
$$ b_1=7(1-q)=2(1+q) $$
$$ 7-7q=2+2q $$
$$ 2q+7q=7-2 $$
$$ 9q=5 $$
$$ q=\frac{5}{9} $$
$$ b_1=7*(1-\frac{5}{9})=7*\frac{4}{9}=\frac{28}{9} $$
$$ b_2=b_1*q=\frac{28}{9}*\frac{5}{9}=\frac{140}{81} $$
20б. Найдите третий член бесконечной геометрической прогрессии сумма которой равна 6, а сумма первых пяти членов равна 93/16
Решение: Можно найти только сумму бесконечно спадающей бесконечной геометрической прогрессии по формуле S=$$ \frac{ b_{1} }{1-q} $$
$$ \frac{ b_{1} }{1-q} =6 $$
$$ \frac{ b_{1} }{q-1} =-6 $$
Сумма первых пяти членов геометрической прогрессии вычисляется по формуле
$$ S_{5}= \frac{ b _{1}(q^{6}-1)}{q-1}= \frac{93}{16}$$
$$ S_{5}={-6(q^{6}-1)}= \frac{93}{16} $$
$$ {q^{5}-1}= -\frac{31}{32} $$
$$ {q^{5}}= 1-\frac{31}{32} $$
$$ {q^{5}}=\frac{1}{32} $$
$$ {q^{5}}=\frac{1}{32} $$
$$ {q}=\frac{1}{2} $$
$$ \frac{ b_{1} }{1-0,5} =6 $$
$$ \frac{ b_{1} }{0,5} =6 $$
$$ { b_{1} } =3 $$
$$ { b_{3} } =3*0,5*0,5=0,75 $$
Ответ: $$ { b_{3} } =0,75 $$