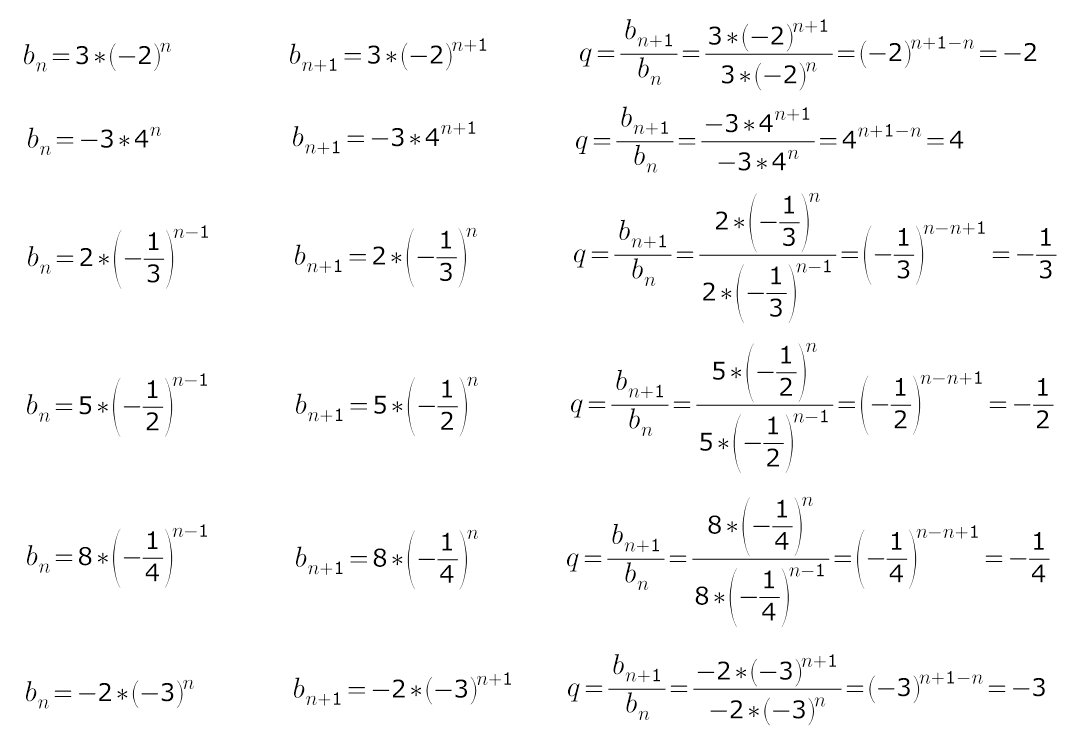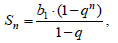прогрессия »
бесконечная прогрессия - страница 16
Является ли последовательной бесконечно убывающей геометрической прогрессии, если она задана формулой n-го числа bn=3*(-2)^n ; bn=-3*4^n; bn=2*(-1/3)^n-1; bn=5*(-1/2)^n-1 ;
bn=8(-1/4)^n-1; bn=-2*(-3)^n
Решение: Последовательность называют бесконечно убывающей геометрической прогрессией, если -1 < q < 1.
нужно в каждом случае найти q.
Ответ "ДА" в третьем, четвертом и пятом случаях)))
когда q = -1/3, q = -1/2, q = -1/4
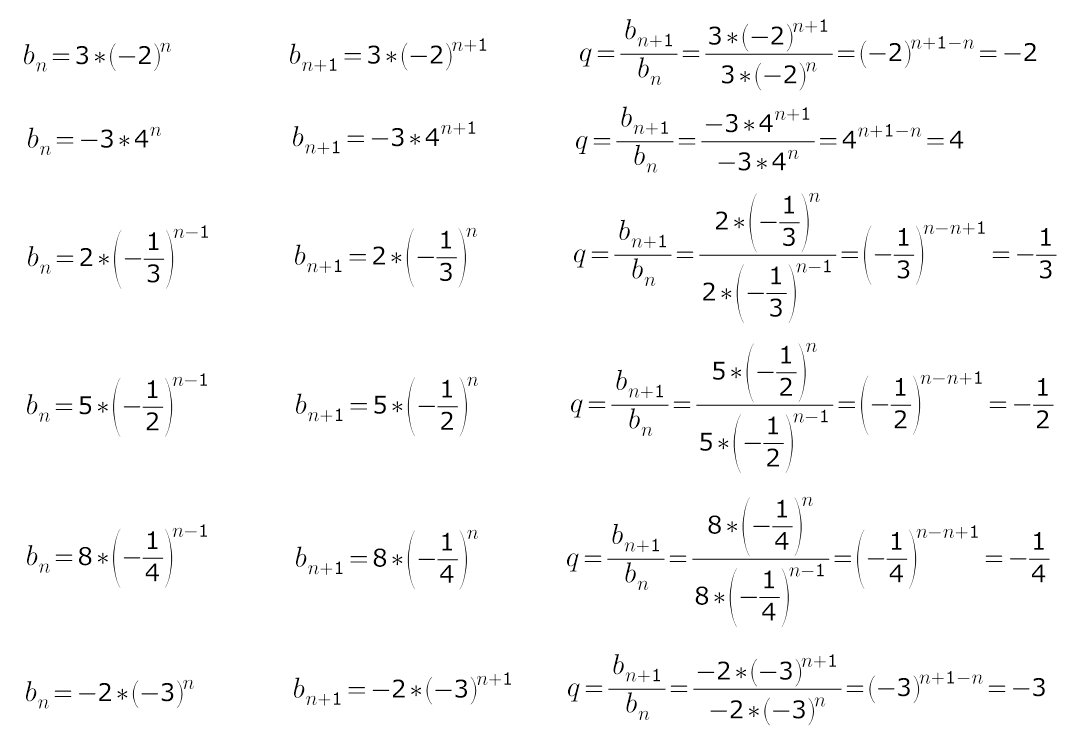
1. Дана геометрическая прогрессия 2;4;8;. а) Найдите 6 член прогрессии б) найдите сумму первых 6 членов прогрессии. 2. Найдите сумму бесконечной геометрической прогрессии (bn), если b1=24 q=1/2 3. В геомктрической прогрессии(сn) с5=162 q=-3 а) Найдите с1 б) Какие из членов данной прогрессии отрицательны?
Решение: 11111111111111Дано:
2;4;8. г. пр.
b1=2
b2=4
b3=8
Найти:
1)S6-
2)b6
Решение:
Сначала найдем знаменатель г. пр.
Формула - q=b2/b1
q=4/2
q=2
1) Теперь найдем S6 (1 формула во вложении)
S6= 2*(1-2^6) / 1-2
=2*(1-64) / -1
=2* (-63) / -1
=-126 / -1 = 126
2) Найдем 6 член г. пр. (2 формула во вложении)
b6=2*2^5
=2*32=64
Ответ: 1)S6=126; 2)b6=64.
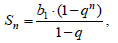
1. Дана геометрическая прогрессия 2;4;8;. а) Найдите 6 член прогрессии б) Сумму первой 6-ти членов членов прогрессий 2. Найдите сумму бесконечной геометрической прогрессии (bn), если b1=24 q=1/2 3. В геометрической прогрессий (Сn) c4=24 ; q=-2 а) Найдите С1 б) Какие из чисел данной прогрессии отрицательны? 4. Дана бесконечная геометрическая прогрессия (Сn) с суммой S=15 и первым членом С1=18. Найдите q.
Решение: 1. g=b(n+1)\bn=4\2=2 a)b6=b1*g^n-1=2*2^5=64 б) S6=(b6*g-b1)\g-1=(64*2-2)\2-1=1262. S(бесконечной)=b1*(g^n-1)\g-1 = (24*(1/2^n - 1 ))\ 1/2
3/ a) c1=c4\g^3=24\(-2)^3=-3 б) все нечётные члены прогрессии будут отрицательны т. е c1.c3.c5.c7.c9 и т. д
4.Sn=c1(g^n-1)\g-1 подставляем известные значения, упрощаем, выражаем g. 15=18*(g^n-1)\g-1= 18g^n-15g-3=0 (квадратное ур-ние. решаем) D=441 g1=-1\6 g2= 1 Ответ: 1,1\6.
Сумма кубов всех членов бесконечной геометрической прогрессии относится к сумме квадратов ее членов как 12/13. Найдите третий член прогрессии, если сумма первых двух ее членов 4/3.
Решение: S=a(1)/(1-q)=3-сумма членов искомой прогрессии.
a(1)=3*(1-q)
Кубы ее членов - новая убывающая геом. прогрессия.
Тогда S’=a’(1)/(1-q’)=108/3
При этом a’(1)=a(1)^3 и q’=q^3.
{a(1)+a(1)*q+a(1)*q^2+.+a(1)*q^(n-1)
a(1)^3+a(1)^3*q^3+a(1)^3*q^6+.}
S’=(27*(1-q)^3)/(1-q^3)=
=(27*(1-q)^2)/(1+q+q^2)=108/13
243q^2-810*q+243=0
q(1)=1/3<1
q(2)=3>1-отбрасываем.
Тогда а (1)=3*(1-1/3)=2
Прогрессия a(1)=2;q=1/3Выяснить, является ли геометрическая прогрессия бесконечно убывающей, (2 примера) если
1) b7=-30,b6=15
2)b5=-9,b9=-1/27
всё по дейсвтиям)
Решение: 1) $$ b_7=b_1*q^6\ \ \ \ b_6=b_1*q^5 \\\ b_1*q^6=-30\ \ \ \ b_1*q^5=15\\\ \frac{b_1*q^6}{b_1*q^5}=\frac{-30}{15}\\\ q=-2\\\ |q|>1 $$
Следовательно геометрическая прогрессия бесконечно убывающей не является.
2) $$ b_5=b_1*q^4\ \ \ \ b_9=b_1*q^8 \\\ b_1*q^4=-9\ \ \ \ b_1*q^8=-\frac{1}{27}\\\ \frac{b_1*q^8}{b_1*q^4}=-\frac{1}{27}:(-9)\\\ q^4=\frac{1}{243}\\\ q=\frac{1}{ \sqrt[4]{243}}\\\ |q|<1 $$
Следовательно геометрическая прогрессия бесконечно убывающей является