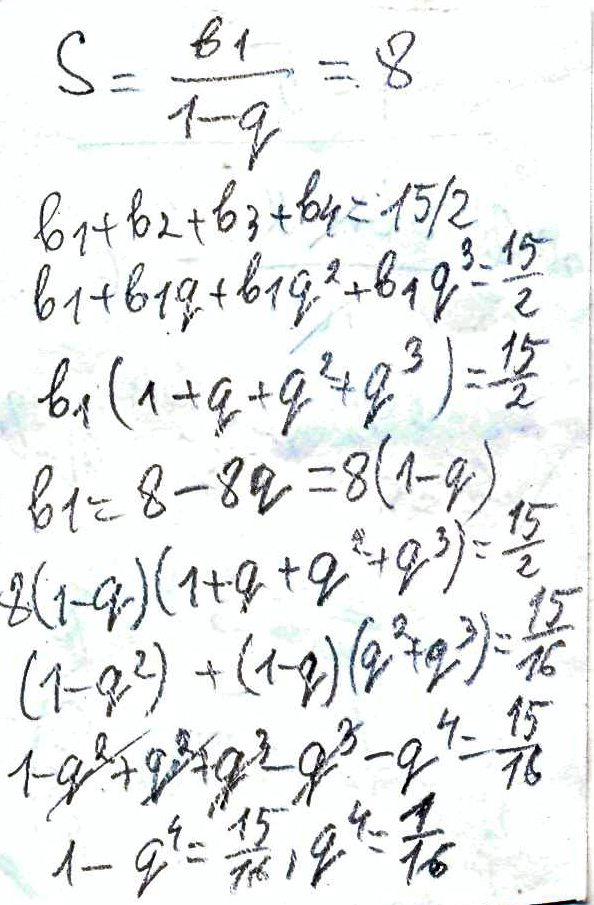прогрессия »
бесконечная прогрессия - страница 15
Найдите сумму S бесконечно убывающей геометрической прогрессии, если сумма первого и второго членов равна 3, а произведение первого и третьего членов равно 36.
Решение: $$ b_{1}, b_{2}= b_{1}q, b_{3}= b_{1} q^{2} $$
$$ \left \{ { b_{1}+ b_{1}q =3 \atop b_{1}* b_{1}q=36} \right. \left \{{ b_{1}= \frac{3}{1+q}} \atop { b^{2} q^{2}=36} \right. $$
подставляем первое уравнение во второе
$$ \frac{9}{ (1+q)^{2}}* q^{2}=36 ; \frac{q^{2}}{ (1+q)^{2}}=4 ;\\ \frac{q}{1+q}=+-2 ; q=2+2q; q_{1}=-2; b_{1}=\\= \frac{3}{1-2} ; b_{1.1}=-3 q=-2-2q; q_{2}=\\=- \frac{2}{3} b_{1}= \frac{3}{1- \frac{2}{3}} ; b_{1.2}=9 -3;6;-18 - не подходит 9;\\ -6;4 - подходит S= b_{1}/(1-q)= \frac{9}{1-(- \frac{2}{3}) } =\\=9/ \frac{5}{3}= \frac{27}{5}=5 \frac{2}{5} $$Найти три первых члена бесконечной геометрической прогрессии, сумма которой равна 9, а сума четырех первых членов равна 80/9
Решение: Сумма бесконечной геометрической прогрессии вычисляется по формуле
S∞=b₁/(1-q) 9=b₁/(1-q)
Сумма четырех первых членов вычисляется по формуле
S₄=b₁(1-q³)/(1-q) 80/9=b₁(1-q³)/(1-q)
Имеем два уравнения с двумя неизветными. Из первого находим b₁ и подставим во второе
b₁=9(1-q)
80/9=9(1-q)(1-q³)/(1-q)
80/9=9(1-q³)
1-q³=80/81
q³=1-80/81=1/81
q=1/9
Тогда b₁=9(1-1/9)=8
Находим искомую сумму трех первых членов
S₃=b₁(1-q²)/(1-q)=8(1-1/81)/(1-1/9)=9(1-1/81)=9-1/9=8целых8/9
определить сумму бесконечно убывающей геометрической прогрессии, если известно, что сумма ее первого и четвертого членов равна 54, а сумма второго и третьего равна 36.
Решение: b1+b4 = b1+b1*q^3 = b1(1+q^3) = b1(1+q)(1-q+q^2) = 54b2+b3 = b1*q + b1*q^2=b1q(1+q) = 36
разделим первое на 2е
(1-q+q^2)/q = 54/36
q^2 - q + 1 = 1,5q
q^2 - 2,5q + 1 = 0
По теореме Виета
q1=2
q2=0,5
Для бесконечно убывающей прогрессии |q|<1
b1 = 36/q(1+q) = 36/0,5*1,5 = 48
S = b1/(1-q)= 48/0,5 = 96
все члены бесконечно убывающей геометрической прогресси положительны, а сумма равна 8, сумма её первых четырех членов равна 15/2. найдите первый член прогрессии.
Решение: Т. к. прогрессия бесконечно убывающая геометрическая и с положительными членами, то q=1/2. Найдем q из S=b1/(1-q)=8, откуда b1=8*( (1-q)=8*(1-1/2)=8*1/2=4Ответ: 4.
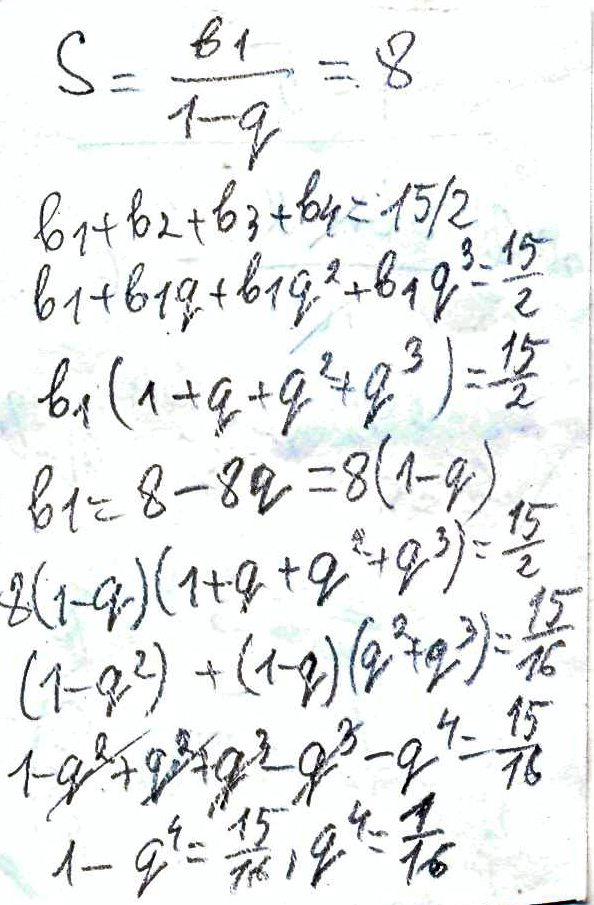
Найдите знаменатель бесконечно убывающей геометрической прогресси, если сумма всех членов прогресси равна 2, а сумма квадратов всех членов этой прогресси равна 5.
Решение: Для исходной бесконечно убывающей геометрической прогрессии \(b_n \) имеем по условию: \( S=b_1+b_2+b_3+.=\dfrac{b_1}{1-q}=2 \), где q - знаменатель исходной прогрессии.
Теперь рассмотрим прогрессию \(c_n\), составленную из квадратов членов исходной прогрессии, т. е. \( c_1=(b_1)^2,\ c_2=(b_2)^2,\ c_3=(b_3)^2,\). Эта новая прогрессия - также геометрическая бесконечно убывающая. Следовательно,\( \tilde{S}=c_1+c_2+c_3+.=\dfrac{c_1}{1-\tilde{q}}=5 \), где \(\tilde{q}\) - знаменатель уже новой прогрессии.
\( \tilde{q}=\frac{(b_2)^2}{(b_1)^2}=(\frac{b_2}{b_1})^2=q^2 \)
Преобразуем:
\( \tilde{S}=5=\dfrac{c_1}{1-\tilde{q}}=\dfrac{(b_1)^2}{1-q^2} \)
Получим систему уравнений: \(\begin{cases} \frac{b_1}{1-q}=2 \\ \frac{(b_1)^2}{1-q^2}=5 \end{cases}\)
Делим первое на второе и запишем в первой строке системы:
\( \begin{cases} \frac{b_1(1-q)(1+q)}{(1-q)(b_1)^2}= \frac{2}{5} \\ b_1=2-2q \end{cases}\) <=>\( \begin{cases} \frac{1+q}{b_1}= \frac{2}{5} \\ b_1=2-2q \end{cases} \\ \frac{1+q}{2-2q}= \frac{2}{5} \\ 5+5q=4-4q \\ 9q=- 1 \\ q=- \frac{1}{9}\)
Ответ: $$ - \frac{1}{9} $$