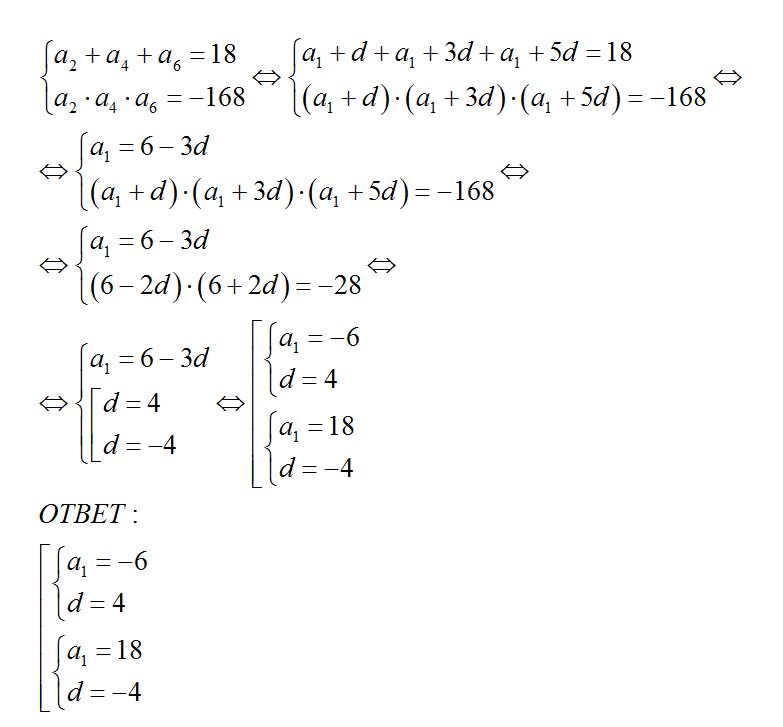найти первый член и разность прогрессии - страница 10
Сумма 8 и 6 члена арифметической прогрессии=16 а произведение 2 и 12=-36. Найти разность и первый член прогрессий.
Решение: А8+а6=16
а2*а12=-36
найти d и a1,
a8=a1+7d
a6=a1+5d
а2=а1+d
a12=a1+11d
a1+7d+a1+5d=16 2a1+12d=16 разделим на 2
получим a1+6d=8
a1=8-6d
(a1+d)*(a1+11d)=-36
a1^2+12a1d+11d^2=-36
(8-6d)^2+12(8-6d)*d+11d^2=-36
64-96d+36d^2+96d-72d^2+11d^2=-36
-25d^2=-100
d^2=4
d=2 разность арифметической прогрессии
a1=8-6*2=-4 первый член арифметической прогрессии
Ответ: 2,4.
Сумма второго, четвертого и шестого членов арифметической прогрессии равно 18, а их произведение равно -168. Найдите первый член и разность прогрессии.
Решение: Решим как систему уравнений!Получим два варианта ответа)
===============================
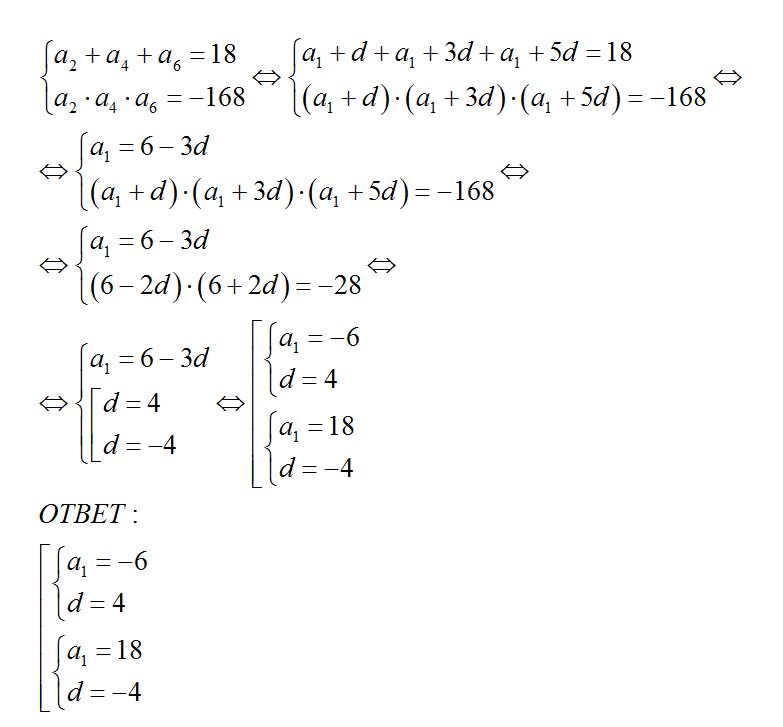
В арифметической прогрессии имеется 20 членов. Сумма членов с четными номерами 250, а сумма членов с нечетными номерами 220. Найдите первый член и разность этой прогрессии.
Решение: а что женская логика в этот раз не помогла?)как четные, так и нечетные члены это прогрессии, сами образуют прогрессии, то есть:
a2, a4, a20, это арифметическа прогрессия, с d’=2d,a1’=a2
Sчетн=(2a2+2d*9)*10/2=250
a2+9d=25, a2=a1+d, a1+10d=25
аналогично a1,a3,a19, d’’=2d, a1=a1
Sнеч=(2a1+2d*9)*10/2=220
a1+9d=22
системка:
a1+10d=25
a1+9d=22
откуда d=3, a1=-5Найти разность арифметической прогрессии с первым членом, равным 1, у которого Sm:Sn= m^2:n^2, где Sm-сумма m первых членов, Sn-сумма n членов
Решение: По известной формуле распишем сумму m и n первых членов арифметической прогрессии:$$ S_{m}=\frac{2a_{1}+d(m-1)}{2}*m, $$
$$ S_{n}=\frac{2a_{1}+d(n-1)}{2}*n. $$
Из условия получим следующее уравнение:
$$ \frac{(2a_{1}+d(m-1))*m}{(2a_{1}+d(n-1))*n}\ =\ \frac{m^2}{n^2}. $$
Или, раскрыв пропорцию, получим:
$$ 2a_{1}n+dn(m-1)\ =\ 2a_{1}m+dm(n-1). $$
$$ 2a_{1}(n-m)\ +\ d(mn-n-mn+m)\ =\ 0, $$
$$ (n-m)(2a_{1}-d)\ =\ 0. $$
Так как $$ neq\ m, $$ получим:
$$ d\ =\ 2a_{1}\ =\ 2. $$
Ответ: 2.
Пусть D - разность прогрессии.
Тогда Sm = (1+1+D*(m-1))*m=(D*m-D+2)*m
Следовательно
(D*m-D+2)*m m^2 D*m-D+2 m
- = - откуда - = -
(D*n-D+2)*n n^2 D*n-D+2 n
D*m*n-D*n+2*n=D*m*n-D*m+2*m
D*(m-n)=2*(m-n). Поскольку m и n - разные числа, то D = 2
Между первым и вторым членами арифметической прогрессии разность которой равна 42 поместили пять чисел так что эти семь чисел стали последовательностью новой арифметической прогрессии найти разность новой арифметической прогрессии
Решение: как известно для арифметической прогрессии$$ a_{n}=a_{1}+d*(n-1) $$
следовательно для первой прогрессии будет
$$ a_{2}=a_{1}+42*1 $$
для второй прогрессии
$$ b_{7}=b_{1}+d*6 $$
при этом мы знаем из условия, что а2=b7 и a1=b1, следовательно сделав звмену получим
$$ a_{1}+42=a_{1}+d*6 $$
6d = 42
d = 7
Ответ разность второй прогрессии 7