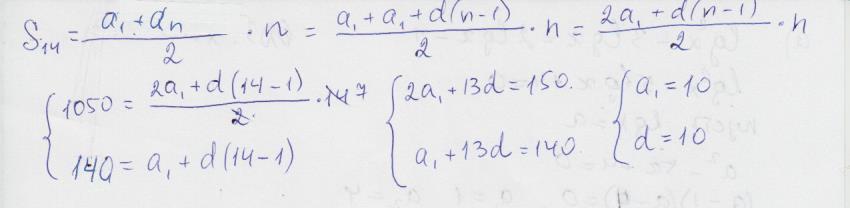найти первый член и разность прогрессии - страница 4
В арифметической прогрессии 14-ый член равен 140, а сумма первых 14-ти членов равна 1050. Найдите первый член и разность этой прогрессии.
Решение: A14=140
S14=1050
a1+13d=140
s(14)=(2a1+13d)*14/2=1050
(a1+140)*7=1050
a1+140=1050:7=150
a1=150-140=10
10+13d=140
13d=140-10=130
d=130:13=10
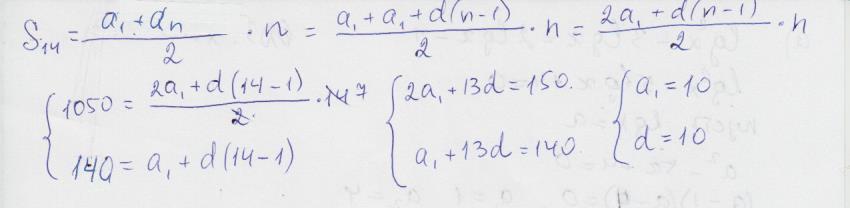
1) Найдите 23-й член арифметической прогрессии -4,4; -4,2;.
2) 20-ый член арифметической прогрессии {а энное} равен 2,9 ( а20 = 2,9), а 17-ый член равен 2,3 (а17 = 2,3). Найдите первый член и разность этой арифметической прогрессии.
3) найдите сумму первых двадцати восьми членов арифметической прогрессии -2,3; -2,5;.
4) Сколько первых членов арифметической прогрессии -13; -11; -9;. нужно сложить, чтобы получить -40?
Решение: 1) а1=-4,4; а2=-4,2;
а23- d=a2 - a1= -4,2-(-4,4)=0,2 => a23=a1+22d= -4,4+22×0,2=0
2) d-разность ар. прогрессии; d
a20=a17+3d => 3d=a20-a17=2,9-2,3=0,6;
a17=a1+16d => a1=a17-16d=2,3-16×0,6=-7,3
3) S28-; d=a2-a1=-2,5+2,3=-0,2;
S28=28(a1+27d)/2=14(-2,3-27×0,2)=14×(-7,7)=-107,8
4) Sn=-40; n-; d=a2-a1=-11+13=2;
Sn=n(a1+d(n-1))/2=n(-13+2n-2)/2=n(2n-15)/2=(2n^2-15n)/2 =>
-40×2=2n^2-15n
2n^2-15n+80=01) d=-4,2+4,4=0,2
a₂₃=a₁+d(23-1)=-4,4+0,2*22=-4,4+4,4=0
2)
a₁+19d=2,9
a₁+16d=2,3 из первого отнять второе
3d=0,6
d=0,2
a₁=2,3-16*0,2=-0,9
3) d=-2,5+2,3=-0,2
S₂₈=(2a₁+27*d):2*28 28:2=14
S₂₈=[2*(-2,3)+27*(-0,2)]*14=-10*14=-140
4) S=-40 d=-11+13=2
-40=[2a₁+2(n-1)]*n:2
(2*(-13)+2n-2)*n=-80
-28n+2n²=-80
n²-14n+40=0
D=14²-4*40=196-160=36
√D=6
n₁=(14-6):2=4
n₂=(14+6):2=10
два ответа 10 или 4
1)найти наименьшее значение неравенства:
(x+1)^2 * (x-2)≥0
2)
Упростить и найти значение выражения
\( \frac{x-7 \sqrt{x} +6}{ \sqrt{x} -1} \)
ЕСЛИ:\( x=(12 \frac{4}{5} +1 \frac{5}{12} - 0,8-3 \frac{1}{3} ) \)
3)
НАЙТИ КОЛИЧЕСТВО ЧЛЕНОВ АРИФМЕТИЧЕСКОЙ ПРОГРЕССИИ ЕСЛИ ПЕРВЫЙ ЕЕ ЧЛЕН РАВЕН 33, РАЗНОСТЬ РАВНА -7, А СУММА 45.
Решение: 1. (x+1)^2 * (x-2)≥0; учитывая. что первый множитель неотрицателен имеем, что данное неравенство равносильно совокупности: х-2>=0 или x=-1; х>=2 или x=-1.
Решение будет {-1}U[2;~).
2. (x-7*K(x)+6)/(K(x)-1)=((K(x))^2-7K(x)+6)/(K(x)-1)=(в числителе получили квадратный трёхчлен относительно K(x), корнями которого будут числа 6 и 1)=
=((K(x)-6)*(K(x)-1))/(K(x)-1)=K(x)-6. Если х=12,8+1(5/12)-0,8-3(1/3)=12-1(11/12)=
=10(1/12), то K(x)-6=K(121/12)-6=11/(2К(3))-6=(11-12К(3))/(2К(3)).
Найти шестой член и разность арифметической прогрессии, если сумма ее пятого и седьмого членов равно 18, а второй член равен -3.
Решение: Разность между шестым и третьим членами прогрессии равна утроенной разности прогрессии; отсюда разность прогрессии равна
d = (a₆−a₅)/3 = (−1,2 − 3)/3 = −1,4.
Пятый член прогрессии равен разности между шестым членом и разностью прогрессии:
a₅ = a₆ − d = −1,2 − (−1,4) = 0,2.
ОТВЕТ: 0,2.
1) Найдите первый член и разность арифметической прогрессии (аn), если а9+а7=70, а5-а2=15
7) Найдите область определения функции у= под корнем -х2+5х+24
Решение: 1) нужно составить систему:а₉+а₇=70
а₅-а₂=15
затем выразить а через разность:
а₁+8d+a₁+6d=70
a₁+4d-a₁+d=15
получается:
2a₁+14d=70
5d=15
откуда найдем d=3
подставим в первое уравнение 2а₁+14*3=70
а₁=14
7)√-х2+5х+24
т. к. это выражение под корнем, то можно записать так:
-х2+5х+24≥0(надеюсь, понятно почему)
затем вычисляем корни и получается х₁=-3, х₂=8
Дальше будем работать по методу интервалов: -х2+5х+24=-(х+3)(х-8), можем избавиться от минуса, умножив -(х+3)(х-8) на -1.
получается -(х+3)(х-8)≥0, т. к обе части умножили на отрицательное число, меняем знак и получаем (х+3)(х-8)≤0
Теперь на числовой прямой отмечаем точки х=-3 и х=8 и ставим знаки. Справа налево: +,+. Т. к. нам нужны отрицательные значения(потому что (х+3)(х-8)≤0), то ответ будет таким:
D(y)=[-3;8]