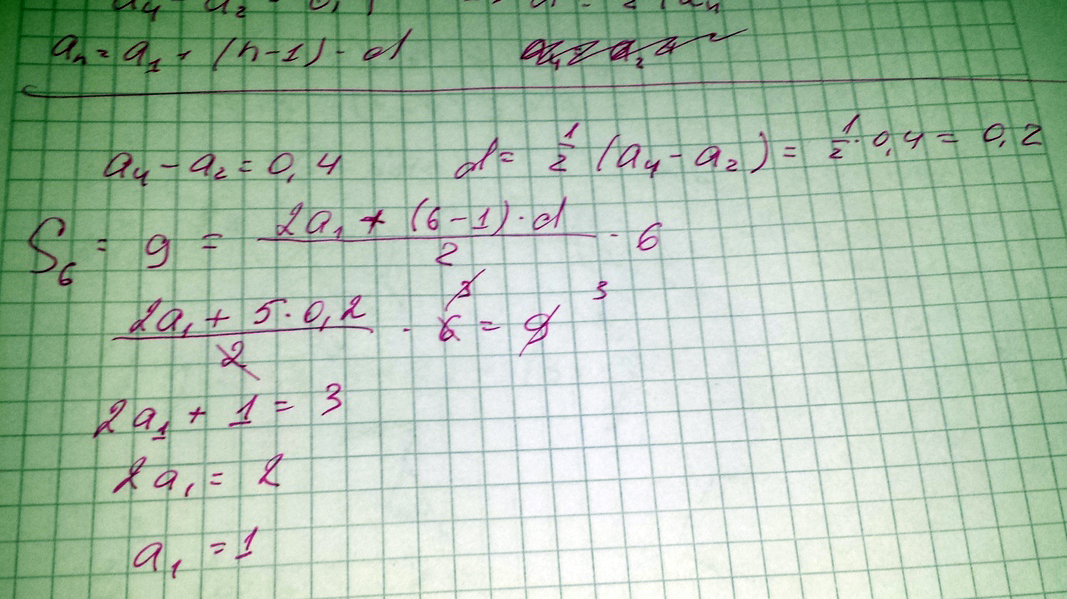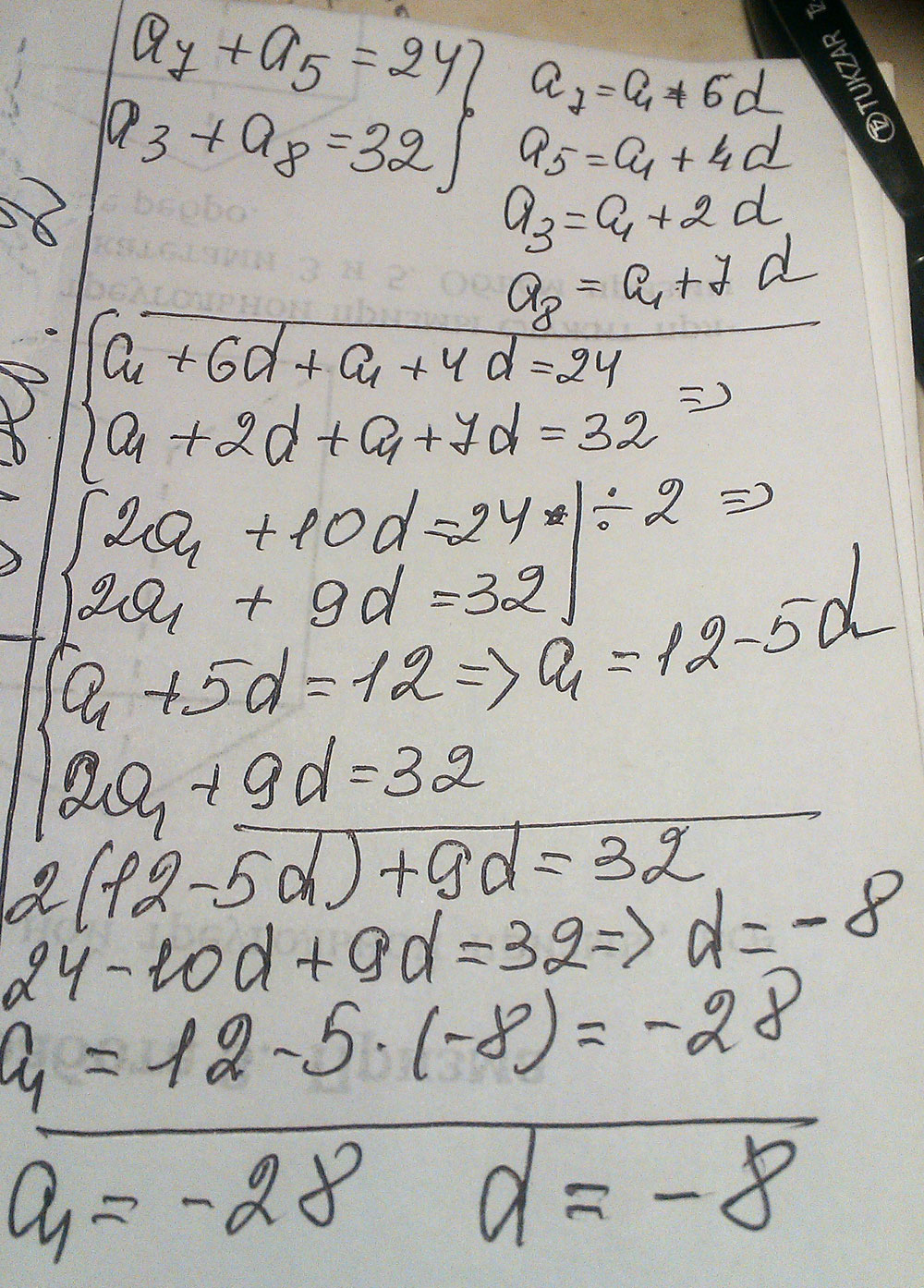найти первый член и разность прогрессии - страница 7
в арифметической прогрессии(An) сумма шестого и десятого членов равна 5,9 а разность двадцатого и четвёртого членов равна 2. найти двадцать пятый член этой прогрессии
Решение: сумма шестого и десятого членов:а₆ + а₁₀ = 5,9
а₁ + d(6 -1) + а₁ + d(10 -1) = 5,9
2а₁ + 5d + 9d = 5,9
2а₁ + 14d = 5,9 (1)
разность двадцатого и четвёртого членов:
а₂₀ - а₄ = 2
а₁ + d(20 -1) - а₁ - d(4 -1) = 2
19d - 3d = 2
16d = 2
d = 1/8
Подставим значение d в равенство (1):
2а₁ + 14 * 1/8 = 5,9
2а₁ + 14 * 1/8 = 5,9
2а₁ + 1,75 = 5,9
2а₁ = 4,15
а₁ = 4,15 : 2
а₁ =2,075
Найдем двадцать пятый член: а₂₅ = а₁ + d(25 -1) = 2,075 + 1/8 * 24 =
= 2,075 + 3 = 5,075
ОТВЕТ: а₂₅ = 5,075
В арифметической прогрессии 26 членов, и разность этой прогрессии равна 15. Сумма всех членов прогрессии в 5 раз больше, чем сумма членов, стоящих на нечетных местах. Найти первый член этой прогрессии.
Решение: Формула суммы первых n членов конечной арифметической прогрессии такова:
$$ S= \frac{( a_{1} + a_{n})*n}{2} = \frac{(2 a_{1}+(n-1)d)*n }{2} $$
где n - количество членов прогрессии, d - разность прогрессии.
для членов, стоящих на нечетных местах, разность уже будет равна не d, а 2d.
Отсюда составим уравнение:
$$ (2 a_{1} +375)*13=5* \frac{(2 a_{1}+360)*13 }{2} $$
домножим обе части на 2:
(2a1+375)*26=5*(2a1+360)*13
52a1+9750=130a1+23400
-78a1=13650
a1=-175 - искомый ответ
Сумма первых 6 членов арифметической прогрессии равна 9, а разность между 4-м и 2-м членами равна 0,4. Найти 1-й член этой прогрессии. Ответ 1. Нужен сам ход решения
Решение: //////////////////////////////////////////////////////////d = (a₄ - a₂) / 2 = 0.4/ 2 =0.2
S₆ = (a₁ + a₆) *6 /2
a₆ = a₁ + 5d = a₁ + 1
S₆ = (a₁ + a₁ + 1)*6 / 2 = 3 (2a₁ + 1) = 6a₁ + 3
6a₁ +3 =9
6a₁ = 6
a₁ = 1
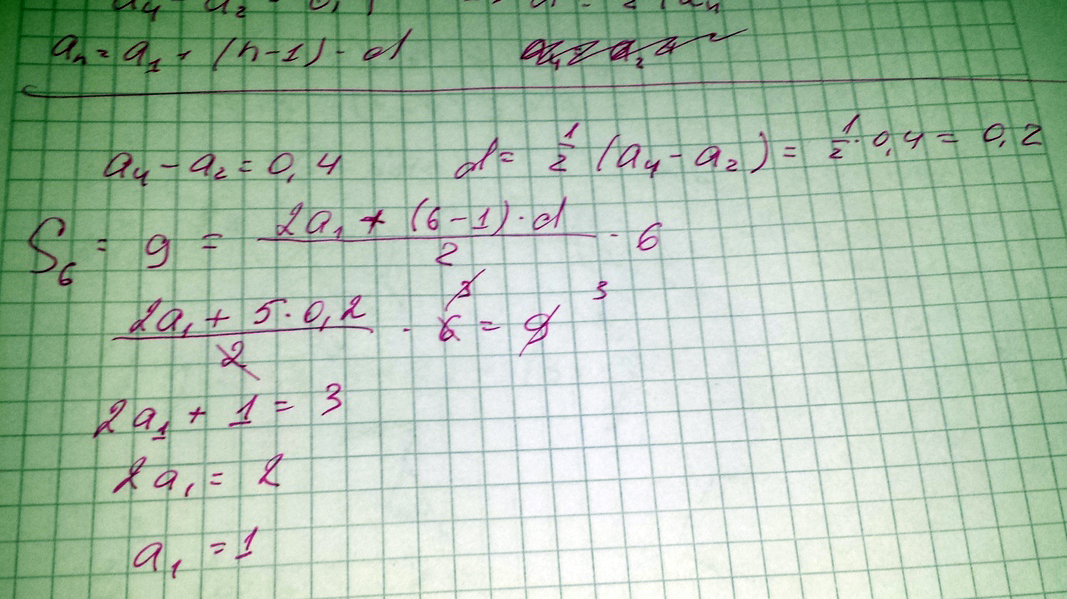
В арифметической прогрессии сумма седьмого и пятого членов равна 24, а сумма третьего и восьмого равна 32. найти разность арифметической прогрессии.
Решение:Седьмой член выражается формулой a7=a1+6*d, где d - искомая разность прогрессии. Пятый член a5=a1+4*d. По условию, a7+a5=2*a1+10*d=24. Аналогично a3=a1+2*d и a8=a1+7*d, тогда по условию a3+a8=2*a1+9*d=32. Получена система уравнений:
2*a1+10*d=24
2*a1+9*d=32.
Вычитая из первого уравнения второе, сразу находим d=24-32=-8.
Ответ: d=-8.
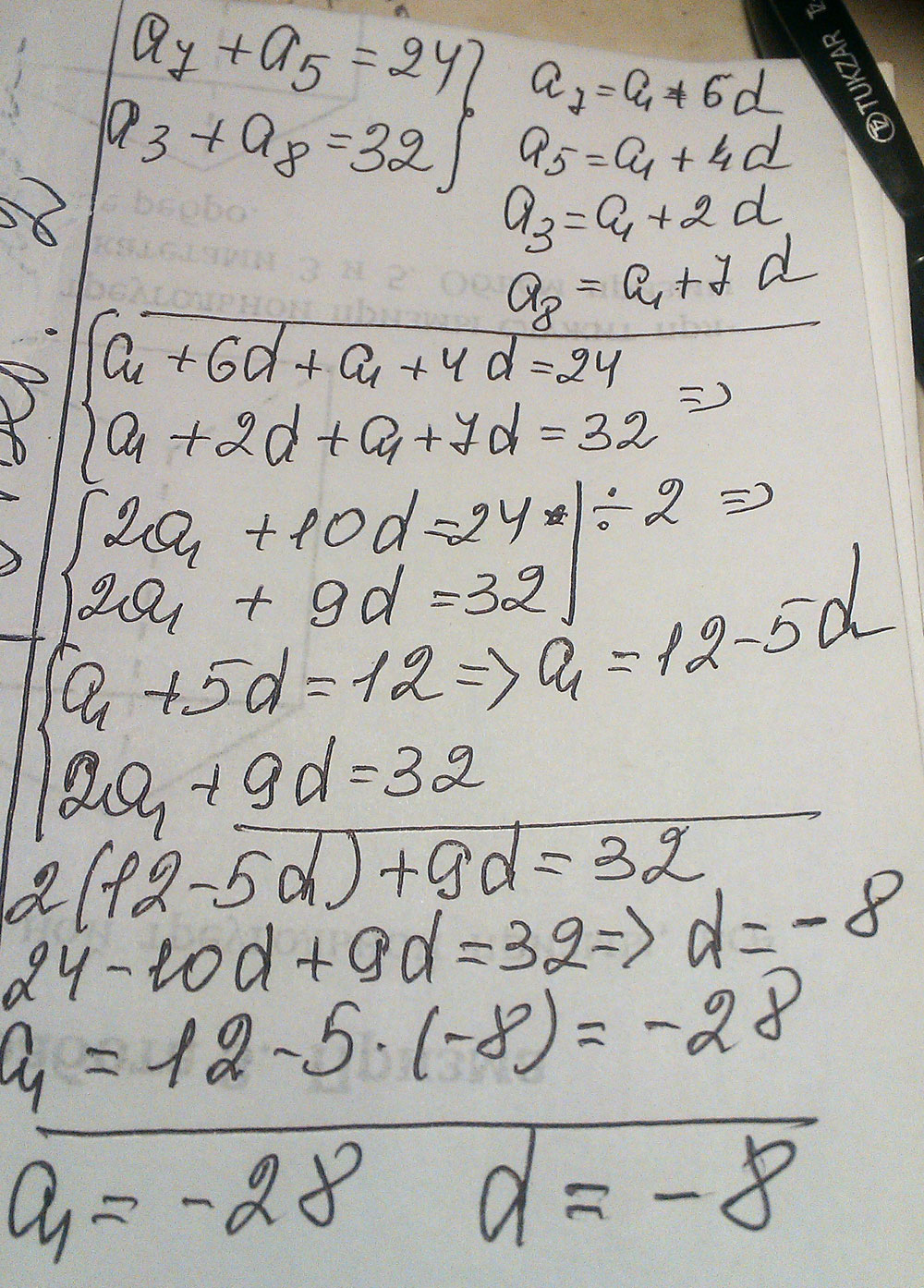
1) Сумма первых восьми членов арифметической прогрессии равна 64, а разность между 8-м и 3-м членами равна 10. Найти пятый член прогрессии.
2) Найти сумму всех натуральных чисел, каждое из которых кратное 11 и не превосходит по величине 1000.
3) Найти восьмой член геометрической прогрессии, если b4=200, q=0,1
Решение: S8=2a1+d(8-1)/2*8=(2a1+7d)*4=64
a8=a1+7d
a3=a1+2d => a8-a3=5d=10 d=2
64 =(2a1+7*2)*4 (/4) 16=2a1+14 2a1=16-14 2a1=2 a1=1
a5=a1+4d=1+4*2=9
3) b4=200 q=0.1 b8=b1*q^7
b4=b1*q^3 200=b1*0.1^3 b1=200/0.1^3=200*1000=2*10^5
b8=2*10^5*0.1^7=1*10^5*10^-7=2*10^-2=2/100=0.02
2) a1=11 d=11 Sn=2a1+d(n-1)/2*n Sn=1000 => 2000=22+11(n-1)*n 2000-22=11n^2-11n
11n^2-11n-1978=0 d=121+4*11*1978=87153 VD=295 n=11+295/22=13
корень приблизительно и nберем целую часть