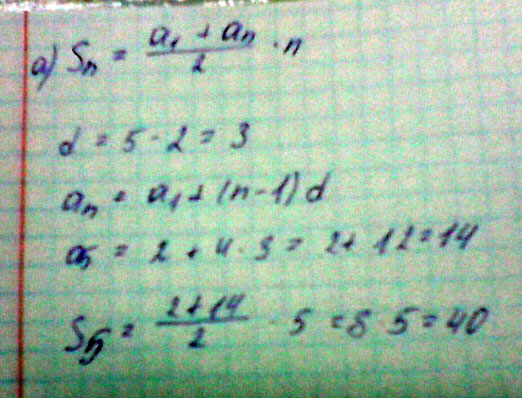прогрессия »

сумма первых членов арифметической прогрессии - страница 10

  • Найдите сумму первых пяти членов:
    а) арифметической прогрессии 2;5;8.
    б) геометрической прогрессии 1;3;9.


    Решение: Арифметическая:s=((2a1+d(n-1))/2)*n
    d=a2-a1=5-2=3
    d-разность
    a2=5
    a1=2
    s=((2*2+3(5-1))/2)*5=40
    n-количество членов прогрессии
    геометрическая:s=b1*(q^n-1)/q-1
    q=q2/q1=3/1=3
    s=1*(3^5-1)/5-1=60.5
    q-знаменатель
    n-кол-во членов прогрессии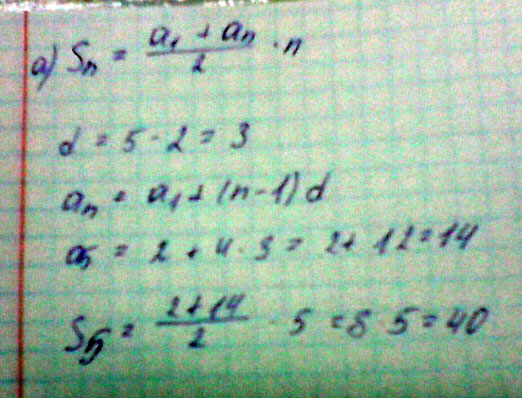

    Арифметическая s a d n- nd a -a - d-разностьa a s - n-количество членов прогрессиигеометрическая s b q n- q- q q q s - - . q-знаменательn-кол-во членов прогрессии...

  • 1) Найдите сумму первых десяти членов арифметической прогрессии (xn), если x2=-2,4 и d=1,2 2) Найдите двенадцатый член геометрической прогрессии(bn), если

    b2=-1\32

    b3=1\16


    Решение: 1) S10=( х1+х10):2*10

    х10=х1+9d

    х1=х2-d

    х1=-3,6

    х10=-3,6+9*1,2

    х10=7,2 

    S10= (-3,6+7,2)*5

    S10= 18

    2)Cначала найдем q

    q=b3/b2

    q= -2

    b12=b1*q11

    b1=b2/q 

    b1=-1/32 / -2

    b1=1/64 

    b12= 1/64*(-2)^11

    b12=-32 

  • Первый, второй и пятый члены арифметической прогрессии представляют собой первые три члена геометрической прогрессии. Если к первым двум членам этой геометрической прогрессии прибавить по 1, а от третьего отнять 3, то получатся первые три члена некоторой арифметической прогрессии. Найдите сумму первых ста членов исходной арифметической прогрессии.


    Решение:
    Пусть первый, второй и пятый члены исходной арифметической прогрессии

    а1 = х
    а2 = x + d
    а5 = x + 4d

    Они же - это первые три члена геометрической прогрессии:
    b1 = x, b2 = x + d, b2 = x + 4d,
    значит
    $$ \frac{x + d}{x} = \frac{x + 4d}{x + d} \\ (x + d)^{2} = x(x + 4d) \\ x^{2} + 2xd + d^{2} = x^{2} +4xd \\ d^{2} = 2xd \\ d = 2x $$  
    $$ x = \frac{d}{2} $$
    Из них получаем первые три члена другой арифметической прогрессии:

    с1 = b1+1  = x +1,
    с2 = b2+1 = x + d +1,
    с3 = b2 - 3 = x + 4d - 3  
    Тогда 
    $$ (x + d +1) - (x +1) = (x + 4d - 3) - (x + d +1) \\ x + d +1 - x - 1 = x + 4d - 3 - x - d - 1 \\ d = 3d - 4 \\ 2d = 4 \\ d = 2 $$
    Значит а1 = х = d/2 = 2/2 = 1.

    Тогда сумма первых ста членов исходной арифметической прогрессии равна:
    $$ S_{100} = \frac{2 a_{1}+99d }{2} *100 = \frac{2 *1+99*2 }{2} *100 = (1+99)*100 = \\ = 100*100 = 10000 $$

    Ответ: 10000.





  • Первый, второй и пятый члены арифметической прогрессии представляют собой первые три члена геометрической прогрессии. Если к первым двум членам этой
    геометрической прогрессии прибавить по 1, а от третьего отнять 3, то получатся первые три члена некоторой арифметической прогрессии. Найдите сумму первых ста членов исходной арифметической прогрессии.


    Решение: Так как члены представляют собой арифметическую прогрессию, то a2=a1+d, a5=a1+4d, где d - знаменатель арифметической прогрессии. Но так как эти же члены являются членами геометрической прогрессии, то a2=a1*q и a5=a1*q², где q - знаменатель геометрической прогрессии. По условию, a2+1=a1+1+d1, a5-3=a1+1+2d1, или a2=a1+d1, a5=a1+4+2d1. Из первого уравнения находим d1=d. Так как a5=a1+4d, то из второго уравнения следует уравнение 4d=4+2d, откуда d=2. Теперь, заменяя a2 на a1+2 и a5 на a1+8, получаем уравнения a1+2=a1*q, a1+8=a1*q². Из первого уравнения следует a1=2/(q-1). Подставляя это выражение во второе уравнение, приходим к квадратному уравнению q²-4q+3=0. Дискриминант D=(-4)²-4*1*3=4=2². Отсюда q=(4+2)/2=3 либо q=(4-2)/2=1. Но если q=1, то все члены геометрической прогрессии, а с ней и все члены исходной арифметической прогрессии, были бы равны, что было бы возможно лите при d=0. Но так как d=2≠0, то q≠1. Значит, q=3. Тогда a1=2/(3-1)=1, и искомая сумма S100=100*(a1+a100)/2=50*(a1+a100). Но a100=a1+99d=1+99*2=199, и тогда S100=50*(1+199)=10 000. Ответ: 10 000.  

  • 1. Найдите 18 член арифметической прогрессии если a1=7, d=4;
    2. Найдите сумму 16-ти первых членов арифметической прогрессии: -8; -4; 0.;
    3. Найдите сумму пятидесяти первых четных натуральных чисел;
    4. Найдите седьмой член геометрической прогрессии если b1=-25 и q=-1/5


    Решение: №1 а18=7+17*4=7+68=75
    №2 d=-4-(-8)=-4+8=4
    а16=-8+15*4=-8+60=-52
    S=(-8+52)/2 * 16=44/2 * 16=22*16=352
    №3 а1=2, d=2
    а50=2+2*49=2+98=100
    S=(2+100)/2 * 50=102/2 *50=51*50=2550
    №4 b7=-25* (-1/5)^6=-25/5^6=-1/5^4=-1/625

    3.
    2; 4; 6;.
    А₁=2
    А₂=4
    d=A₂-A₁=4-2=2
    A₅₀=A₁+49d=2+49*2=2+98=100
    S₅₀=(A₁+A₂)n =(2+100)*50=102*25=2550
      2 2
    Ответ: 2550

    4.
    b₇=b₁*q⁶=-25*(-1/5)⁶ =-5² * (1/5)⁶ = -5² * (5⁻¹)⁶ = -5² * 5⁻⁶ = -5⁻⁴ = -1/625
    Ответ: -1/625

<< < 8910 11 12 > >>