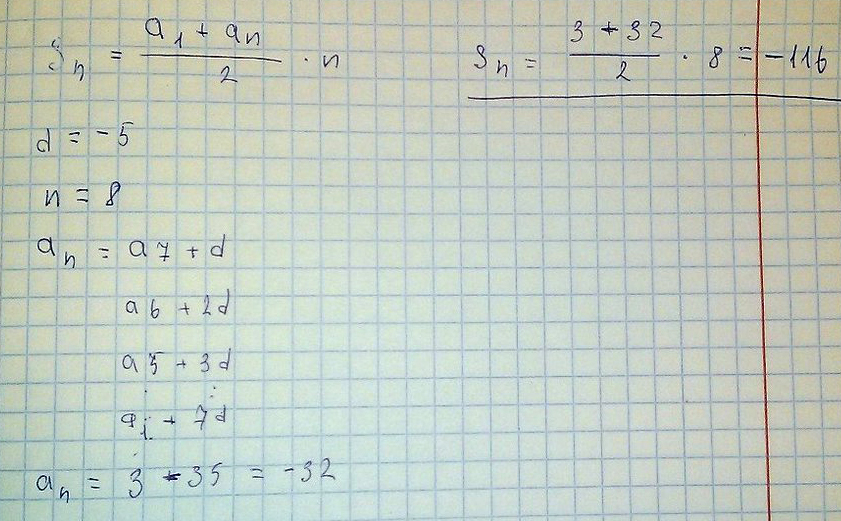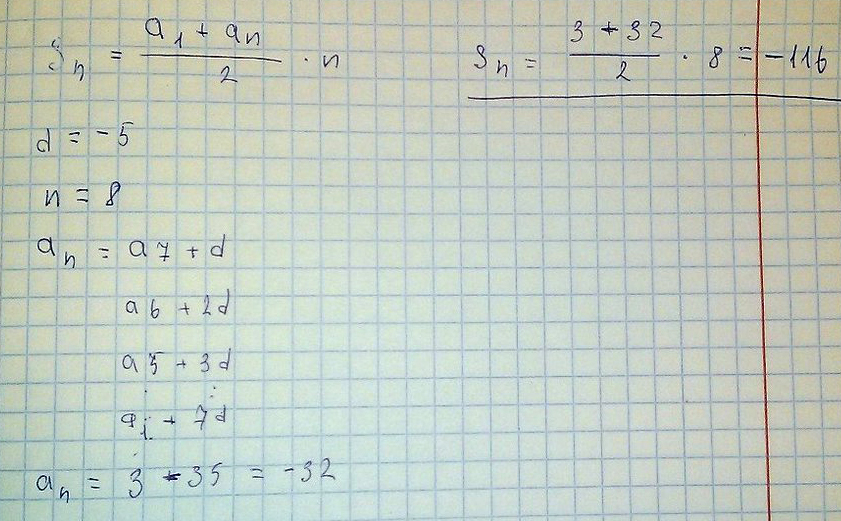прогрессия »
сумма первых членов арифметической прогрессии - страница 15
Дана арифметическая прогрессия: −4 ; −2 ; 0…. Найдите сумму первых десяти её членов.
Решение:
S= a1+an/2 и все умножить на n
S10= -4+10/2 *10
S10=4*10
S10=40
Рада была помочь:)формула S=a1+an(n это десятое число прогрессии) поделить эту сумму на 2 и умножить на n, подставляем: a1=-4 an=14,4+14/2 и умножить на 10=10/2*10=50 можно проверить если промсто по прогрессии взять эти числа и последовательно сложить
1) Дана арифметическая прогрессия -31; -27;.
а) Найдите 31-й член прогрессии.
б) Определите, входит ли в данную прогрессию число 41.
5. Найдите сумму 19 первых членов арифметической прогрессии, если известно, что a4+a8+a12+a16=112.
Решение: 1) a) An=A1+d(n-1)
d=A2-A1
d=-27-31=4
A31=-31+4(31-1)=89
б) Если 41 входит в последовательность, значит 41=-31+4(n-1), где n - натуральное число.
41=-31+4n-4
4n=41+31+4
n=19
41 - член этой прогрессии
2) сумма прогрессии Sn=((A1+An)/2)*n
A4+A8+A12+A16=112
A1+3d+A1+7d+A1+11d+A1+15d=112
4A1+36d=112
A1+9d=28
A19=A1+18d=A1+9d+9d
S19=((A1+(A1+9d+9d))/2)*19
S19=((A1+9d)*2)/2*19
S19=(A1+9d)*19
S19=28*19=532
1. Дана арифметическая прогрессия -8,4,0, Найдите сумму первых семи её членов.
(решение)
2 решите неравенство 20х^2-121<=0
(решение)
Решение: 1) а7 = а1+6d; d=-4+8=4
a7=-8+6*4=16
S7= (a1+a7)/2 *7 = 281) -8,4,0,4,8,12,16,
сумма = 28
2) 20x^2-121<=0
20x^2<=121
x^2<=121^20
x^2=6,05
x= +- корень квадратный из 6,05
так как x^2 коэфициент положительный ветви параболы вверх
рисуем прямую отмечаем минус корень квадратный из 6,05 до 0 и после 0 корень квадратный из 6,05
Ответ: [-корень квадратный из 6,05; корень квадратный из 6,05]Дана арифметическая прогрессия: 6; 10; 14; …. Найдите сумму первых пятидесяти её членов. Записаны первые три члена арифметической прогрессии: 20; 17; 14. Какое число стоит в этой арифметической прогрессии на 91-м месте?
Решение: Мы знаем три члена. Надо найти разность прогрессии.
$$ a_{1} =20 $$
$$ a_{2} =17 $$
Разность между ними составляет:
$$ d= a_{2} - a_{1} =17-20=-3 $$
Сумма считается по формуле
$$ S_{n} = \frac{2 a_{1}+( n-1)*d}{2} *n $$
$$ S_{50} = \frac{2*20+49*(-3)}{2} *50 = \frac{40-147}{2}*50=-107*25= -2675 $$
Формула n-ного члена считаеться по формуле
$$ a_{n}= a_{1} +d*(n-1) $$
$$ a_{91}=20+(-3)*(91-1)=20+(-3*90)=20-270=-250 $$
Дана арифметическая прогрессия 3;-2;-7;. Найдите сумму первых восьми её членов.
Решение: Формула арифметической прогрессии
a(n)=a(1)+d*(n-1)
первый член известен и равен 3
разность между соседними членами равна разности прогрессии (d)
для данной прогрессии d=-5
формула данной прогрессии a(n)=3-5*(n-1)
сумма n членов прогрессии равна полусумме крайних членов умноженной на n
a(1)=3
a(8)=3-5*7=-32
S(8)=(3-32)*4=(-29)*4=-116