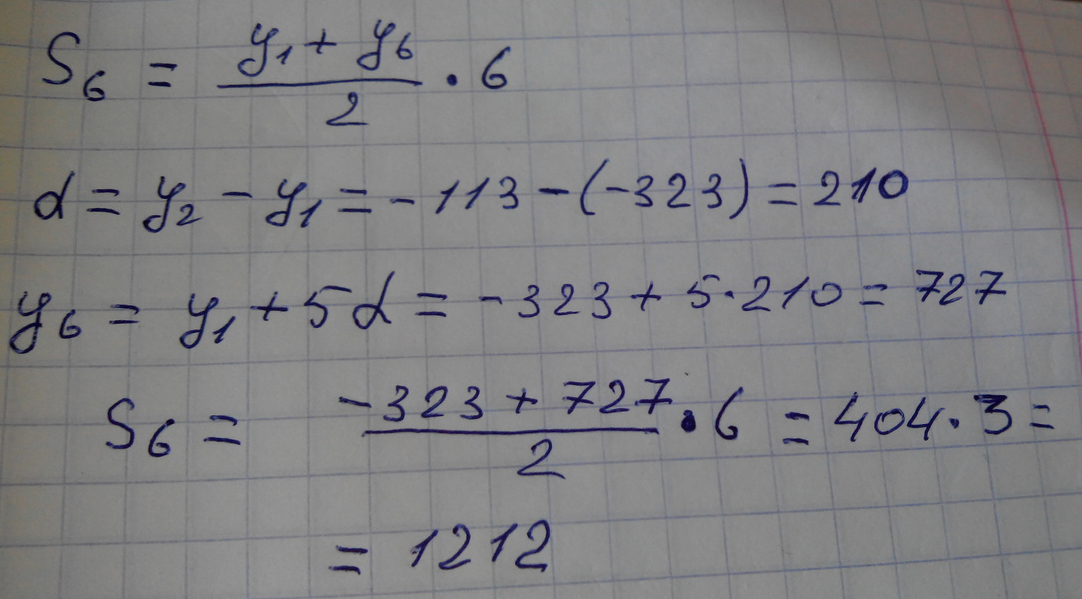сумма первых членов арифметической прогрессии - страница 17
Дана арифметическая прогрессия y1=−323,y2=−113,… Найдите сумму первых шести членов этой прогрессии.
Решение: С помощью y1 И y2 найдем d(разность ариф. прогрессии).
d=y2-y1=-113+323=210
Находим y6 для того, чтобы найти сумму первых шести членов этой прогрессии.
y6=y1+5d=y2+4d=-113+210*4=727
S6=((y1+y6)/2)*6=1212
Формула нахождения суммы ариф. прогрессии:
Sn = ((a1 + an)/2)*n, ответ 1212
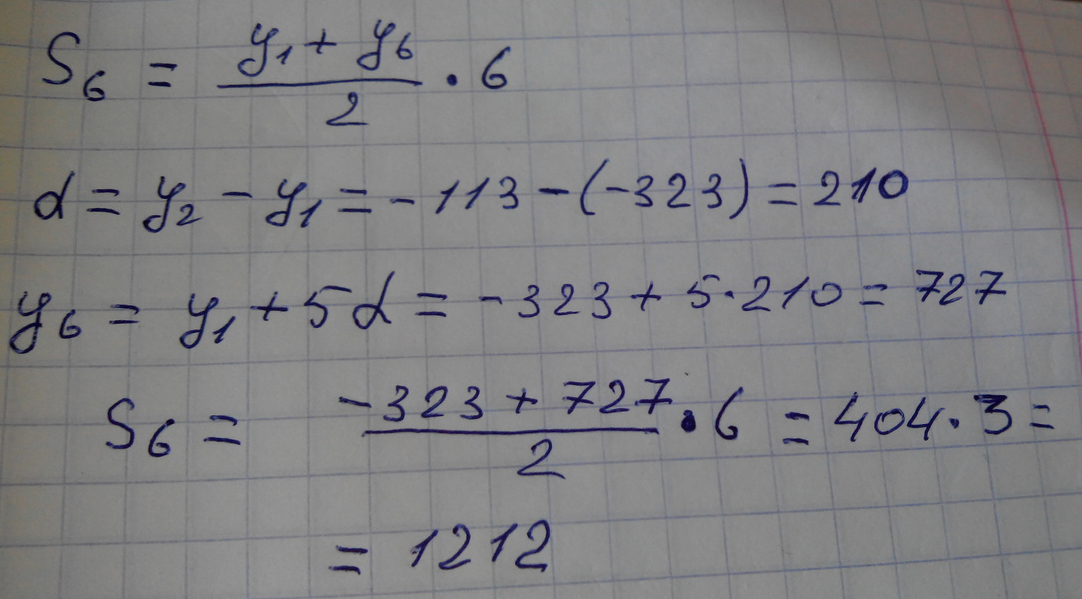
1. Дана арифметическая прогрессия -2,0,2,4.
Найдите сумму первых петнадцати ее членов.
2. из формулы s=at^2/2 выразите a
Решение: №1) Дано: -2,0,2,4. арифметическая прогрессияНайти: S14
Решение:
а1 = -2
d = a4-a3 = 4-2 = 2
Sn = ((2а1+d*(n-1)) / 2 ) *n
S14 = ((2*(-2)+2*(14-1)) / 2 ) *14 = 154
Ответ: S14 = 154.
№2)
s=at^2/2
а = (2 * s) / t ^ 2
Ускорение равно отношению удвоенного расстояния на квадрат времени.1) a1=-2 d=a2-a1=2
a15=a1+(n-1)*d a15= -2+(15-1)*2 a15=26
Sn=((a1+an)/2)*n S15=((-2+26)/2)*15 S15=180
1) В трапеции ABCD AB=BC=CD. Точки K,L,M и N - середины сторон трапеции. Найдите наибольший угол четырёхугольника KLMN, если угол BAD равен 40∘. Ответ дайте в градусах.
2) В стакане с ручками стоят 6 ручек, которые еще пишут, и 4 ручки, которые уже не пишут. Случайно выбирается одна ручка, с какой вероятностью она пишет?
3) Дана арифметическая прогрессия y1=−323,y2=−113,… Найдите сумму первых шести членов этой прогрессии.
4) Диагонали ромба равны 24 и 7,5. Найдите его площадь.
5) Какие из следующих утверждений верны? В любой прямоугольный треугольник можно вписать окружность. Каждая сторона треугольника больше суммы двух других сторон. В треугольнике ABC угол A равен 43∘, угол C равен 72∘,AC - меньшая сторона. Медиана, проведенная к гипотенузе прямоугольного треугольника, равна половине гипотенузы. Любые два равнобедренных треугольника подобны.
Решение: К задаче №1.1) KB=BL (так как AB=BC и точки K и L - середины)
2) угол ABC=140 градусов (т. к. сумма углов при боковой стороне трапеции 180) (180-40=140)
3) угол KLB=углу BKL=20 градусов (свойство равнобедренного треугольника) (180-140)/2=20
4) треугольник LCM=треугольнику KBL (по 1-му признаку и п.1)
5) Наибольший угол KLMN равен 180-2*20=140
Этот четырёхугольник является ромбом, т. к. KL=LM=MN=NA (это средние линии треугольников ABC и ADC)
К задаче №3.
1) найдём d=y2-y1=-113+323=210
2) По формуле суммы n членов арифметической прогрессии:
S(6)=6*(2*(-323)+210*5)/2=1212
К задаче №4.
1) Воспользуйтесь формулой S ромба=(1/2)*d1*d2, получим 24*7,5/2=90
К задаче №5.
Верными являются утверждения №1 и 4
Дана арифметическая прогрессия ( Cn ) c5 = 27 c27 = 60 найдите сумму первых 8 членов прогрессии
Решение: Формула общего члена арифметической прогрессии:
$$ c_n=c_1+(n-1)d $$
$$ c_5=c_1+4d, \\ 27=c_1+4d \\ c_{27}=c_1+26d, \\ 60=c_1+26d, $$
Осталось решить систему двух уравнений с двумя переменными $$ c_1 $$ и d
$$ \left \{ {{c_1+4d=27} \atop {c_1+26d=60}} \right. $$
Вычитаем из второго уравнения первое:
22d=33
d=1,5
c₁=27-4d=27-4·1,5=27-6=21
c₈=c₁+7d=21+7·1,5=31,5
$$ S_8= \frac{c_1+c_8}{2}\cdot n= \frac{21+31,5}{2}\cdot 8=210 $$
Дана арифметическая прогрессия аn. известно что а1+а4+а13 =-27 Найдите сумму первых 11 членов?
Решение: Мы знаем формулу суммы арифметической прогрессии вида$$ S_{n}=\frac{2a_{1}+d(n-1)}{2}*n $$
У нас же с данным значением найти сумму 11 она будет выглядеть так
$$ S_{11}=\frac{2a_{1}+10d}{2}*11 $$
Сл-но для нас надо найти главное значение вверху дроби. Я сделала так
Представим а1+а4+а13 =-27 так а1+а1+3d+а1+12d=-27
Выносим общий множитель
3(а1+5d)=-27
а1+5d=-9
Теперь полученное значение а1+5d=-9 прибавляем к прошлой сумме 3а1+15d=-27 и у нас получается
4a1+20d=-36 Можно сказать вот мы и нашли то чт нам нужно. Делим получившееся выражения на 2
4a1+20d=-36 | :2
2a1+10d=-18 Вот что мы и искали. Ну а теперь нам легко найти сумму
$$ S_{11}=\frac{2a_{1}+10d}{2}*11 $$
В эту формулу подставляем найденные значения и получаем
$$ S_{11}=\frac{-18}{2}*11=-9*11=-99 $$