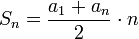сумма первых членов арифметической прогрессии - страница 18
Тема: Формула суммы n первых членов арифметической прогрессии.
Из пункта A выехал грузовой автомобиль и двигался со скоростью 40 км/ч. Одновременно в том же направлении из пункта В отправился легковой автомобиль, который в первый час прошёл 50 км, а в каждый следующий проходил на 5 км больше, чем в предыдущий. Через сколько часов легковой автомобиль догонит грузовой, если известно, что расстояние от пункта B до пункта А равно 135?
Решение: Скорость грузового - 40, легкового - 50за первый час легковой догонит грузового на 50-40=10 км
за второй на 10+(55-40)=25 км. и тд. каждый час все больше.
Положим, что первый член равен 10, тогда второй - 15, третий 20 и т. д.
Сумма членов прогрессии 10,15,20,25. должна равнятся 135
Сумма АП равна $$ S=\frac{a1+an}{2}n $$, но т. к. последний член не известен выразим an через a1 и n: $$ a_{n}=a_{1}+(n-1)d $$ и формулу суммы можно переписать в виде $$ S=\frac{a_{1}+a_{1}+(n-1)d}{2}n=\frac{2a_{1}+(n-1)d}{2}n $$
Подставим известные данные
$$ 135=\frac{2*10+(n-1)5}{2}n $$
$$ 135=10n+\frac{5n^{2}}{2}-\frac{5n}{2}-135=0 $$
Решим квадратное уравнение
$$ 5n^{2}+15n-270=0 $$
Положительный корень x = 6 показывает количество членов Ап. т. е. часов за которые легковой догонит грузового
найдите сумму первых восьми членов арифметической прогрессии
а) -23,20
и объясните почему именно та или иная формула.
Решение: -23 -20 -17 -14 -11 -8 -5 -2 Sn=(a1+an/2)*n=(-23+(-2)/2)*6=-75Sn Сумма первых членов арифметической прогрессии
a1первый член прогрессии
an член с номером n
n— количество суммируемых членов
1) а1=-23 d=-20+23=3
2) по формуле н-ого члена
а(n)=а1+(n-1)d
а8= -23+(8-1)3=-2
3) по формуле S(n)=((а1+аn)/2)*8
S8=((-23-2)/2)*8=100
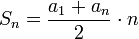
Найдите сумму первых ста членов арифметической прогрессии (An) если известно что А1=73, d=-1
Решение: Нужно найти S100. Берем основную формулу 2A1+(n-1)×d/2 *nn- индекс, допустим нужно найти сумму 50 членов, тогда n=50, если 10 то n=10
Подставляем
S₁₀₀=73+(100-1)×(-1)/2 ×100=-1450
Для нахождения членов арифметической прогрессии, при известном первом члене и d, нужно к каждому последующему члену добавлять число d. Тоесть, для нахождения второго члена нужно A1+d=A2
A3=A2+d
A4=A3+d
и так далее.
Сумма первых 8ми членов арифметической прогрессии равна 88, сумма 3го и5го членов равна 18, найти 7 член прогрессии
Решение: $$ S_{n}= \frac{2a_1+(n-1)d}{2} *n $$
$$ a_n=a_1+(n-1)d $$
$$ S_8= \frac{2a_1+7d}{2} *8 $$
$$ a_3=a_1+2d $$
$$ a_5=a_1+4d $$
$$ a_3+a_5=a_1+2d+a_1+4d=2a_1+6d $$
$$ \left \{ {{ \frac{2a_1+7d}{2}*8=88 } \atop {2a_1+6d=18}} \right. $$
$$ \left \{ {{ \frac{2a_1+7d}{2}=11 } \atop {2a_1+6d=18}} \right. $$
$$ \left \{ {{ {2a_1+7d}=22 } \atop {2a_1+6d=18}} \right. $$
$$ \left \{ {{ {d}=22-18 } \atop {2a_1+6d=18}} \right. $$
$$ \left \{ {{ {d}=4 } \atop {a_1+3d=9}} \right. $$
$$ \left \{ {{ {d}=4 } \atop {a_1+3*4=9}} \right. $$
$$ \left \{ {{ {d}=4 } \atop {a_1=-3}} \right. $$
$$ a_7=a_1+6d=-3+6*4=-3+24=21 $$
Ответ: $$ 21 $$1. Известно, что в арифметической прогрессии сумма ее первых 11 членов равна 22. Чему равна сумма а4+2а6+а8.
2. В арифметической прогрессии сумма трех членов равна 30, а6-а4=-4 и аn=-10. Чему равно n?
Решение: 1. s=((2a1+10d) /2) *112a1+10d = 1
a1+3d+2a1+10d+a1+7d = 2(a1+10d)=2
2/ 30=2a1+2d /2 *3
a1+5d-a1-3d=-4
2d=-4
d=-2
30=2a1-4 /2 *3
2a1=24
a1=12
an = a1+d(n-1)
-10= 12+(-2)(n-1)
n-1=11
n=12
2. если а6-а4=-4, то d=-2
S3=(а1+аn)/2 * n, 30=(a1-10)/2*3, 30=(3a1-30)/2, 60=3a1-30, 3a1=90, a1=30
an=a1+(n-1)d,10=30+(n-1)*(-2),10=30-2n+2, 2n=2+30+10, 2n=42,
n=21
1. Sn=(a1+an)/2 * n, 22=(a1+a11)/2 * 11, 22=(11a1+11a11)/2, 44=11a1+11a11, 4=a1+a11.
В эту формулу подставляем наши данные :
$$ a_{1+p}+a_{n-p}=a_{1}+a_{n} $$
получаем а4+а8=а1+а11 б а4+а8=4
и 2а6=а1+а11, 2а6=4
а4+2а6+а8 - (а4+а8)+2а6=4+4=8