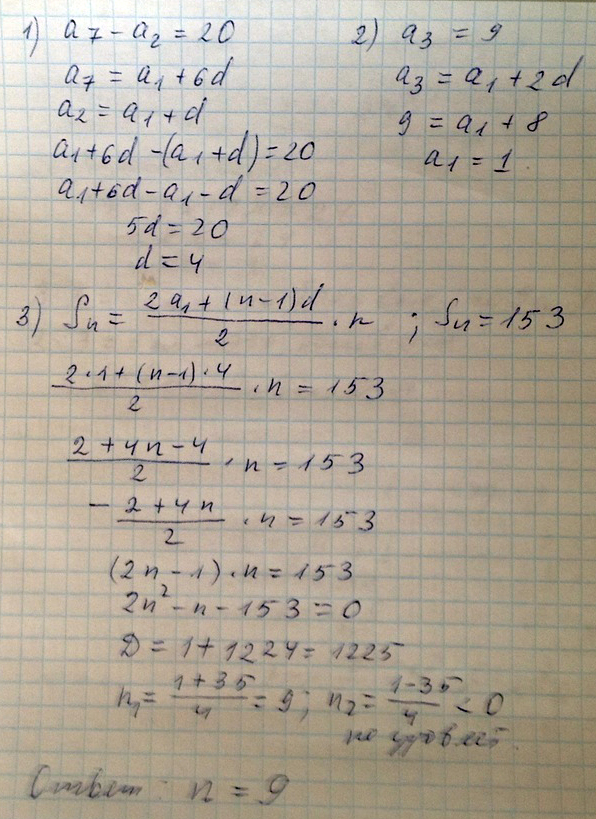сумма первых членов арифметической прогрессии - страница 24
Сумма первогои пятого членов арифметической прогрессии равна 5\3, а произведение третьего и четвертого её членов равно 65\72. Найти сумму первых 17 членов этой прогрессии.
Решение: сумма первого и пятого =a1+a1+4d=2a1+4d=5/3=>a1+2d=5/6произведение третьего и четвертого=(a1+2d)(a1+3d)=65/72
подставляем a1+2d=5/6 и получаем
(a1+3d)*5/6=65/72
a1+3d=13/12
a1+2d=5/6
Вычитаем из первого второе и получаем:
d=13/12-5/6=1/4=>a1=13/12-3/4=1/3
S17=(2a1+16d)/2*17=(2/3+4)/2*17=7*17/3=119/3=39 2/3
Пусть первый член прогрессии равен А, а разность - В. Выразим интересующие нас члены прогрессии через эти величины
а₁ + а₅ = А + А + 4 * В = 2 * А + 4 * В = 2 * (А + 2 * В) = 2 * а₃ = 5/3
Следовательно а₃ = 5/6
a₃ * a₄ = 5/6 * a₄ = 65/72, поэтому а₄ = 13/12
Итак В = а₄ - а₃ = 13/12 - 5/6 = 1/4
A = a₃ - 2 * B = 5/6 - 1/2 = 1/3
2 * A + 16 * B 17 119
Тогда S₁₇ = - * 17 = 17 * A + 136 * B = - + 34 = -
2 3 3
Сумма первых n членов арифметической прогрессии равна 153. Найти n если a3=9 и a7-а2=20
Решение: a3=a1+2da7=a1+6d
a2=a1+d
Система:
a1+2d=9
a1+6d-a1-d=20
a1+2d=9
5d=20 |:5
d=4
a1=1
2a1+(n-1)d
Sn=_________ *n
2
2+(n-1)4n
153=_______
2
2n^2-n-153=0
D=1225
n1=9
n2=-8,5 - не соответствует условию задачи.
n=9
Ответ:9
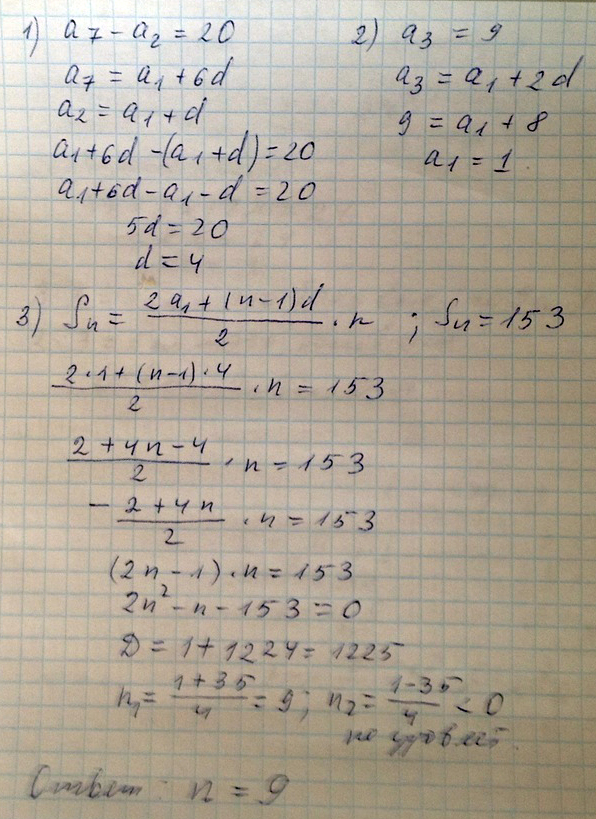
Сумма первых трех чисел арифметической прогрессии равна 222. Второй член в 5 раз больше первого члена арифметической прогрессии. Найдите первый член.
Решение: A₁ + a₂ + a₃ = 222 сумма первых трех чисел арифметической прогрессии
a₂ = 5a₁
a₂ - a₁ = a₃ - a₂
2a₂ = a₃ + a₁
a₂ + 2a₂ = a₁ + a₂ + a₃
3a₂ = 222
a₂ = 74
74 = 5a₁
a₁ = 74/5 = 14,8
проверка:
a₁ = 14,8
a₂ = 74
d = 74 - 14,8 = 59,2
a₃ = a₂ + d = 74 + 59,2 = 133,2
a₁ + a₂ + a₃ = 14,8 + 74 + 133,2 = 222
Сумма первых трех членов арифметической прогрессии равна 15. Если к этим членам соответственно прибавить 1; 3 и 9 то получатся первые три члена возрастающей геометрической прогрессии. Найдите первые семь членов этой геометрической прогрессии.
Решение: Согласно условию пусть а1, а2 и а3 - члены арифм. прогрессии. Тогда (а1+1), (а2+3) и (а3+9) - члены геом прогрессии.
Получим систему:
$$ \begin{cases} a_1+a_2+a_3=15 \\ (a_2+3)^2=(a_1+1)(a_3+9) \end{cases}\\ \begin{cases} a_1+a_1+d+a_1+2d=15 \\ (a_2+3)^2=(a_1+1)(a_3+9) \end{cases}\\ \begin{cases} 3a_1+3d=15 \\ (a_2+3)^2=(a_1+1)(a_3+9) \end{cases}\\ \begin{cases} a_1+d=5 \\ (a_1+d+3)^2=(a_1+1)(a_1+d+d+9) \end{cases}\\ \begin{cases} a_1=5-d \\ (5+3)^2=(5-d+1)(5+d+9) \end{cases}\\ $$
$$ \begin{cases} a_1=5-d \\ 64=(6-d)(14+d) \end{cases}\\ d^2+8d-20=0 $$
d = 10 или d = -2
При d = 10 получим арифметическую прогрессию 15; 5; -5.
Соответствующая ей геом. прогрессия есть 16; 8; 4 - не является возрастающей.
Значит, d = -2 - разность искомой арифм. прогрессии.
Соответствующая ей геом. прогрессия есть 4; 8; 16 - является возрастающей.
Итак:
$$ b_1=4,\ b_2=8,\ b_3=16,\ b_4=32,\ b_5=64,\ b_6=128,\ b_7=256. $$
В арифметической прогрессии сумма 1 и 6 членов равна 11, а сумма второго и четвертого членов равна 10. Найти сумму первых шести членов этой прогрессии
Решение: 1способ) а1+а6=а2+а5=а3+а4s6=3*(a1+a6)
s=33
2способ)
a2=a1+d
a4=a1+3d
a6=a1+5d
следывательно а1+а6=2а1+5d=11
a2+a4=2a1+4d=10
следывательно d=1
а1=3
s=33
Вот посмотри. и реши. удачи