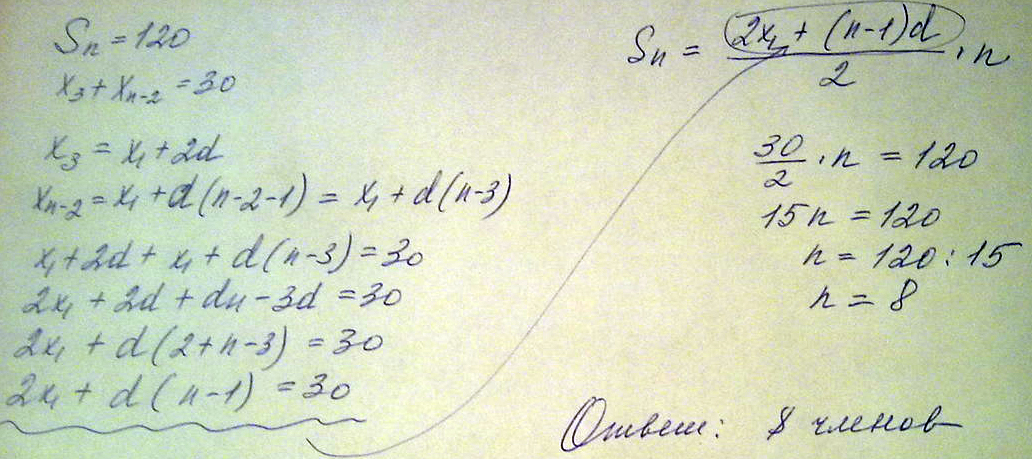сумма первых членов арифметической прогрессии - страница 28
Найти сумму четырех первых членов геометрической прогрессии, такой что её первые три члена, сумма которых равна 148/9 являются одновременно первым, четвёртым и восьмым членами арифметической прогрессии
Решение: По условию задачи
b₁=a₁
b₂=a₄
b₃=a₈
и
b₁+b₂+b₃=148/9
Основное характеристическое свойство геометрической прогрессии
b₂²=b¹·b³
По формуле общего члена арифметической прогрессии
а₄=а₁+3d
a₈=a₁+7d
Подставляем вместо b₁; b₂; b₃
а₁; a₄; a₈, выраженные через a₁ и d.
Получаем систему двух уравнений с двумя неизвестными a₁ и d.
{a₁+a₁+3d+a₁+7d=148/9
{(a₁+3d)²=a₁·(a₁+7d)
{3a₁+10d=148/9
{a₁=9d
3·9d+10d=148/9
37d=148/9
d=4/9
a₁=4
b₁=a₁=4
b₂=a₄=a₁+3d=4+3·(4/9)=4+(4/3)=16/3
q=b₂/b₁=(16/3):4=4/3
b₄=b₁·q³=4·(4/3)³=64/27
S₄=S₃+b₄=(148/9)+(64/27)=(148·3+64)/27=508/27
О т в е т. 508/27
1. Сколько отрицательных членов содержит арифметическая прогрессия -37,33,29.(нужно полное решение)
2. Сколько надо взять членов арифметической прогрессии 8,12,16, чтобы их сумма была равна 260?
3. среднее арифметическое двух чисел равно 2 1/5, причем 1/6 первого числа =1/4 второго числа. Найдите эти числа.
Решение: 1) Найдём d:d=-33-(-37)=5
тогда
$$ a_{1}+(n-1)*d<0\\-37+(n-1)*5<0\\5n<37+5\\5n<42\\x<8\frac{2}{5} $$
Следовательно отрицательных чисел 8.
2)$$ S_{n}=\frac{2a_{1}+(n-1)*d}{2} $$
Sn=260;
a1=8
d=12-8=4
$$ \frac{a_{n}+a_{k}}{2}=2\frac{1}{5}\\\frac{1}{5}a_{n}=\frac{1}{4}a_{k}\\a_{n}=\frac{5*a_{k}}{4}\\\frac{\frac{5a_{k}}{4}+a_{k}}{2}=2\frac{1}{5}\\\frac{9a_{k}}{4*2}=\frac{11}{5}\\45a_{k}=88\\a_{k}=\frac{88}{45}\\a_{n}+\frac{88}{55}=\frac{22}{5}\\a_{n}=\frac{22}{5}-\frac{88}{55}\\a_{n}=\frac{242-88}{55}\a_{n}=\frac{154}{55} $$
1. Из городов А и В навстречу друг другу одновременно вышли два товарных поезда. Они двигались без остановки, встретились через 24 часа после начала движения и продолжили свой путь, причём первый поезд прибыл в пункт В на 20 часов позднее, чем второй поезд прибыл в А. Сколько времени был в пути первый поезд?
2. Три Различных числа a,b,c, сумма которых равна 124, являются тремя последовательными членами геометрической прогрессии. Одновременно эти три числа a,b,c - являются соответственно третьим, тринадцатым и пятнадцатым членами арифметической прогрессии. Найдите числа a,b,c.
Решение: 1)
Для условности примем весь путь за 1 ! тогда по условию время до встречи одинаковое, пусть скорости их равны х и у тогда
$$ 24x+24y=1\\ \frac{1}{x}-\frac{1}{y}=20\\ \\ x=\frac{1}{24}-y\\ \frac{1}{\frac{1}{24}-y} - \frac{1}{y}=20\\ \frac{24}{1-24y} - \frac{1}{y}=20\\ 24y-(1-24y)=20y(1-24y)\\ 48y-1=20y-480y^2\\ y=\frac{1}{40}\\ x=\frac{1}{60} $$
то есть за 60 часов проехал !
2) $$ \frac{b}{a}=\frac{c}{b}\\ a_{1}+2d=a\\ a_{1}+12d=b\\ a_{1}+14d=c\\ \\ \frac{a_{1}+12d}{a_{1}+2d} =\frac{a_{1}+14d}{a_{1}+12d}\\ 3a_{1}+28d=124\\ \\ a_{1}=116\\ d=-8\\ a=4\\ b=20\\ c=100 $$Сумма первых n членов арифметической прогрессии (xn) равна 120 сколько первых членов в этой прогрессии если x3+xn-2 =30
Решение: -$$ S_n=120;x_3+x_{n-2}=30;\\\\x_n=x_1+(n-1)*d;\\\\x_1+x_n=x_1+x_1+(n-1)*d=\\=x_1+x_1+(n-2-1+3-1)*d=\\=x_1+(3-1)*d+x_1+(n-2-1)*d=x_3+x_{n-2}=30;\\\\S_n=\frac{x_1+x_2}{2}*n=120;\\\\\frac{30}{2}*n=120;\\\\15n=120;\\\=120:15=8 $$
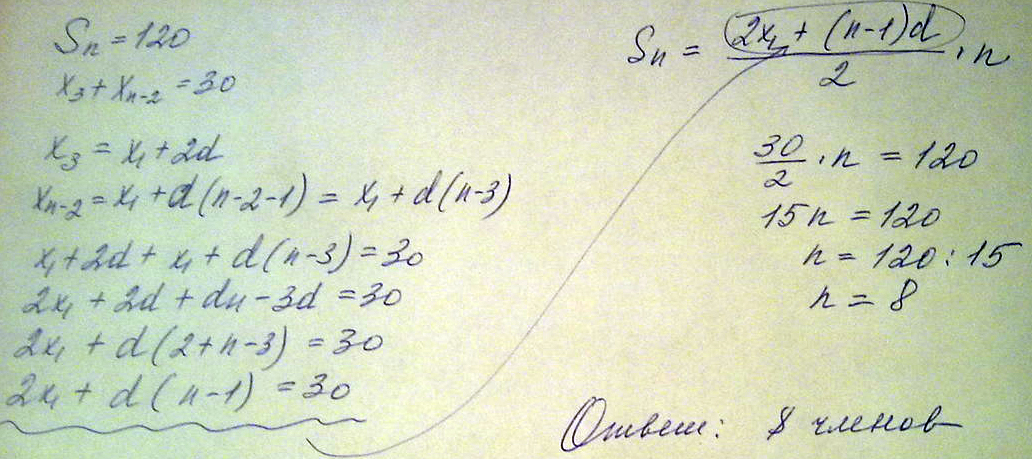
Сумма восьмого и тринадцатого членов арифметической прогрессии равна 3,5. Найдите сумму первых двадцати членов прогрессии
Решение: а8 + а13 = 3.5S20 -
аn = a1 + d(n -1) \\\\\ где n - эта член арифметической прогресси
a8 = a1 + 7d
a13 = a1 + 12d
S = ((2a + d(n - 1))/2)*n
а8 + а13 = 3.5
(a1 + 7d) + (a1 + 12d) = 3,5
2a1 + 19d = 3,5
2a1 = 3,5 - 19d
S = ((2a + d(n - 1))/2)*n
S20 = (((3,5 - 19d) + d(20 - 1))/2)*20
S20 = ((3,5 - 19d + 19d)/2)*20
S20 = ((3,5)/2)*20
S20 = 3,5*20/2
S20 = 3,5*10
S20 = 35
Ответ: сумма двадцати первых членов арифметической прогресси равна 35.