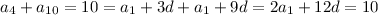прогрессия »
сумма первых членов арифметической прогрессии - страница 29
Сумма первого и четвертого членов арифметической прогрессий равна 2, а ее 5 член больше третьего на 4. Найдите сумму 10 ее первых
Решение: первый член А, четвёртый А+3Х, пятый А+4х, третий А+2х
получаем уравнения :
А+А+3х=2
А+4х=А+2х+4
из второго получаем, что 2х=4, х=2
первый член А=-2
подставляем в формулу суммы прогрессии
(А1+А10)*10/2=(-2+-2+9*2)*10/2=70Первый член прогрессии=А
Третий=А+2х
Четвертый=А+3х
Пятый=А+4х
А+А+3х=2
А+4х=А+2х+4
2х=4
х=2
А=2
(А1+А10)*10/2=70
Сумма восьмого и шестого членов арифметической прогрессии равна 16, а проиведение второго и двенадцатого равно -36. Найдите раность и первый член прогрессии
Решение: {a₈+a₆=16
{a₂ * a₁₂= -36
a₈=a₁+7d
a₆=a₁+5d
a₂=a₁+d
a₁₂=a₁+11d
{a₁+7d+a₁+5d=16
{(a₁+d)*(a₁+11d)= -36
{2a₁+12d=16
{a₁² + a₁d+11a₁d+11d²= -36
{a₁+6d=8
{a₁² + 12a₁d + 11d² = -36
a₁=8-6d
(8-6d)² + 12d(8-6d)+11d²= -36
64-96d+36d²+96d-72d²+11d²= -36
-25d²= -36-64
-25d²= -100
d² = 4
d₁=2
d₂= -2
При d=2
a₁=8-6*2= 8-12= -4
При d= -2
a₁=8-6*(-2)=8+12=20
Ответ: a₁=20 d= -2;
a₁= -4 d=2Сумма 5 и 13 членов арифметической прогрессии равна 10. найдите сумму первых 17 ее членов.
Решение: А5+а13=10
а5=а1+4d
a13=a1+12d
a5+a13=2*a1+16*d
S17=(2*a1+16*d)*17/2=(a5+a13)*17/2=10*17/2=85
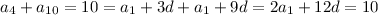
Сумма первого и пятого членов арифметической прогрессии равна 4, а произведение этих же чисел равно -32. Найдите третий член прогрессии.
Решение: A₅ = a₁ + d(5 - 1) = a₁ + 4d.
По первому условию:
a₁ + a₁ + 4d = 4,
2a₁ + 4d = 4.
a₁ + 2d = 2. Отсюда a₁ = 2 - 2d.
По второму условию:
a₁ * (a₁ + 4d) = -32.
Заменим a₁ на 2 - 2d:
(2 - 2d)(2 - 2d + 4d) = -32,
(2 - 2d)(2 + 2d) = -32,
4 - 4d² = -32 сократим на 4,
1 - d² = -8,
d² = 1 + 8 = 9,
d = √9 = +-3. Примем первое значение d = 3.
a₁ = 2 - 2*3 = 2 - 6 = -4,
a₅ = a₁ + 4d = -4 + 4*3 = -4 + 12 = 8.
Проверяем условие: а₁ + а₅ = -4 + 8 = 4,
а₁*а₅ = (-4)*8 = -32.
Примем второе значение d = -3.
a₁ = 2 - 2*(-3) = 2 + 6 = 8,
a₅ = a₁ + 4d = 8 + 4*(-3) = 8 - 12 = -4.
Проверяем условие: а₁ + а₅ = 8 - 4 = 4,
а₁*а₅ = 8*(-4) = -32.
Оба варианта верны, значит задача имеет два варианта ответа.
Третий член прогрессии равен:
по первому варианту:
a₃ = a₁ + d(3 - 1) = a₁ + 2d
а₃ = -4 + 2*3 = -4 + 6 = 2.
По второму варианту:
а₃ = 8 +2*(-3) = 8 - 6 = 2.
В обоих вариантах значения третьего члена прогрессии совпадают.
Сумма ста тридцати первых членов арифметической прогрессии равна сумме ее первых восьмидесяти членов. найдите сумму первых двухсот десяти членов этой прогрессии.
Решение: Рассмотрим общий случайSn=(2a1+d(n-1))*n/2
Sk=(2a1+d(k-1))*k/2
(2a1+(n-1)d)*n/2=(2a1+(k-1)d)*k/2
2a1(n-k)=k(k-1)d-n(n-1)d
a1=d(k^2-k-n^2+n)/2(n-k)
a1=d(-(n^2-k^2)+n-k)/2(n-k)
a1=d(-n-k+1)/2
a1=-d(n+k-1)/2
S_(n+k)=(2a1+d(n+k-1))(n+k)/2
d(n+k-1)=-2a1
S_(n+k)=(2a1-2a1))(n+k)/2=0
Т. е. мы доказали, что для любых n и k, если сумма n первых членов прогрессии равна сумме k первых членов прогрессии, сумма n+k первых членов прогрессии всегда равна 0.
Значит S210=0.
100a1=d(6400-80-16900+130)
100a1=-10450d
a1=-104,5d
S210=(2a1+d(210-1))*210/2=420a1+21945d=-(43890+21945)d=-21945d
S130=(-209d+129d)130/2=-80d*65=-5200d
S80=(-209d+79d)*40=-130d*40=