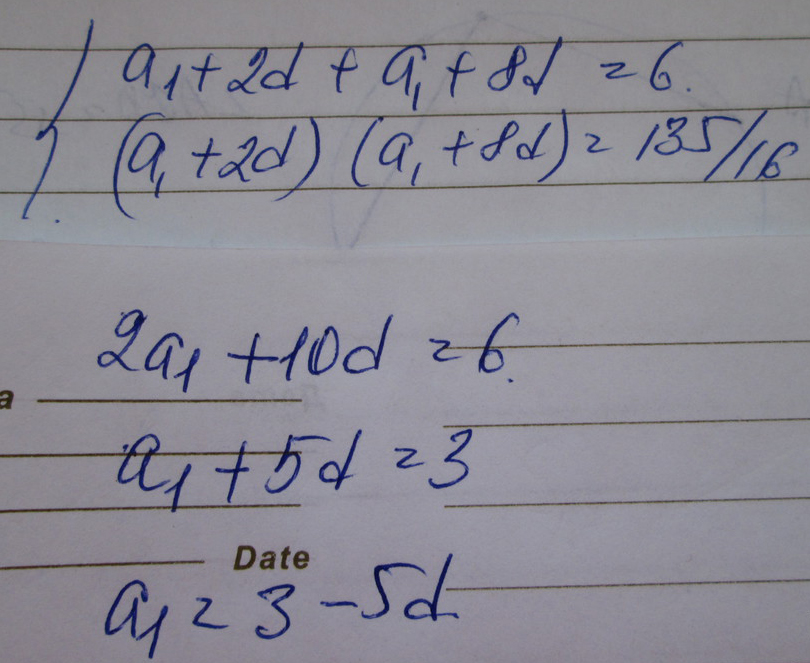прогрессия »
сумма первых членов арифметической прогрессии - страница 31
1Найдите двенадцатый член арифметической прогрессии 26;23;20. Вычислите сумму первых двенадцати ее членов.
2третий член арифметической прогрессии на 12 меньше шестого. Сумма восьмого и второго члена равна 4. Найдите второй и третий члены этой прогрессии
Решение: 1)a1 = 26
a2 = 23
a3 = 20
Для начала найдём разность арифметической прогрессии(d) : a2 - a1
23 - 26 = -3
Теперь мы можем найти a12 по формуле n-ого члена: an = a1 + (n-1)d
a12= 26 + 11 * (-3)
a12 = 26 + (33)
a12 = -7
Ну и теперь найдём сумму 12-ти членов прогрессии по формуле : Sn = (a1+an /2) * n
S12 = (26 + (-7) / 2)) * 12 = 114 2) Решение.1. a1=11; d=4; an=99; n=(an-a1)/d+1; n=(99-11)/4+1=23; Sn=0,5*(22+4*22)*23=1265.
2.d=12/3=4; 2*a1+8*d=4; a1=-14; a2=-10; a3=-6.1) Решите уравнение 2sin^2x=sin2x, если x принадлежит (-0.5pi;1.5pi)
2) Решите уравнение с модулем: /5-x/+/x-3/=2
3) Сумма третьего и девятого членов арифметической прогрессии равна 6, а их произведение равно 135/16. Найдите сумму 15 первых членов этой прогрессии
Решение: 5-х+3-х=2
-2х=-6
х=3
-(5-х) - (3-х) =2
-5+х-3+х=2
2х=10
х=5
2 sin^2x = 2 sinx cos x
sin^2x - sinx cos x =0 разделим уравнение на синус в квадрате
1 - ctgx =0
ctgx = 1
x =П/4 + Пn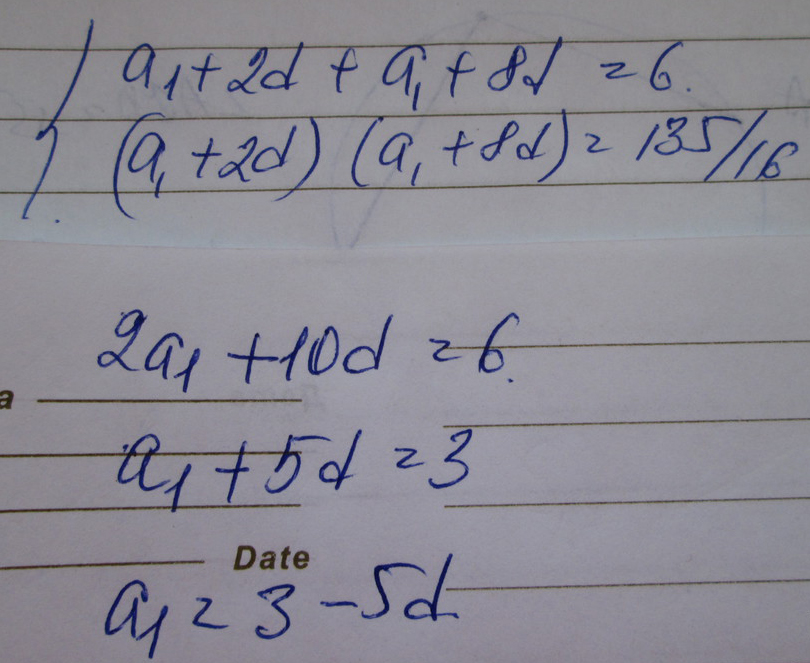
1) в арифметической прогрессии известны а4=1, а9=11. Найдите S20.
2) Найдите сумму двузначных чисел от 31 да 89.
3) Сумма первых двадцать пяти членов арифметической прогрессии равна 100. Найдите первый член этой прогресси, если а25= -44
Решение: 1). а4=1, а9=11. Найдите S20.Найдем разность прогрессии: d=(а9-а4)/(9-4)=(11-1)/5 = 10/5=2
a3=1-2=-1
a2=-1-2=-3
a1=-3-2=-5
a20=a1+19*(d)= -5+38=33
Sn = (a1+an)*n / 2
S20=(-5+33)*20/2=280
2). Получили арифм. последовательность: 31, 32, 33,89
a1=31 an=a(89-31)=a59=89 d=1
S59=(a1+an)*n / 2 = (31+89)*59/2 =3540
3). S25=100 a25=-44 a1-
Sn = (a1+an)*n / 2
S25 = (a1-44)*25/2 = 100
(a1-44)=8
a1=8+44
a1=52
Сумма первого и пятого членов возрастающей арифметической прогрессии равна 14,a произведение второго и четвертого ее членов равно 45. Найдите шестой член этой прогрессии
Решение: $$ \left \{ {{a_1+a_5=14} \atop {a_2*a_4=45}} \right. \\ \left \{ {{a_1+a_1+4d=14} \atop {(a_1+d)*(a_1+3d)=45}} \right. \\ \left \{ {{2a_1+4d=14} \atop {(a_1+d)*(a_1+3d)=45}} \right. \\ \left \{ {{a_1+2d=7} \atop {(a_1+d)*(a_1+3d)=45}} \right. \\ \left \{ {{a_1=7-2d} \atop {(7-2d+d)*(7-2d+3d)=45}} \right. \\ \left \{ {{a_1=7-2d} \atop {(7-d)*(7+d)=45}} \right. \\ \left \{ {{a_1=7-2d} \atop {49-d^2=45}} \right. \\ \left \{ {{a_1=7-2d} \atop {d^2=4}} \right. \\ d= \pm 2 $$
так как арифметическая прогрессия является возрастающей, значит $$ d=2 \\ \left \{ {{a_1=7-2d} \atop {d=2}} \right. \\ \left \{ {{a_1=3} \atop {d=2}} \right. \\ a_6=a_1+5d \\ a_6=3+5*2=13 $$
Ответ: $$ 13 $$Сумма первого третьего и пятого членов арифметической прогрессии равна -12, а произведение = 80. найти эту прогрессию.
Решение: Пусть первый член а
Третий а+2в
Пятый а+4а
Тогда сумма равна
а+а+2в+а+4в=3а+6в=-12
делим на 3
А+2в=-4
а=-4-2в
А произведение равно
а*(а+2в)*(а+4в)=80
(-4-2в)(-4-2в+2в)(-4-2в+4в)=80
-2(2-в)*(-4)*(-2)(2-в)=80
-16*(4-в^2)=80
4-в^2=-5
В^2=9
В1=-3
В2=3
Отсюда получаем при в=-3
а1=-4-2в=-4+6=2
а3=а1+2в=2-6=-4
а5=а1+4в=2-12=-10
При в=3
а1=-4-2в=-4-6=-10
а3=а1+2в=-10+6=-4
а5=а1+4в=-10+12=2