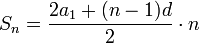прогрессия »

сумма первых членов арифметической прогрессии - страница 46

  • арифметическая прогрессия начинается так:-3,2,7. Найдите сумму первых пятидесяти ее членов


    Решение: n=50
    Найдем шаг прогрессии(d):
    7-2=5 
    Используя формулу(во вложении) 
    (2*(-3)+(50-1)*5)/2 * 50
     (-6+245)/2 * 50= 119.5 * 50 = 5975
    ответ: 5975 

    S=(2*(-3)+5*49)*50/2=5975

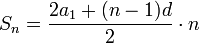
    n Найдем шаг прогрессии d -  Используя формулу во вложении   - -   -   . ответ  S -...

  • Арифметическая прогрессия представлена числами 11,13,15. Найдите сумму её первых шести членов.


    Решение: Сумму её первый шести членов можно найти по формуле

    Sn = n(a1+an)/2, а для 6 первых членов:

     S6 = 6(11+a6)/2 = 3(11+a6)

    Теперь найдем шестой член данной прогрессии по формуле:

    an = a1 + (n-1)*d

    d = a2 - a1 = 13 - 11 = 2

    a6 = 11 + 5*2 = 21

      S6 = 3(11+21) = 3*32 = 96 - сумма первых шести членов данной арифметической прогрессии

    $$ a_1=11 $$

    $$ d=13-11=2 $$

    $$ S_n=\frac{2a_1+(n-1)d}{2}*n $$

    $$ S_6=\frac{2*11+(6-1)*2}{2}*6=(22+5*2)*3=32*3=96 $$

  • Дана арифметическая прогрессия -6,2.2. Найдите сумму первых пятидесяти ее членов?


    Решение: d=4 это разность прогрессии
    формула суммы членов арифметической прогрессии
    S(n)=(a1+a(n))*n/2 то есть сумма первого и n члена умножается на количество членов и делится пополам
    a(n)=a1+(n-1)d 

    S=(-6+190)*50/2=4600

  • Дана арифметическая прогрессии:-4,2, 0. Найдите сумму первых десяти ее членов.
    Напишите формулу, которой вы пользовались, для нахождения.


    Решение: Можно решить 2 способами :
    1 способ
    1 число (-4)
    2 число (-2)
    3 число (0)
    4 число (2)
    5 число (4)
    6 число (6)
    7 число (8)
    8 число (10)
    9 число (12)
    10 число (14)
    и теперь просто складываете их
    6+8+10+12+14=50
    2 способ
    находим (d) : а-первого вычесть а-второе
    d = -4 -2 = 2
    далее надо по формуле
      2а-первого + d * ( n - 1)
    S=- * n.
      2
      2 * (-4) + 2 * (10 - 1)
    S=- * 10
      2
      -8 + 18
    S=- * 10
      2
    S= 10 * 5 = 50

  • 1) найти сумму первых восьми её членов если a1=2 a2=5

    2) найти сумму первых одинадцати её членов если a1=12, a2=10

    3) дана арифметическая прогресия 3;8;13. Найдите сумму первых семи ее членов.

    4) найти сумму первых пятнадцати её членов если a3=9, а4=5.


    Решение: a1=3; a2=7; a3=11;.
    d=4
    по формуле суммы первых n-членов арифмюпрогрессии
    S=((2*a1+(n-1)*d)/2)*n=((2*3+(5-1)*4)/2)*5=55
    n=5, т. к. надо найти сумму первых пяти членов

    1) d=3, a8=a1+7d, a8=2+21=23, S=(8(2+23))/2=100

    2) d=-2, a11=a1+10d=12-20=-8, S=(11(12-8))/2=22

    3) d=5, a7=a1+6d=3+30=33, S=(7(3+33))/2=126

    4) d=-4, a1=17, a15=a1+14d=17-56=-39, S=(15(17-39))/2=-165

<< < 444546 47 48 > >>