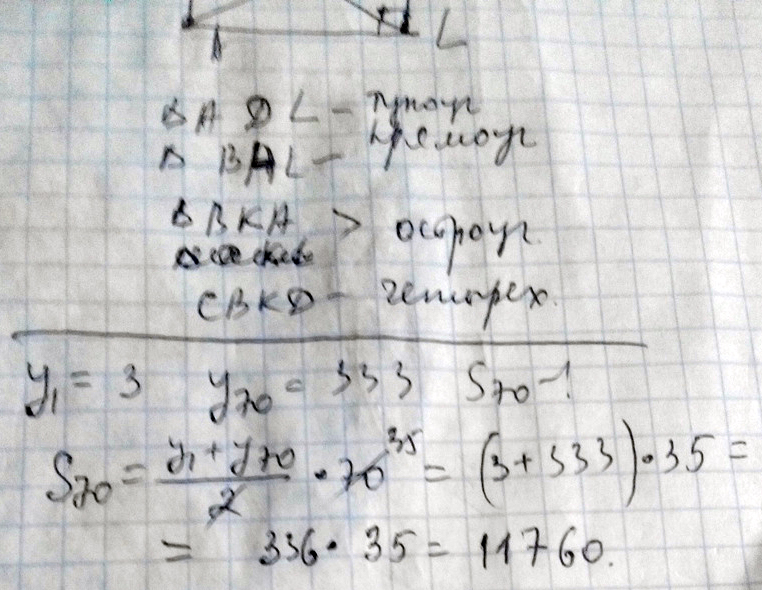прогрессия »

сумма первых членов арифметической прогрессии - страница 48

  • В арифметической прогрессии -7; -3; 1;. нийти сумму первых 12 членов.


    Решение: Данная задача может быть решена 2-мя способами:
    1) Найдем 12 член прогрессии:
    d=1-(-3)=4
    a1=-7
    a12=a1+d(n-1)=-7+4*11=44-7=37
    Найдем сумму 12 членов прогрессии:
    S=((a1+a12)*n)/2=((37-7)*12)/2=360/2=180
    Ответ: 180
    2) Найдем сумму 12 членов прогрессии сразу по формуле:
    S=((2a1+d(n-1))*n)/2=((2*(-7)+4*11)*12)/2=360/2=180
    Ответ: 180

  • В арифметической прогрессии y1=3,y70=333. найдите сумму 70 первых членов


    Решение: РЕШЕНИЕ
    Суммируем первое и последнее число и умножаем на половину таких пар.
    S = (y1+y70)*(1+70)/2 = 336*35 = 11760 - ОТВЕТ

    Формула суммы прогрессии

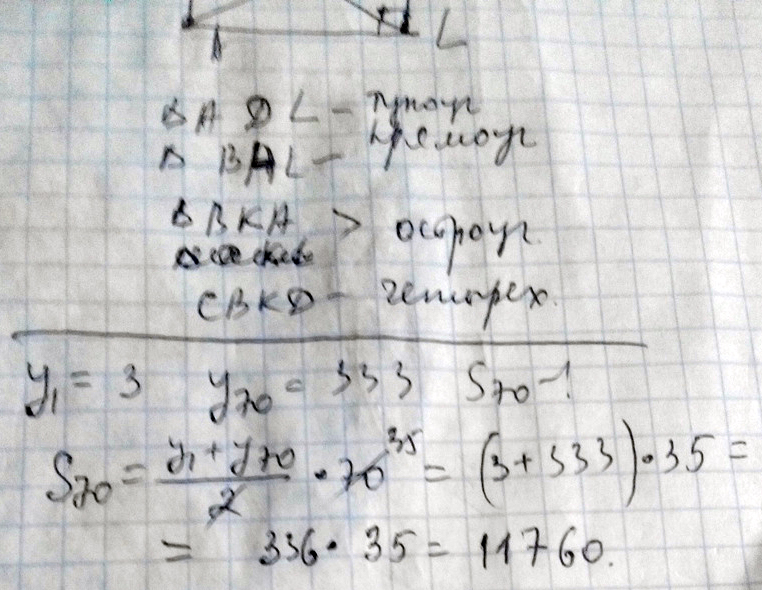
    РЕШЕНИЕСуммируем первое и последнее число и умножаем на половину таких пар.S y y - ОТВЕТ Формула суммы прогрессии...

  • В арифметической прогрессии: А2=(-7); А4=3. Найдите сумму первых шести членов прогрессии.


    Решение: A₂=-7 a₄=3
    Представим а₂ и а₄ как а₁ и а₃
    a₁ = -7
    a₃ = 3
     Имеем две формулы суммы членов ариф. пр.
    $$ Sn= \frac{a1+an}{2} *n $$
    $$ Sn = \frac{2a1+(n-1)d}{2}*n $$
    Узнаем сумму первых трех членов и выражаем d через 2-ю формулу:
    $$ Sn= \frac{-7+3}{2}*3=-6 $$
    $$ \frac{-14+2d}{2}*3 = -6 $$
    $$ d=5 $$
    a1= -12
    a6= -12+25=13
     
    $$ S _{6}= \frac{-12+13}{2}*6=3 $$

  • сумма первых четырех членов арифметической прогрессии в пять раз меньше суммы следующих восьми. найти отношение сумму первых восьми к сумме первых ее четрырех


    Решение: (a1+a2+a3+a4)*5 = a5+a6+.+a12

    an=a1+d(n-1)

    a1+a2+a3+a4=a1+(a1+d)+(a1+2d)+(a1+3d)=4a1+6d

    a5+a6+.+a12=8a1+60d

    (4a1+6d)*5=8a1+60d

    20a1+30d=8a1+60d

    12a1=30d|:6

    2a1=5d

    a1=2,5d

    a1+a2+.+a8            8a1+28d         8*2,5d +28d         20d+28d      48d

    _______________ = __________ = ______________= _________ =____ = 3

    a1+a2+.+a4               4a1+6d        4*2,5d+6d            10d+6d        16d

  • Сумма первых 100 членов арифметической прогрессии на 700 меньше, чем сумма следующих 100 ее членов. На сколько сумма первых трехсот членов этой прогрессии меньше суммы следующих трехсот ее членов


    Решение: A101 = a1 + 100d
    a102 = a2 + 100d
    a103 = a3 + 100d
    .
    a200 = a100 + 100d
    Складываем почленно все равенства, получаем, что сумма членов с 101 по 200 на 100*100d=10000d больше суммы первых 100 членов.
    Аналогично можно написать:
    a301 = a1 + 300d
    a302 = a2 + 300d
    .
    a600 = a300 + 300d
    Сумма первых 300 членов меньше суммы следующих 300 членов на 300*300d=9*10000d=9*700=6300

<< < 464748 49 50 > >>