прогрессия »

сумма первых членов арифметической прогрессии - страница 47

  • Арифметическая прогрессия начинается так: -3;2;7. Найдите сумму первых пятидесяти её членов.


    Решение: Прогрессия: -3;2;7.

    Из прогрессии видно, что разность арифм. прогрессии равна 5!

    а теперь записываем формулу суммы:

    S(50) =( 2a1+d*(n-1))*n/2

    Где:

    а1 = -3

    d=5

    n=50

    S(50)=(2*(-3) + 5*(50-1))*50/2

    S(50) = 5975

    Ответ:  5975

    -3,2,7,12,17,22,27,32,37, 42,47,52,57,62,67,72,77,82,87, 92,97,102,107,112,117,122,127,132, 137,142,147,152,157,162,167,172,177,182, 187,192,197,202,207,212,217, 222,227,232,237,242. Сумма этих первых пятидесяти членов=5975. и это будет ответом.

    a1 = -3

    a2 = 2

    d = a2-a1 = 2-(-3) = 5

    S n (эс энное) = 2 a1+ (n-1)d 2*(-3) + 49*5 -6+245

      __________ *n = __________ * 50 = _______ * 50 = 5975

      2 2 2

    n - номер нужного члена арифм. прогрессии, в данном случае пятидесятого

    a(n)=a(1)+d(n-1)=-3+5(50-1)=242
    S=((a(1)+a(n))/2)* n=(-3+242)/2*50=5975

  • 1.

    Найдите значение выражения 33*1/8-64*(1/8)³

    2.

    Дана арифметическя прогрессия -3/8;1/8;5/8;9/8. найдите сумму первых шеснадцати ее членов.

    3.

    решите систему неравенств

    в скобочках:

    18-4х≤0

    2х-14≤4

    4.

    В равнобедренном треуголнике FEK c основанием FK угол FEK равен 54⁰. Найдите величину внешнего угла при вершине K. Ответ дайте в градусах.


    Решение: Решаю последнее задание с треугольником:

    Так как в равнобедренном треугольнике углы при основании равны, а угол FEK = 54, то сумма углов F и K = 180-54 = 126. 126/2=63 градуса. Так же, мы знаем, чтобы найти внешний угол нужно найти сумму не смежных с ним углов. Итак. Внешний угол = 54+63=117 градусов

    Ответ: 177 градусов

  • Выписаны первые несколько членов арифметической прогрессии -3,1,5.
    Найдите сумму первых 60ти членов.)))


    Решение: Формула и обчисление

    A1=-3, a2=1, a=5, s60=?
    d=a2-a1=a3-a2=.
    d=1-(-3)=1+3=4
    d=4
    a60=a1+59.d, a60=-3+59.4=-3+236=233
    a60=233
    s60=60/2(a1+a60), s60=30.(-3+233)=30.230=6900
    s60=6900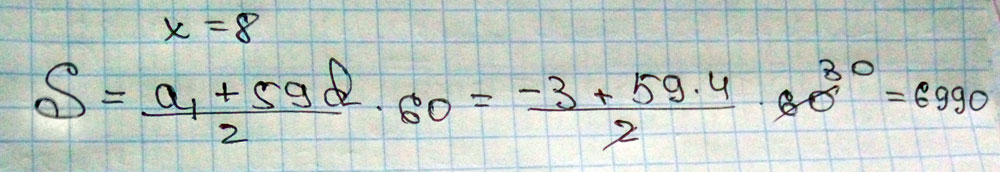

    Формула и обчисление A - a a s d a -a a -a .d - - d a a .d a - . - a s a a s . - . s...

  • Выписаны первые несколько членов арифметической прогрессии: 17; 32; 47;.
    Найдите сумму первых тринадцати её членов.


    Решение: Во первых, выведем формулу арифметической прогрессии:
    $$ a_n=a_1+d(n-1) $$ - формула любой арифметической прогрессии. $$ a_1 $$- первый член прогрессии. d - разность прогрессии.
    $$ d=32-17=15 $$ - разность прогрессии.
    $$ a_n=17+15(n-1) $$ - формула данной арифметической прогрессии.
    Во вторых, найдем 13-ый член данной прогрессии:
    $$ a_{13}=17+15(13-1)=17+15\cdot 12=197 $$
    А теперь сумму первых 13 членов:
    $$ \displaystyle S_n= \frac{a_1+a_n}{2}\cdot n $$ - общая формула суммы первых n членов. 
    $$ \displaystyle S_{13}= \frac{17+197}{2}\cdot 13= 107\cdot 13=1391 $$ - сумма первых 13 членов данной прогрессии.

  • как найти сумму первых 10-ти членов арифметической прогрессии если 2-й член = 6, а 8-й =24?


    Решение: Ну что бы найти d надо из 24-6=18 и поделить на 6 и будет равно 3, те а1=3 а3=9. и сложи хотя можно и по формуле

    $$ a_{2}=6, a_{8}=24, S_{10}-\\\\a_{2}=a_{1}+d\\a_{8}=a_{1}+7d\\\\ \left \{ {{a_{1}+d=6} \atop {a_{1}+7d=24}} \right.\\\\ \left \{ {{a_{1}=6-d} \atop {6-d+7d=24}} \right.\\\\ \left \{ {{a_{1}=6-d} \atop {6d=18|:6}} \right. \\\\ \left \{ {{a_{1}=6-d} \atop {d=3}} \right.\\\\\left \{ {{a_{1}=3} \atop {d=3}} \right. $$
    $$ a_{10}=a_{1}+9d=3+9*3=30\\\\S_{10}= \frac{a_{1}+a_{10}}{2}*10= \frac{3+30}{2}*10=33*5=165 $$

<< < 454647 48 49 > >>