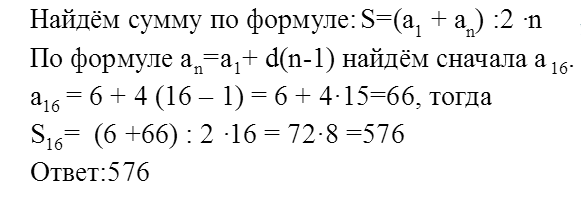прогрессия »

сумма первых членов арифметической прогрессии - страница 52

  • Найти сумму первых шестнадцати членов арифметической прогрессии, в которой 1) а1=6,d=4


    Решение: Здесь нужно рассчитывать по формуле: аn=a1+(n-1)*d 

    а2=6+(2-1)*4=10

    а3=6+(3-1)*4=14

    а4=6+(4-1)*4=18

    а5=6+(5-1)*4=22

    а6=6+(6-1)*4=26

    а7=6+(7-1)*4=30

    а8=6+(8-1)*4=34

    а9=6+(9-1)*4=38

    а10=6+(10-1)*4=42

    а11=6+(11-1)*4=46

    а12=6+(12-1)*4=50

    а13=6+(13-1)*4=54

    а14=6+(14-1)*4=58

    а15=6+(15-1)*4=62

    а16=6+(16-1)*4=66

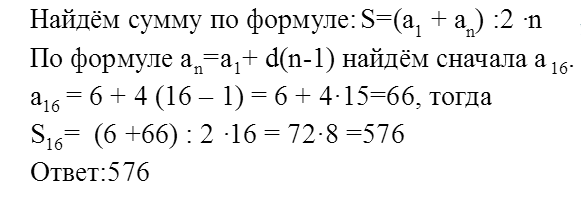
    Здесь нужно рассчитывать по формуле аn a n- d  а - а - а - а - а - а - а - а - а - а - а - а - а - а - а -...

  • найти сумму 22 первых членов арифметической прогрессии 25,30,35,40.


    Решение: (an) - арифметическая прогрессия

    а1=25, а2=30, следовательно d=a2-a1=5, 

    $$ S_{n} =\frac{2a{1}+d(n-1)}{2} * n $$

    из формулы суммы первых n членов арифметической прогрессии находим $$ S_{n}=\frac{50+5*21}{2}*22 = 1705 $$

    а1=25

    а2=30

    а3=35

    а4=40

    найти S(22)=?

    d=a(n+1)-a(n)=a2-a1=30-25

    d=5

    S(n)=((2*a1+d*(n-1))/2)*n

    S(22)=((2*25+5*21)/2)*22=((50+105)/2)*22=(155/2)*22=155*11

    S(22)=1705

  • Найти сумму первых девятнадцать членов арифметической прогрессии, если a4+a8+a12+a16=224


    Решение: Аn=a₁+(n-1)d *
    Согласно формуле * имеем 
    а₄+а₈+а₁₂+а₁₆=224
    а₁+3d+a₁+7d+a₁+11d+a₁+15d=224
    4a₁+36d=224
    a₁+9d=56
      согласно формуле суммы $$ s_{19}= \frac{a_{1}+a_{19}}{2}*19 \\ S_{19}= \frac{a_{1}+a_{1}+18d}{2}*19 \\ S_{19}= \frac{2a_{1}+18d}{2}*19 \\ S_{19}=(a_{1}+9d)*19=56*19=1064 \\ $$
    Ответ : сумма 19 членов ариф прогрессии равно 1064

    A4+a8+a12+a16=224
    a1+3d+a1+7d+a1+11d+a1+15d=224
    4a1+36d=224
    2(2a1+18d)=224
    2a1+18d=112
    S19=(2a1+18d)*19/2
    S19=112*19/2=56*19=1064 

  • Найти первые 50 членов двух арифметических прогрессий 2, 7, 12, и 3, 10, 17, которые одинаковы в обеих прогрессиях и найти их сумму S. В ответ записать S/100.


    Решение: Для первой прогрессии
    $$ a_1=2;a_=7;a_3=12 \\ d=a_2-a_1=7-2=5 \\ a_n=a_1+(n-1)*d=2+5(n-1)=2+5n-5=5n-3 $$
    для второй прогрессии
    $$ A_1=3;A_2=10;A_3=17 \\ D=A_2-A_1=10-3=7 \\ A_k=A_1+(k-1)*D=3+7(k-1)=7k-7+3=7k-4 \\ 5n-3=7k-4 \\ 7k-5n=1 $$
    нужно решить диофантовое уравнение от двух переменных в натуральных числах
    получим простым перебором находим "минимальное" решение в натуральных числах
    7*3-5*4=1
    $$ k_0=3;n_0=4 \\ k=3+5l \\ n=4+7l $$
    где \(l є N \cup {0}\)
    тогда формула искомых чисел
    $$ a_n=5*(4+7l)-3=20+35l-3=17+35l \\ A_n=7*(3+5l)-4=21+35l-4=17+35l $$
    где \(l є N \cup {0}\)
    первый член равен
    $$ L_1=17+35*0=17 $$
    50-й член равен
    $$ L_{50}=17+35*(50-1)=1732 $$
    Сумма первых 50-ти равна
    $$ S=\frac{L_1+L_{50}}{2}*50=\frac{17+1732}{2}*50=43725 \\ \frac{S}{100}=\frac{43725}{100}=437.25 $$
    -
    более просто можно было на первых членах проследить появление первого члена 17 и заметить что разность последовательности образованной с двух данных тоже является арифметической прогрессией с разностью равной 35

  • Найти первые 50 членов двух арифметических прогрессий 2;7;12;. и 3;10;17;. которые одинаковы в обеих прогрессиях и найти их сумму.


    Решение: Одинаковых чисел в этих арифм. прогрессиях не будет.
    Общий член ар. прогр.  $$ a_{n}=a_1+d(n-1) $$.
    Приравняем общие члены заданных ар. прогрессий:
    $$ 2+5(n-1)=3+7(n-1)\\\\2n=1\\\=\frac{1}{2} $$
    Получили, что номер члена ар. прогр. = 1/2, чего не может быть, т. к. номер - это натуральне число, n=1,2,3,4,5,6,

<< < 505152 53 54 > >>