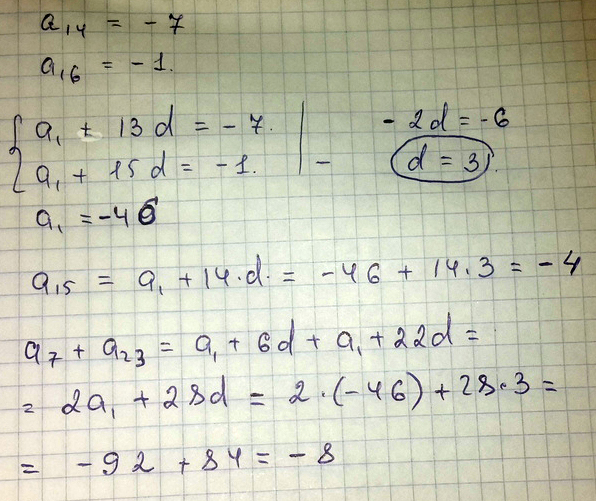прогрессия »

в арифметической прогрессии найдите - страница 3

  • В арифметической прогрессии (аn) а14 = -7, а16 = -1. Найдите а15 и а7 + а23


    Решение: ПРЕДСТАВИМ а14 как а1+13d, а а16 как а1+15d
    решаем как систему уравнений: -2d=-6 /(-2) d=3, отсюда находим а1= -7-39=-46
    отсюда находим а15=а1+14d=-46+14*3=-4
    a7+а23= а1+6d+а1+22d=2а1+28d= -8

    """""""""""""""""""""""""""""""""""""""""

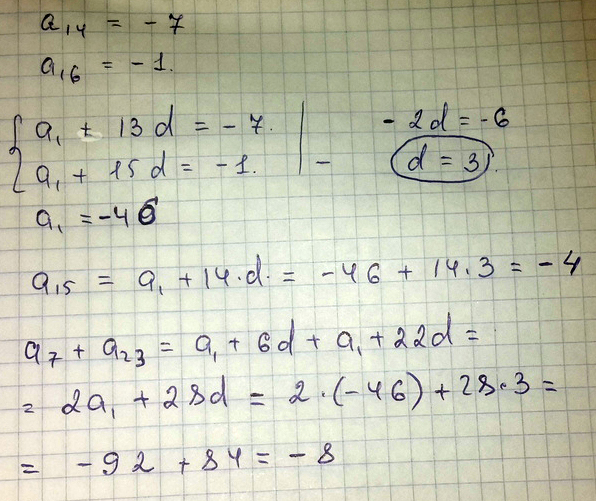
    ПРЕДСТАВИМ а как а d а а как а dрешаем как систему уравнений - d - - d отсюда находим а - - - отсюда находим а а d - - a а а d а d а d -...

  • в арифметической прогрессии a7=8 и a11=12,8. Найдите a1


    Решение: d=дробь числитель а11-а7 знаменатель 11-7=4,8/4=1.2

    d=1.2

    8=a1+1.2 * 6 

    8=а1+7.2

    a1=8-7.2=0.8

    a1=0.8

    an = a1 + (n-1)*d

    Получается система из двух уравнений:

    a7 = a1 + 6d = 8

    a11 = a1 + 10d = 12,8

    Из обоих выражаем а1:

    а1 = 8 - 6d

    a1 = 12,8 - 10d

    Приравниваем правые части:

    8 - 6d = 12,8 - 10d

    И решаем уравнение:

    4d = 12,8 - 8

    4d = 4,8

    d = 1,2.

    Теперь подставляем d в одно из выражений для нахождения а1:

    a1 = 8 - 6d = 8 - 6*1,2 = 8 - 7,2 = 0,8.

  • В арифметической прогрессии a7 = 8 и a11 = 12,8
    Найдите a1 и d.


    Решение: $$ a_7=8;a_{11}=12.8 $$
    $$ a_n=a_1+(n-1)*d $$
    $$ a_{11}-a_7=(a_1+(11-1)*d)-(a_1+(7-1)*d)=4d $$
    $$ 4d=12.8-8=4.8 $$
    $$ d=4.8:4=1.2 $$
    $$ a_1=a_n-(n-1)*d $$
    $$ a_1=8-(7-1)*1.2=8-6*1.2=8-7.2=0.8 $$

    $$ a _{7} =a _{1} +d(n-1) $$
    $$ a _{1} +6d=8 $$
    $$ a _{11} =a _{1} +d(n-1) $$
    $$ a _{1} +10d=12,8 $$
    $$ a _{1} +6d=8 $$
    -
    $$ a _{1} +10d=12,8 $$
    ______________________
    -4d=-4,8
    d=1,2; a1=0,8

  • В арифметической прогрессии(аn) a3=10 a7=40. Найдите a5


    Решение: Решение:
    Дано: а_3=10; а_7=40  Найти а_5
    Зная формулу: а_n=a1+d(n-1)
    Отсюда а_3=а1+d(n-1)=a1+d(3-1)=a1+2d
       a_7=a1+d(n-1)=a1+d(7-1)=a1+6d
    Или составим систему уравнений:
    10=a1+2d
    40=a1+6d
    Из первого уравнения найдём a1  a1=10-2d  и подставим во второе уравнение:
    40=10-2d+6d
    4d=30
    d=30/4=7,5
    a1=10-2*7,5=10-15=-5
    Зная а1 и d, можно найти:  а_5=-5+7,5(5-1)=-5+30=25
    Ответ: а5=25

  • В арифметической прогрессий a5=8,7 и a8=12,3. Найдите d и a1


    Решение: a5 = a1 + 4d = 8.7

    a8 = a1 + 7d = 12.3

    3d = 3.6

    d = 1.2

    a1 = 8.7 - 1.2*4 = 3.9 


    рассписываем по формуле 

    an =a1 + d (n - 1)

    a1

    a2=a1+1d

    a3=a1+d2

    a4=a1+3d

    a5=a1+4d

    a6=a1+5d

    a7=a1+6d

    a8 = a1 + 7d

    составим систему

    { a8=a1+7d

    {a5=a1+4d

    подставим числа и решим

    {12,3=a1+7d

    { 8,7=a1+4d

    {a1=12,3-7d

    {8,7=12,3-7d+4d

    8,7=12,3-3d

    3d=12,3-8,7

    d=1,2

    подставим d в уравнение a1=12,3-7d

    a1=12,3-6*1,2

    a1=3,9

<< < 123 4 5 > >>