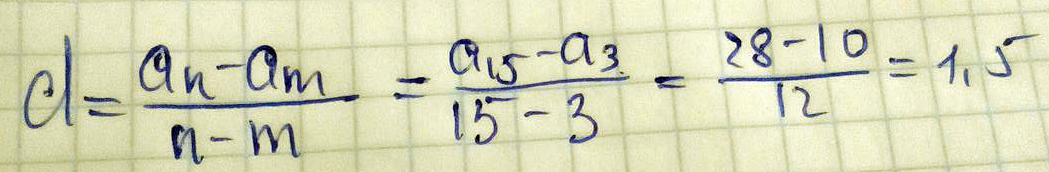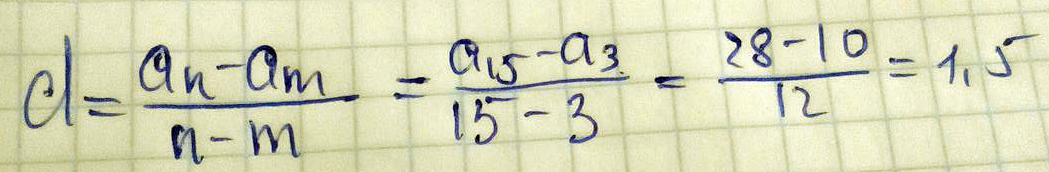прогрессия »
в арифметической прогрессии найдите - страница 5
в арифметической прогрессии найдите а3+а7, если а2+а4=7, а6+а8=23
Решение: 1) а1+а3+а5+а7+а9+а11 = а1+(а1+2d) +(а1+4d) +(а1+6d) +(а1+8d) +(а1+10d) = 6а1+30d =90
или а1+5d = 15
2) а2+а4+а6+а8+а10+а12 = (а1+d)+(а1+3d) +(а1+5d) +(а1+7d) +(а1+9d) +(а1+11d) = 6а1+36d = 78
или а1+6d = 13
3) решаем систему из двух уравнений
а) а1+5d = 15
б) а1+6d = 13 откуда
d = -2 и а1 = 25$$ a_n=\frac{a_{n-1}+a_{n+1}}{2} $$
$$ a_3=\frac{a_{2}+a_{4}}{2}=3,5 $$
$$ a_7=\frac{a_{6}+a_{8}}{2}=11,5 $$
$$ a_3+a_7=3,5+11,5=15 $$
В арифметической прогрессии (an) найдите n и an если a1= -12, d=1,5, Sn=13,5
Решение: Sn=2a1+d(n-1)*n/213.5=(-24+1.5(n-1))*n/2
13.5=(-24+1.5n-1.5)*n/2
13.5=(-24n+1.5n^2-1.5n)/2
-24n+1.5n^2-1.5n=27
1.5n^2-25.5n-27=0-умножаем на 2
3n^2-51n-54=0
n1=-1;n2=18
n=-1(не подходит, т. к n-натуральное число )
Следовательно, n=18
в арифметической прогрессии а5-а2=12, а2+а6=3Q, найдите S6?
Решение: a5=a1+4da2=a1+d
a6=a1+5d
a5-a2=12
a1+4d-a1+d=12
2a1+5d=12
a1=(12-5d)/2
a2+a6=30
a1+d+a1+5d=30
2a1+6d=30
a1+3d=15
a1=15-3d
следовательно
(12-5d)/2=15-3d
12-5d=30-6d
d=18
a1=15-3d
a1=15-54=-39
a6=a1+5d=-39+90=51
S6=(a1+a6)*n/2=(-39+51)*6/2=36
Ответ:36
В арифметической прогрессии известны S(20)=470 и S(80)=9080. Найдите S(100).
Решение: S₂₀=(a₁+a₂₀)*20=10(a₁+a₂₀)
2
S₈₀=(a₁+a₈₀)*80=40(a₁+a₈₀)
2
S₁₀₀=(a₁+a₁₀₀)*100=50(a₁+a₁₀₀)
2
10(a₁+a₂₀)=470
a₁+a₂₀=47
40(a₁+a₈₀)=9080
a₁+a₈₀=227
{a₁+a₁+19d=47
{a₁+a₁+79d=227
{2a₁+19d=47
{2a₁+79d=227
{2a₁=47-19d
{2a₁=227-79d
47-19d=227-79d
79d-19d=227-47
60d=180
d=3
2a₁=47-19*3
2a₁=47-57
2a₁=-10
a₁=-5
a₁₀₀=a₁+99d=-5+99*3=-5+297=292
S₁₀₀=50(-5+292)=50*287=14350
Ответ: S₁₀₀=14350В арифметической прогрессии a3=10,a15=28. Найдите разность прогрессии
Решение: А3=а1+2d
а15=а1+14d
(знак системы)10=а1+2d
(знак системы)28=а1+14d
-12d=-18
d=1,5
а1=7
S=2*7+1,5(15-1):2*15=16275
Ответ:16275