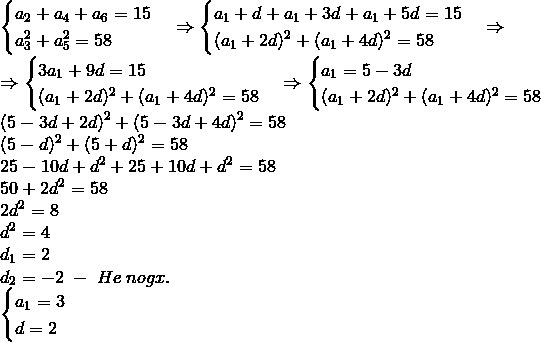член арифметической прогрессии равен - страница 3
если четвертый член равен 9, а девятый член равен-(-6), то сколько нужно взять членов арифметической прогрессии, чтобы сумма их равнялась 54?
Решение: $$ a_{4}=9, a_{9}=-6 $$$$ a_{4}=a_{1}+3d, a_{9}=a_{1}+8d $$
$$ \begin{cases} a_{1}+3d=9\\a_{1}+8d=-6 \end{cases} $$
Почленно складываем, получаем:
$$ 3d-8d=9-(-6) $$
$$ -5d=15 $$
$$ d=-3 $$
$$ a_{1}=9-3d=9-3(-3)=9+9=18 $$
Получаем прогрессию:
18, 15, 12, 9, 6, 3,
Видно, что в сумме первые четыре члена дают 54. (18+15+12+9=54)
Ответ: Надо взять первые четыре члена
$$ a_4=9; a_9=-6; a_n=a_{n-1}+(n-1)*d;a_4=a_1+3d;\\ a_9=a_1+8d;\\ a_9-a_4=(a_1+8d)-(a_1+3d)=5d; \\5d=(-6)-9=-15;\\ d=\frac {-15}{5}=-3;\\ a_1=a_4-3d;\\ a_1=9-3*(-3)=9+9=18;\\ S_n=\frac{2a_1+(n-1)*d}{2}*n;\\ S_n=54;\\ (2*18+(n-1)*(-3))n=54*2;\\ 36n-3n^2+3n-108=0;\\ n^2-13n+36=0;\\ (n-4)(n-9)=0;\\ n_1=4;\\ n_2=9 $$
ответ: 4 или 9 первых n членов
В арифметической прогрессии 10 членов, сумма членов с четными номерами равна 25, а сумма членов с нечетными равна 10. чему равен 7-ой член этой прогрессии?
Решение: $$ a_2=a_1+d\\a_4=a_1+3d\\a_6=a_1+5d\\a_8=a_1+7d\\a_{10}=a_1+9d\\\\a_2+a_4+a_6+a_8+a_{10}=5a_1+25d=25\\\\a_1+5d=5 $$
$$ a_1+a_3+a_5+a_7+a_9=\\=a_1+(a_1+2d)+(a_1+4d)+(a_1+6d)+(a_1+8d)=5a_1+20d=10\; \; \to \; \; \\\\a_1+4d=2\\\\ \left \{ {{a_1+5d=5} \atop {a_1+4d=2}} \right. $$
Вычтем из одного уравнения другое, получим
$$ d=3\;,\; \; a_1=5-5d=5-15=-10\\\\a_7=a_1+6d=-10+18=8 $$
Система
a1+a3+.+a9=10
a2+a4+.+a10=25
a1+a1+2d+.+a1+8d=10
a1+d+a1+3d+.+a1+9d=25
5a1+20d=10
5a1+25d=25
5d=15
d=3
a1=-10
a7=a1+6d=-10+18=8если второй и четвертый члены арифметической прогрессии соответственно равны 6 и 16, то пятый член прогрессии равен
Решение: n-й член арифметической прогрессии равен$$ a_n=a_1+d(n-1) $$составим состему уравнений для 2 и 4-го членов
$$ \begin{cases} a_1+d(2-1)=6\\a_1+d(4-1)=16 \end{cases}=>\\ \begin{cases} a_1+d=6\\a_1+3d=16 \end{cases}=>\\ \begin{cases} a_1=6-d\\6-d+3d=16 \end{cases}=>\\ \begin{cases} a_1=6-d\\2d=10 \end{cases}=>\\ \begin{cases} a_1=6-5\\d=5 \end{cases}=>\\ \begin{cases} a_1=1\\d=5 \end{cases}=>\\ $$
Сумма второго, четвертого и шестого членов возрастающей арифметической прогрессии равна 15, а сумма квадратов третьего и пятого членов этой же прогрессии равна 58.
Решение: Прогрессия возрастающая, значит, d>0.
$$ \begin{cases}a_2+a_4+a_6=15\\a_3^2+a_5^2=58\end{cases}\Rightarrow\begin{cases}a_1+d+a_1+3d+a_1+5d=15\\(a_1+2d)^2+(a_1+4d)^2=58\end{cases}\Rightarrow\\\Rightarrow\begin{cases}3a_1+9d=15\\(a_1+2d)^2+(a_1+4d)^2=58\end{cases}\Rightarrow\begin{cases}a_1=5-3d\\(a_1+2d)^2+(a_1+4d)^2=58\end{cases}\\(5-3d+2d)^2+(5-3d+4d)^2=58\\(5-d)^2+(5+d)^2=58\\25-10d+d^2+25+10d+d^2=58\\50+2d^2=58\\2d^2=8\\d^2=4\\d_1=2\\d_2=-2\;-\;He\;nogx.\\\begin{cases}a_1=3\\d=2\end{cases} $$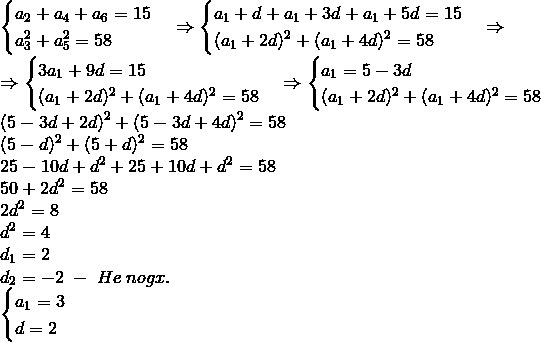
Восьмой член арифметической прогрессии составляет 40% от четвертого, а их сумма равна 2,8. Сколько нужно взять членов этой прогрессии, чтобы сумма их равнялась 14,3?
Решение: а₈ = 0,4а₄
а₈ + а₄ = 2,8
S(n)=14,3 ; n=?1. выражаем а₈ через а₄:
а₈ = 2,8 - а₄
2. приравниваем выражения и находим а₄:
0,4а₄ = 2,8 - а₄
1,4а₄ = 2,8
а₄ = 2
3. тогда а₈ = 2,8 - 2 = 0,8
4. составляем и решаем систему, выразив а₈ и а₄ через формулу арифметической прогрессии:
а₄ = а₁ + 3d
a₈ = a₁ + 7d
что в системе будет выглядеть как
а₁ + 3d = 2
a₁ + 7d = 0,8
решаем систему:
а₁ = 2 - 3d
2 - 3d + 7d = 0,8
4d = -1,2
d = -0,3
а₁ = 2,9
5. находим n по формуле суммы членов арифметической прогрессии:
14,3 = n(5,8 - 0,3(n-1)) / 2
n(5,8 - 0,3(n-1)) = 28,6
6,1n - 0,3n² = 28,6
0,3n² - 6,1n + 28,6 = 0 | x10
3n² - 61n + 286 = 0
D = 289
n = (61 ± 17) / 6 = 13; 10,1(6)
Так как целое n = 13, то 13 и будет нашим ответом.
Ответ: n = 13.