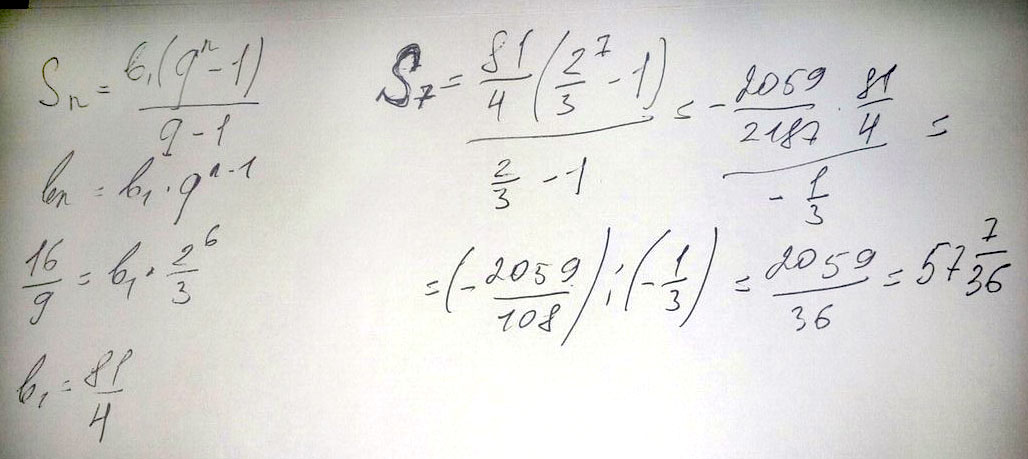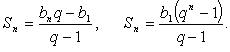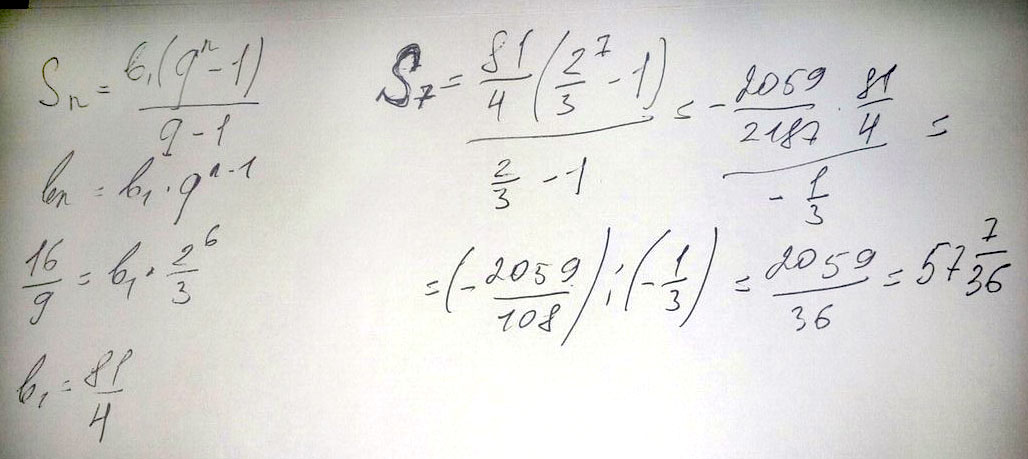прогрессия »
в геометрической прогрессии первый член равен - страница 10
Найдите сумму первых шести членов геометрической прогрессии 54;36;.;
Решение: Геометрическая прогрессия это последовательность чисел где каждое следующее получается из предыдущего умножением на постоянное число (q) называемое знаменателем.формула для вычисления n-го члена геометрической прогрессии:
a(n) = a1q^(n − 1)
q^(n − 1)=a(n)/а1
q=корень степени (n − 1) из [a(n)/а1]
q=корень степени (2 − 1) из [36/54] =корень степени (1) из [0,67] = 0,6667
тогда
1) Sn=a1*(q^6-1)/(q-1)
S6=54*(0,6667^6-1)/(0,6667-1)=148
2) a(n) = a1q^(n − 1)
а(3)=54*0,6667^(3 − 1)=24
а(4)=54*0,6667^(4 − 1)=16
а(5)=54*0,6667^(5 − 1)=11
а(6)=54*0,6667^(6 − 1)=7
Тогда
а1+а2+а3+а4+а5+а6=54+36+24+16+11+7=148
Ответ: сумма первых шести членов геометрической прогрессии равна 148
Найдите сумму первых 5 членов геометрической прогрессии:
1)b1=8, q=1/2 2)3; -6;. 3)-32;16;.4)c1=-4; q=3 5)u1=3; q=2
Решение: 1)
Sn=b₁*(1-qⁿ)/(1-q)
b₁=8 q=1/2 n=5
S₅=8*(1-(1/2)⁵)/ (1-1/2)=2³*(1-(1/2⁵)/(1/2)=(2³-2³/2⁵)*2=(2³-2⁻²)*2=
=2⁴-2⁻¹=32-1/2=31,5.
2)
a₁=3 a₂=-6.
q=-6/3=-2
S₅=3*(1-(-2)⁵)/(1-(-2))=3*(1+32)/3==33.
3)
-32; 16;. q=16/(-32)=-1/2
S₅=(-32*(1-(-1/2)⁵)/(1-(-1/2))=-32*(1+1/32)/(3/2)=-32*(1+1/32))*2/3=
=-4*33*2/(32*3)=-22.
4)
c₁=-4 q=3
S₅=4*(1-3⁵)/(1-3)=-4*(1-243)/(-2)=-4*(-242)/(-2)=-484.
5)u₁=3 q=2
S₅=3*(1-2⁵)/(1-2)=3*(1-32)/(-1)=3*(-31)/(-1)=93.
Найдите сумму первых десяти членов геометрической прогрессии х(n), если х2=-32 и q=-1/2
Решение: Найдём, х1= -32/-0.5=70Теперь по формуле суммы членой геометрической прогрессии:
70(0.5^10-1)/0.5-1=
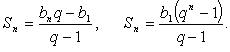
Найдите сумму первых 5 членов геометрической прогрессии: 3, -6, 12
Решение: 3(1-(-2)(5 степени):(делится на)1+2=3×33(поделить на 3)=33g= -2, так как -6/3= -2, и 12/ -6= -2. прогрессия выглядит так : 3,6, 12,24, 48. сумма равнв 3-6+12-24+48=33
Найдите сумму первых н членов геометрической прогрессии если в7 = 16/9 ; q =2/3 ; n=7
Решение: B7 = b1*q^6 => b1 = b7/q^6
b1 = 16/9 / (2/3)^6=16/9 * (3/2)^6=(2^4*3^6)/(3^2*2^6)=3^4/2^2=81/4
Sn=b1*(q^n-1)/(q-1)
S7=81/4 * ((2/3)^7-1) / (2/3 - 1) = 81/4 * (2^7/3^7 - 1) / (-1/3) = 3^4/2^2 * (2^7/3^7-1) * (-3) = -3^5/2^2 * 2^7/3^7 + 3^5/2^2 = 3^5/2^2 - (3^5*2^7)/(2^2*3^7)=243/4-32/9=(243*9-32*4)/(9*4)=2059/36.