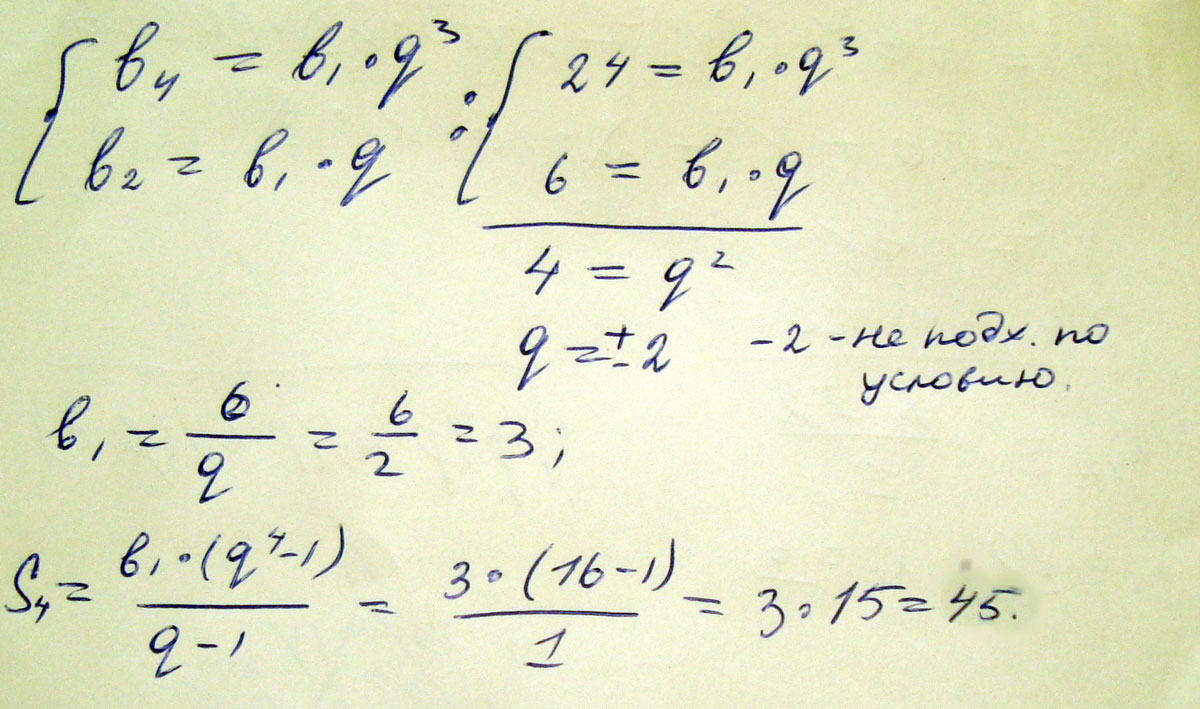прогрессия »

в геометрической прогрессии первый член равен - страница 15

  • Найдите сумму первых восьми членов геометрической прогрессии, если b2=6,b4=24


    Решение: Система решается методом деления.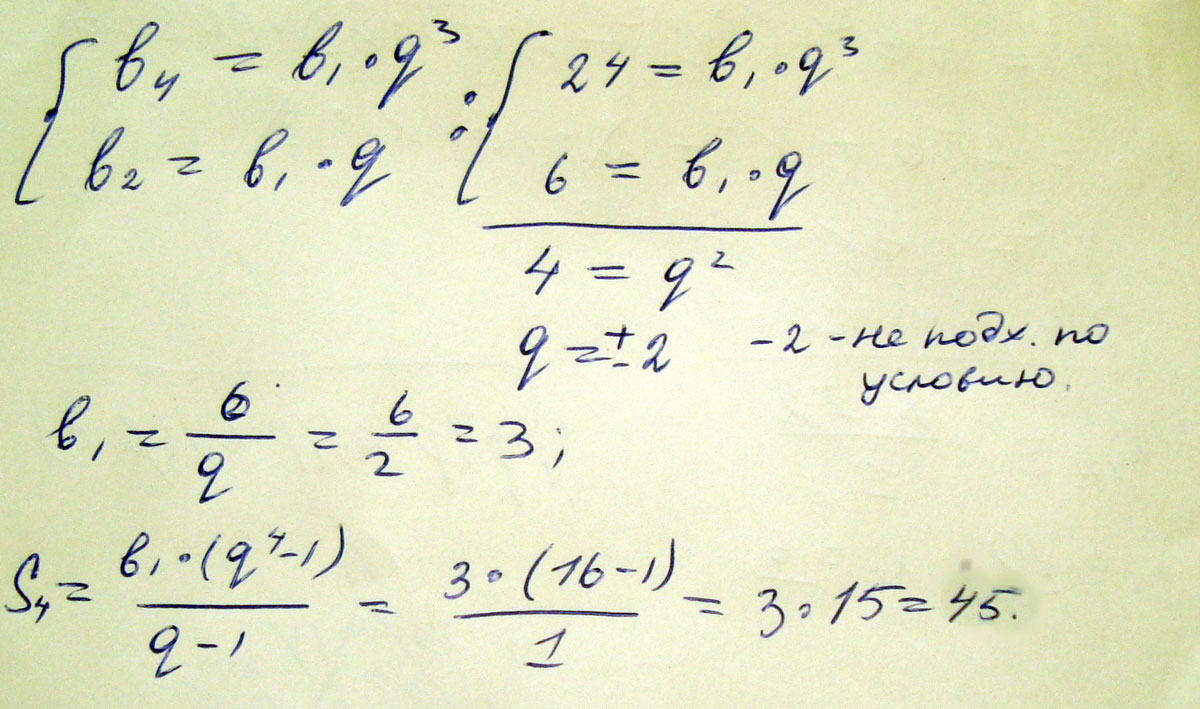 Система решается методом деления....

  • 1) Найдите сумму первых пяти членов геометрической прогрессии (bn), у которой b1=6, q=1/3
    2) Найдите сумму 2х+1+(1/2х)+.+(1/32х^5)


    Решение: 1)b1=6  q=1/3
    b5=b1*q^4
    b5=6*1/81=2/27
    S5=b1*(1-q^5)/(1-q)=6*(1-1/243):(1-1/3)=6*242/243*3/2=8 26/27
    2)b1=2x  b2=1  q=b2/b1=1/2x
    bn=1/32x^5
    1/32x^5=2x*1/(2x)^n-1
    1/(2x)^5=1/(2x)^n-2
    n-2=5
    n=7
    S7=b1*(1-q^7)/(1-q)
    S7=2x*(1-1/128x^7):(1-1/2x)=2x*(128x^7 -1)/128x^7 :(2x-1)/2x=
    =2x*(128x^7 -1)*2x/128x^7*(2x-1)=(128x^7-1)/32x^5*(2x-1)=
    =(2x-1)(64x^6+32x^5+16x^4+8x^3+4x²+2x+1)/32x^5*(2x-1)=
    =(64x^6+32x^5+16x^4+8x^3+4x²+2x+1)/32x^5

  • Найдите сумму первых шести членов геометрической прогрессии, если b1+b5=820, а знаменатель q=3


    Решение: $$ b_{1} + b_{1} *q^{4} =820 $$
    $$ b_{1} + b_{1} *3^{4} =820 $$
    $$ b_{1} + b_{1} *81 =820 $$
    $$ 82 b_{1} =820 $$
    $$ b_{1} =820:82 $$
    $$ b_{1} =10 $$
    $$ S_{6} = \frac{ b_{1} *(1- q^{6} )}{1-q} $$
    $$ S_{6} = \frac{10*(1- 3^{6} )}{1-3} = \frac{ 10 *(1- 729 )}{1-3} =3640 $$

  • Найдите сумму первых семи членов геометрической прогрессии(Bn), если:B7=72.9, q=1,5


    Решение: b7=q^6*b1

    S=(b1-bnq)/(1-q)=(bn/q^(n-1)-bnq))/(1-q)=

    =bn/(1-q)(q^(1-n)-q)=72.9*(1,5-(1,5)^(-6))*2=

    =145,8*(1,5-(1,5)^(-6))~145,8*1,41=205,9

    Вспоминаем формулу n-го члена геометрической прогресси :

    это Sn= bn*q- b1 \ q-1

    дальше ищем b1 

    b6= 72,9\1,5=48,6 b5=48,6\1,5=32,4 b4=32,4\1,5=21,6 b3= 21,6\1,5=14,4 b2=14,4\1,5=9,6

    b1=9,6\1,5=6,4

    подставляем все результаты в формулу

    S7=b7*1,5-b1\q-1

    S7=72,9*1,5-6,4\1,5-1=205,9

  • Найдите сумму шести первых членов геометрической прогрессии, если b2 = 0,08 b b4 = 1,28.


    Решение: b[2]=0.08

    b[4]=1.28

    b[n]=b[1]*q^(n-1)

    b[4]=b[2]*q^2

    q^2=b[4]/b[2]

    q^2=1.28/0.08=16

    q=4 или q=-4

    в первом случае

    b[1]=b[2]/q

    b[1]=0.08/4=0.02

    S[n]=b[1]*(q^n-1)/(q-1)

    S[6]=0.02*(4^6-1)/(4-1)=27.3

    во втором случае

    b[1]=b[2]/q

    b[1]=0.08/(-4)=-0.02

    S[n]=b[1]*(q^n-1)/(q-1)

    S[6]=-0.02*((-4)^6-1)/((-4)-1)=16.38

    ответ: 27.3 или 16.38

<< < 131415 16 17 > >>