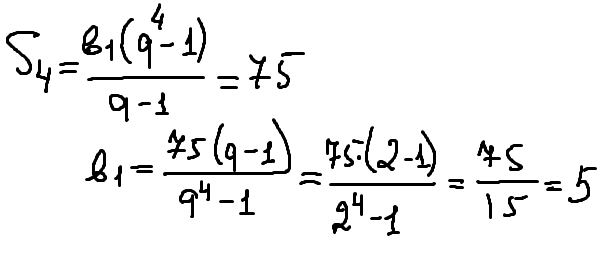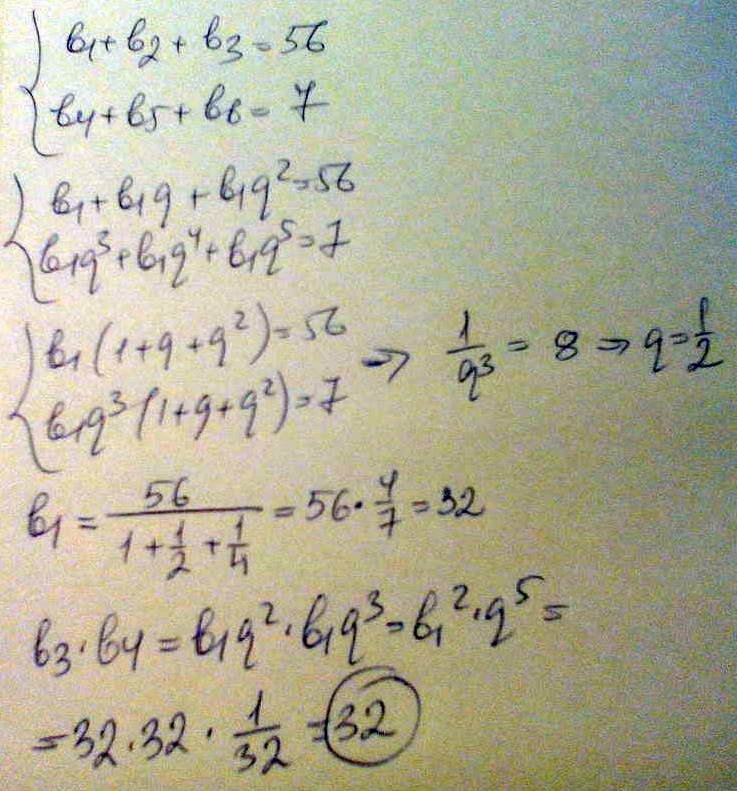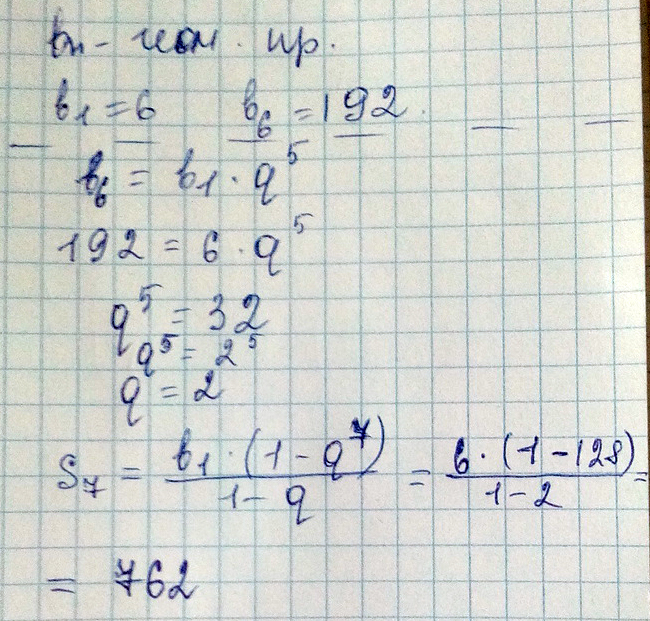прогрессия »

в геометрической прогрессии первый член равен - страница 35

  • Сумма всех членов геометрической прогрессии без первого члена равна 63.5, без последнего члена 127, без двух первых и без двух последних членов 30. Найти q и b1
    ( q вроде бы равно 0.5 )


    Решение: Воспользуемся формулой суммы
    $$ S= \frac{ b_{1} - b_{n}q }{1-q} $$
    сумма без первого члена будет следующая
    S=b(2)-b(n)q/1-q=b(1)q-b(n)q/1-q=q(b(1)-b(n))/1-q (b2=b1*q)=63.5  [1]
    сумма без последнего члена
    S=b(1)-b(n-1)q/1-q=b(1)-b(n)/1-q (b(n)=b(n-1)*q)=127  [2]
    из [1] и [2] получаем что q*127=63.5
    значит q=1/2
    составим последнее уравнение
    S=b(3)-b(n-2)*q/1-q=(b(1)*q²-b(n)*q/q²)/1-q=(b(1)*q²-b(n)/q)/1-q=30  [3]
    подставим q=1/2  в  [2] и [3], получим
    b(1)-b(n)/(1/2)=127  b(n)=b(1)-254
    b(1)/4-2b(n)/(1/2)=30 ⇒  b(1)/4-2(b(1)-254)=60  ⇒  b(1)-8(b(1)-254)=240
    ⇒-7b(1)=240-2032  ⇒  -7b(1)=-1792  b(1)=256
    Ответ  q=1/2,  b(1)=256

  • Сумма четырёх последовательных членов геометрической прогрессии со знаменателем 2 равна 75. Найдите первый член это прогрессии.


    Решение: S4=75

    q=2

    Sn=(b1(q^n -1))/(q-1) 

    75=(b1(16-1))/(2-1)

    75=15b1

    b1=5 

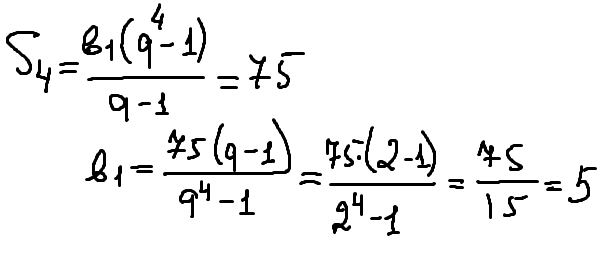
    S q Sn b q n - q-   b - - b b  ...

  • Cумма трех первых членов геометрической прогрессии равна 56, а сумма трех последующих ее членов равна 7. Найдите произведение третьего и четвертого членов этой прогрессии


    Решение: Сначала расписать каждый через. Первый член и знаменатель

    B1 + b2 + b3 = 56 b1 + b1q + b1q² = 56 b1 + b1q + b1q² = 56 
    b4 + b5 + b6 = 7 b1q^3 + b1q^4 + b1 q^5 = 7 q^3(b1 + b1q + b1q²) = 7
    Разделим первое уравнение на второе. Получим:
    1/q³ = 8 ⇒ q = 1/2 
    Подставим в первое уравнение найденный знаменатель
    b1 + b1·1/2 + b1·1/4 = 56
    7b1/4 = 56
    b1= 32
    Теперь ищем что спрашивают: b3·b4 = b1·q²·b1·q³ = ( b1)²·q^5 = 32²·(1/2)^5= 32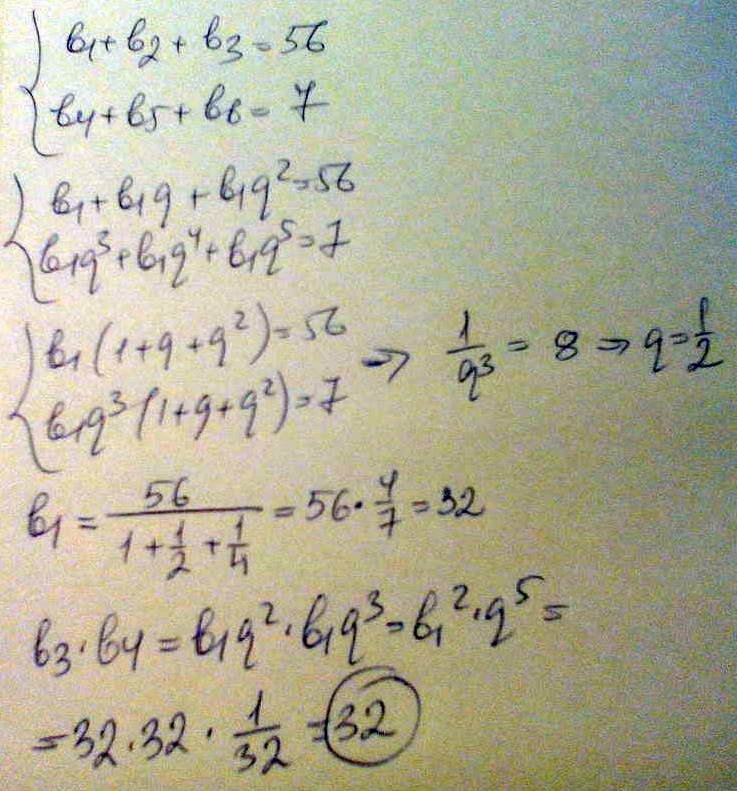

    Сначала расписать каждый через. Первый член и знаменатель B b b b b q b q b b q b q   b b b b q b q b q q b b q b q Разделим первое уравнение на второе. Получим q    q  Подст...

  • Чему равна сумма семи первых членов геометрической прогрессии (Bn), если b1 = 6, а b6 = 192.


    Решение: S(n)=(b1-bn*q)/1-q; b1=6, b6=192; b6=6*q^5; q^5=192/6; q^5=32 |=> q=2 b7=6*2^6=384 S(7)=6-384*2/1-2=-762/-1=762 Ответ: S(7)=762

    Сумма первых семи членов геометрической прогрессии равна 762

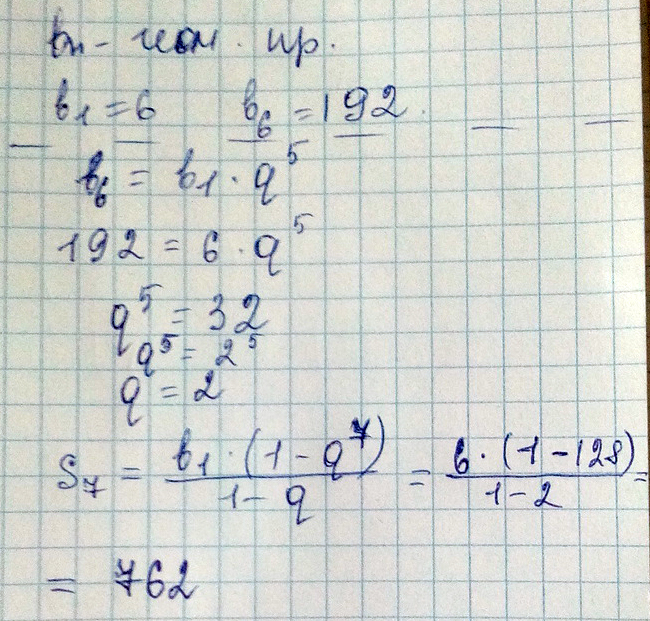
    S n b -bn q -q b b b q q q gt q b S - - - - Ответ S Сумма первых семи членов геометрической прогрессии равна...

  • В геометрической прогрессии пять членов, сумма их без первого члена равна 30, а без последнего члена равна 15. Найдите третий член прогрессии.


    Решение: $$ b_n=b_1\cdot q^{n-1};\\ b_1,\ b_2,\ b_3,\ b_4\ b_5;\\ S_{2.5}=30;\\ S_{1.4}=15;\\ S_{2.5}=S_5-b_1=b_1\frac{q^5-1}{q-1}-b_1=b_1\left(\frac{q^5-1-1+1}{q-1}\right)=\\ =b_1\frac{q^5-q}{q-1}=\frac{q(q^4-1)}{q-1}=b_1\cdot q\cdot\frac{(q-1)\cdot(q^3+q^2+q+1)}{q-1}=\\ b_1q(q^3+q^2+q+1)=30;\\ S_{1.4}=S_4=b_1\frac{q^4-1}{q-1}=b_1\frac{(q-1)(q^3+q^2+q+1)}{q-1}=\\ =b_1(q^3+q^2+q+1)=15;\\ $$
    $$ \left \{ {{S{2.5}=q\cdot S4=30} \atop {S_{1.4}=S_4=15}} \right. \left \{ {{b_1(q^3+q^2+q+1)=30} \atop {b_1(q^3+q^2+q+1)=15}} \right. \\ q=\frac{S_{2.5}}{S_{1.4}}=\frac{qS_4}{S_4}=\frac{30}{15}=2;\\ q=2;\\ S_4=b_1(q^3+q^2+q+1)=15;\\ b_1(2^3+2^2+2^1+1)=15;\\ b_1(8+4+2+1)=15;\\ b_1\cdot15=15;\\ b_1=\frac{15}{15}=1;\\ S_4=1\cdot{2^4-1}{2-1}=1\cdot\frac{16-1}{1}=1\cdot15=15;\\ S_{2.5}=S_5-b_1=1\cdot\frac{2^5-1}{2-1}-1=1\cdot\frac{32-1}{2-1}-1=1\cdot31-1=31-1=30;\\ $$
    $$ b_3=b_1\cdot q^{3-1}=b_1\cdot q^2=1\cdot2^2=1\cdot4=4;\\ b_3=4. $$

<< < 333435 36 37 > >>