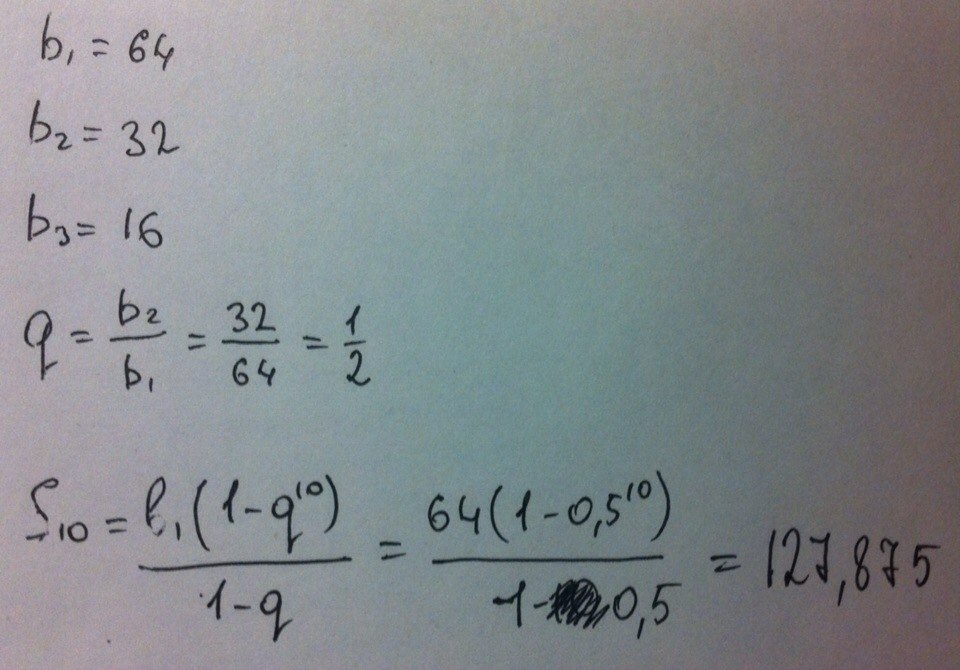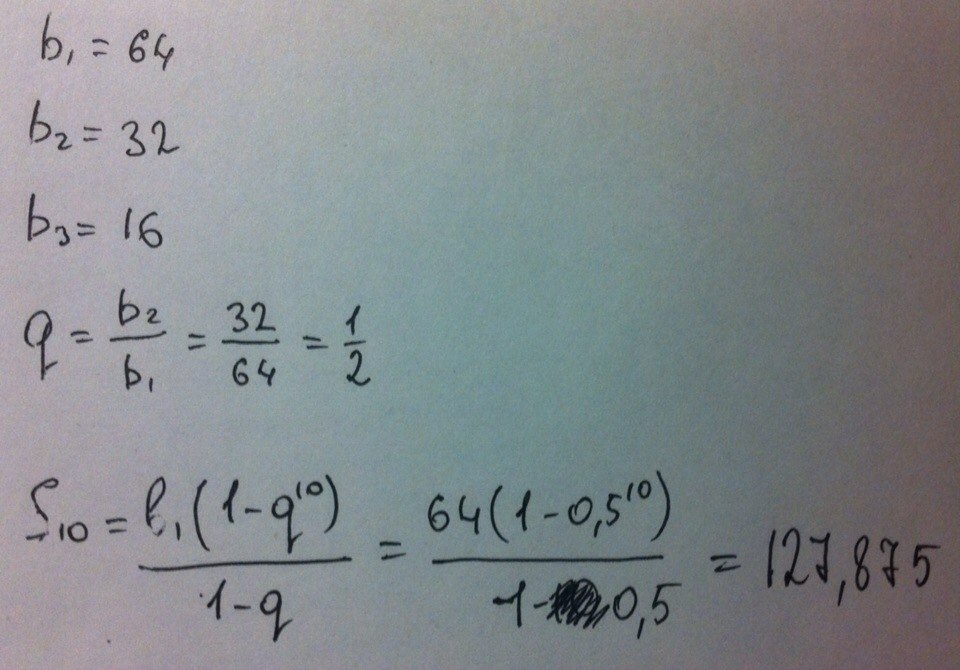прогрессия »
в геометрической прогрессии первый член равен - страница 38
В геометрической прогрессии сумма первого и пятого члена равна 51, а сумма 2 и 6 члена=102. Сколько членов этой прогрессии нужно взять, чтобы из сумма была 3069
Решение: Составляем уравнения
1. b1 + b5 = 51
b1 + b1*q^4 = 51
b1 * (1+q^4) = 51
2. b2 + b6 = 102
b1*q + b1*q^5 = 102
b1*q * (1+q^4) = 102
Второе уравнение разделим на первое. Получим
q = 2
Подставляем в первое уравнение и находим b1
b1 * (1+q^4) = 51
b1 * (1+2^4) = 51
b1 * 17 = 51
b1 = 3
Используем формулу суммы n членов
S = b1 * (q^n - 1) / (q - 1)
3 * (2^n - 1) / (2 - 1) = 3069
2^n - 1 = 1023
2^n = 1024
n = 10
Ответ: нужно взять 10 членов, включая первыйДана геометрическая прогрессия: 2;4;8;.
а) найдите шестой член прогрессии.
б) найдите сумму первых 6членов прогрессии
Решение: А) 2;4;8.(bn). b1=2, q=b2:b1=4:2=2. b5- bn=b1*(q в степени n-1). b5=2*(2) в степени 5-1. b5=2*(2) в 4 степени. b5=2*16=32. Ответ. Шестой член данной геометрической прогрессии равен 32. б)2;4;8;.(bn). b1=2, q=4:2=2. S6- Sn=в числителе b1*(q в степени n)-1): ( в знаменателе)q -1. S6=2*(1-(2) в 6 степени: 1-2. S6=2*(1-64):(-1). S6=2*(-63):(-1). S6=-2*(-63). S6=126. Ответ. Сумма 6 первых членов геометрической прогрессии равна 126.Дана геометрическая прогрессия 128,64, 32, найдите сумму ее первых шестой членов с нечетными номерами
Решение: Можно просто найти значение нечетных чисел этой прогрессии до 6
1 имеется, 3, имеется, найдем 5
Найти четвертый член и потом через него пятый
Но для начала нужно найти знаменатель.
b2/b1=-64/128=-0.5
b4=32*-0.5=-16
b5=-16*-0.5=8
b1+b3+b5 и будет суммой первых шести членов с нечетными номерами.
128+32+8=168
Cумма первых шести нечетных членов геометрической прогрессии равна 168.
Дана геометрическая прогрессия 2,6, 18? Найдите сумму ее первых пяти отрицательных членов.
Решение: Найдем знаменатель данной прогрессиии он равен -3, составим с учетом знаменателя последовательность отрицательных членов: -6,54,
Для данной последовательности знаменатель будет равен 9.
Вычислим сумму пяти членов по формуле
$$ S_{5} = \frac{-6*(1- 9^{5} }{1-9} = \frac{-6*(-59048)}{-8} =-44286 $$
Сумма пяти отрицательных членов равна -44286Дана геометрическая прогрессия 64;32;16. Найдите сумму первых десяти ее членов.
Решение: Находите, какая разность между числами 64 и 32 потом из этих чисел нашла разность и прибавляй и найдетеB₁ = 64
b₂ = 32
b₃ = 16
q = b₂/b₁
Sn = (b1*(1-q^n))/(1-q)
Ответ: S₁₀ = 127,875