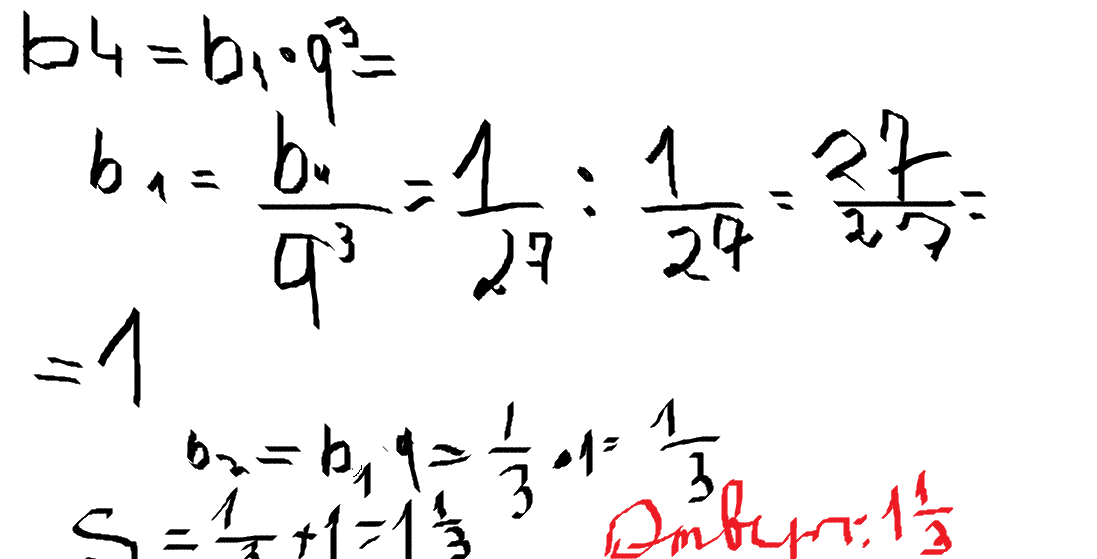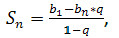в геометрической прогрессии первый член равен - страница 39
Дана геометрическая прогрессия(bn). Вычислите сумму 2 первых членов, если b4=1/27,q=1/3
Решение: $$ b_{4}= \frac{1}{27},q= \frac{1}{3}\\\\b_{2}=b_{4}:q^2= \frac{1}{27}:(\frac{1}{3})^2=\frac{1}{27}:\frac{1}{9}=\frac{1}{27}*\frac{9}{1}=\frac{1}{3}\\\\b_{1}=b_{2}:q=\frac{1}{3}:\frac{1}{3}=1\\\\S_{2}=b_{1}+b_{2}=1+\frac{1}{3}=1\frac{1}{3} $$Примерно вот так я решил. Можете отметить как лучшее
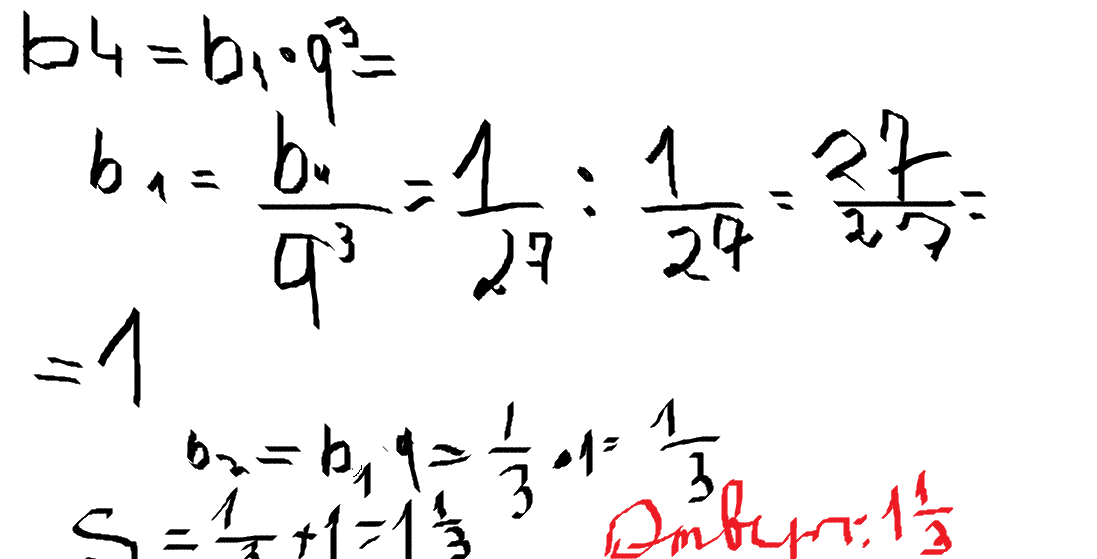
Дана геометрическая прогрессия: -9,3,1. Найдите произведение первых пяти ее членов.
Решение: Находим знаменатель геометрической прогрессии, то есть qДля этого делим 3 на -9 и получаем - 1/3 ( минус одна третья )
Хотелось бы уточнить на счет произведения первых пяти членов. Видимо там все таки имеется ввиду сумма. Если так то находим сумму:
S= 9((-1/3)^5 - 1) / -1/3 - 1 = - 0,27/-1,33 = 0,2 Вуа-ля =)
Если же все таки произведение то тебе следует найти 4 и 5 член прогрессии. Для этого просто умножай предыдущее число на знаменатель то есть на -1/3
Дана геометрическая прогрессия 2,6,18.
Найдите сумму первых пяти её членов
Решение: Формула ( там не х. а n стоит, но у меня нет надстрочной и подстррочной n для обозначенияn-ого члена прогрессии, поэтому поставила ᵡ):
Sᵪ = A1·(qᵡ - 1)/(q - 1)
S₅ = 2·(3⁵- 1):(3 - 1) =(3⁵- 1)= 242
Дана геометрическая прогрессия 4,2,1. Найдите сумму первых пяти ее членов
Решение: Найдем шаг прогресси:2:4 = 1\2.
Далее найдем оставшиеся два неизвестных члена прогрессии, умножая предыдущий на шаг:
4, 2, 1, 1*1\2 = 0.5, 0.5 * 1\2 = 0.25
Теперь найдем их сумму:
4+2+1+0,5+0,25=6.75
Ответ:6,75.
А вообще для таких дел есть формула
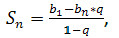
дана геометрическая прогрессия. Вычислите сумму 3 первых членов, если b4=-24, q=-2
Решение: b3 = -24:(-2) = 12b2 = 12:(-2) = -6
b1 = -6:(-2) = 3
$$ S = \frac{b1*(q^{3}-1)}{q-1} $$ = $$ \frac{3 * ((-2)^{3}-1)}{-2-1} = \frac{3*(-8-1)}{-3} = \frac{3*(-9)}{-3} = \frac{-27}{-3} = 9 $$
-24:(-2)=12 -b3
12:(-2)=-6-b2
-6:(-2)=3 -b1
S3= 3(-8-3)/-2-1=-33/-3=11
ответ:11
это правильней если там с минусами