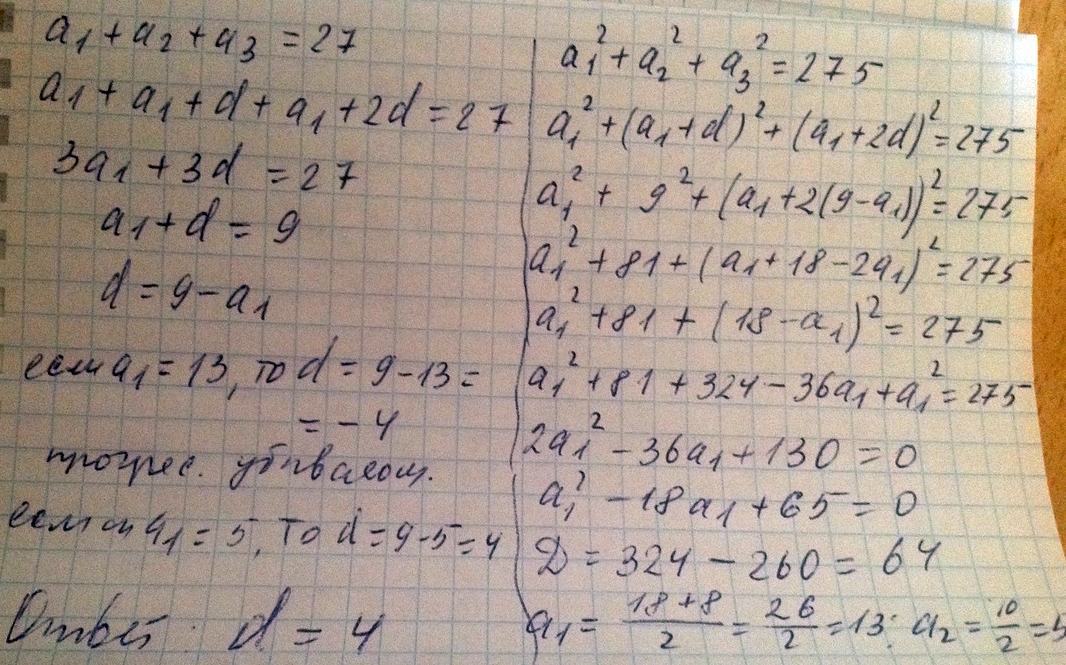прогрессия »

разность членов арифметической прогрессии - страница 11

  • Сумма первых шести членов арифметической прогрессии равна 9, разность между четвертым и вторым членами 0,4. Найдите первый член арифметической прогрессии


    Решение: Выражаем четвертый член прогрессии (а4) через второй (а2): а4-а2=0,4 откуда а4=а2+0,4 Свойство: Любой член арифметической прогрессии, начиная со второго, является средним арифметическим предыдущего и следующего члена прогрессии: Значит а3=(а2+а4)/2 или а3=(а2+а2+0,4)/2=а2+0,2 или а3-а2=0,2 Т. о. шаг арифметической прогресси равен 0,2. Сумма 6 первых членов арифметической прогрессии выражается формулой: S6=((2a1+d*5)/2)*6, где d=0,2 Подставляем значения: 9/6=а1+1/2 или 1,5=а1+0,5 откуда а1=1. Ответ: а1=1, прогрессия имеет вид: а1=1, а2=1,2, а3=1,4, а4=1,6, а5=1,8, а6=2 Проверка: Сумма: равна 9 разность а4-а2=1,6-1,2=0,4.

    A₄=a₁+d, a₂=a₁+d, a₄-a₂=a₁+3d-a₁-d, a₄-a₁=2d, 2d=0,4, d=0,2. S₆=(2a₁+5d)*6/2, 3(2a₁+5*0,2)=9, 2a₁+1=3, 2a₁=2, a₁=1. Ответ: a₁=1, d=0,2

  • В арифметической прогрессии сумма первых шесть членов равна 3, а сумма первых восьми членов прогрессии равна 12. Найдите разность прогрессии


    Решение: $$ S_{6} $$ = 6a1 + 15d = 3
    $$ S_{8} $$ = 8a1 + 28d = 12
    Умножаем 1 - ое уравнение на 4 и приравниваем ко 2 - му ->
    16a1 = 32d
    a1 = 2d
    Подставляем к 1-му уравнению a1 = 2d ->
    12d + 15d = 3
    27d = 3
    d = 1 / 9

    S₁ = (a₁+a₆)·6 / 2
    S₂ = (a₁+a₈)·8 /2
    3=(a₁+a₆)·3 a₁+a₆=1 (1)
    12=(a₁+a₈)·4 a₁+a₈=3 (2)
    a₆=a₁+d(6-1) a₆=a₁+5d (3)
    a₈=a₁+d(8-1) a₈=a₁+7d (4)
    подставим (3) в (1), а (4) во (2), получаем
    2а₁+5d=1 (5)
    2a₁+7d=3 (6) (5) - (6) 
    -2d = -2
    d = 1

  • Три числа, сумма которых равна 84, образуют геометрическую прогрессию. Они являются первым, шестым и шестнадцатым членами арифметической прогрессии, разность которой отлична от нуля. Найдите наибольшее из этих чисел.


    Решение: Знаменатель геометрической прогрессии должен быть равен 2, тогда, если х - первое число, то 2х - второе число, 4х - третье число, по условию сумма чисел 84, поэтому х+2х+4х = 84, 7х = 84, х = 12, 2х = 24, 4х = 48. Действительно, эта тройка чисел подходит и для арифметической прогрессии: 12 = 24-5d; 5d = 12; d = 2,4; 12 = 48-15d; 15d = 36; d = 2,4 ; 2,4 = 2,4 (верно). Наибольшее из трёх чисел = 48. Ответ: 48.

  • найдите разность возрастающей арифметической прогрессии, у которой сумма первых трех членов равна 27, а сумма их квадратов равна 275


    Решение: a1+a2+a3=27

    a1^2 + a2^2 + a3^2=275

    a3=a1+2d

    a2=a1+d

    a1+a1+d+a1+2d=27

    3(a1+d)=27

    a1+d=9

    a1=9-d

    (a1)^2 + (a1+d)^2 + (a1+2d)^2=275

    81 - 18d + d^2 + 81 + 81 + 18d + d^2=275

    243 + 2d^2=275

    2d^2=32

    d^2=16

    d=4

    Решение Вашего задания во вложении 

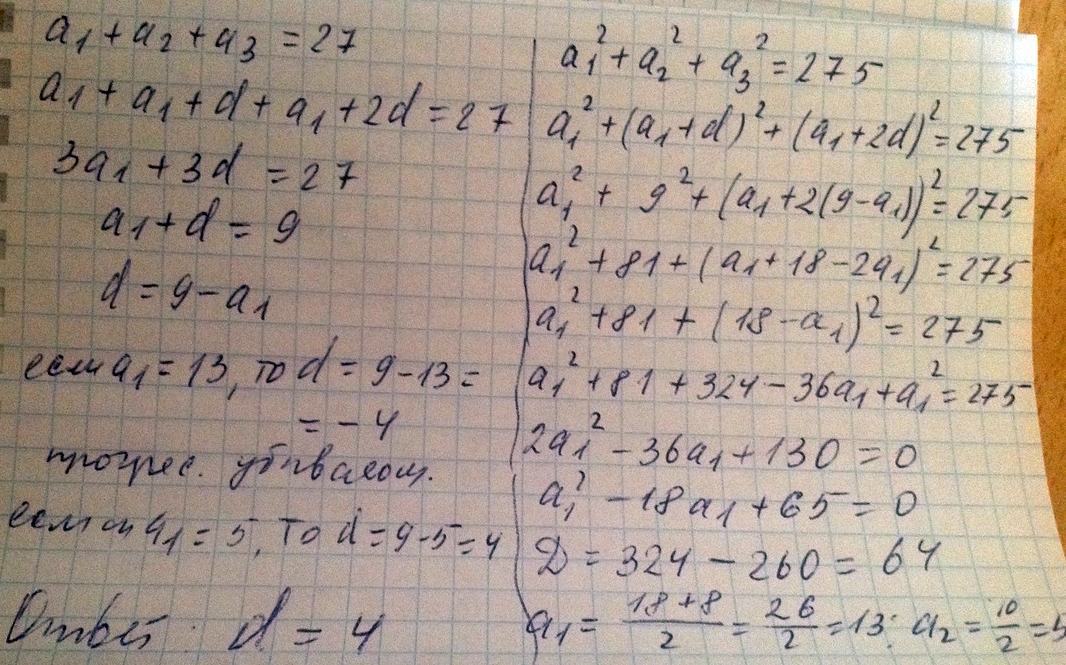
    a a a a a a a a d a a d a a d a d a d a d a -d a a d a d - d d d d d d d d Решение Вашего задания во вложении ...

  • Найдите первый член арифметической прогрессии, если её разность равна 8, а сумма первых 20 членов равна сумме следующих за ними десяти членов этой прогрессии.


    Решение: N-ый член арифметической прогрессии равен $$ a_{n}=a_{1}+d(n-1) $$
    Сумма с 1 по 20 члены арифметической прогрессии равна:
    $$ \frac{a_{1}+a_{20}}{2}*20= (a_{1}+a_{1}+d(20-1))*10=10(2a_{1}+19d) $$
    Сумма с 21 по 30 члены арифметической прогрессии равна:
    $$ \frac{a_{21}+a_{30}}{2}*10= (a_{1}+d(21-1)+a_{1}+d(30-1))*5=5(2a_{1}+49d) $$
    По условию, суммы равны.
    $$ 10(2a_{1}+19d)=5(2a_{1}+49d) \\ 2(2a_{1}+19d)=2a_{1}+49d \\ 4a_{1}+38d-2a_{1}-49d=0 \\ 2a_{1}=9d \\ a_{1}= \frac{9d}{2} \\ a_{1}= \frac{9*8}{2} =36 $$

<< < 91011 12 13 > >>