прогрессия »

разность членов арифметической прогрессии - страница 9

  • 1. Дана арифметическая прогрессия 16,9; 15,6;. Найдите 11-й член и разность прогрессии.
    2. Найдите 1-ый член арифметической прогрессии, если a3 = - 2,3; a8 = - 0,8


    Решение: 1. Дано: a1=16.9, a2=15.6
    Найти: a11
      Решение:
    Разность: d=a2-a1=15.6-16.9=-1.3
    Член прогрессии:
     
    a11=a1+10d=3.9
    Ответ: 3,9.
    2. Дано: a3=-2.3, a8=-0.8
    Найти: a1.
      Решение:
    Разность: d=(an-am)/(n-m)=(a8-a3)/(8-3)=(-0.2+2.3)/5=0.3
    Первый член прогрессии: 
    a1=an-(n-1)d=a3-2d=-2.9
    Ответ: -2,9

  • Дана арифметическая прогрессия (an), разность которой равна 5,3,a1=-2. Найдите сумму первых 9 ее членов


    Решение: Сумма первых 9 членов арифметической прогрессии равна
    2*(-2)+5,3*(9-1)/2 умножить на 9=172,8
    Формула:Sn=2а первых +d*(n-1) *n
      2
     где:a-первое это первый член арифм. прогрессии
      d-разность прогрессии
      n-количество членов арифм. прогр.

  • Дана арифметическая прогрессия, сумма её девяти первых членов равна 225. Найдите шестнадцатый член прогрессии, если её разность равна 3.


    Решение: Вот примерно решение представляем сумму 9 первых по формуле суммы так найдем а1 ну а дальше также по формуле находим а16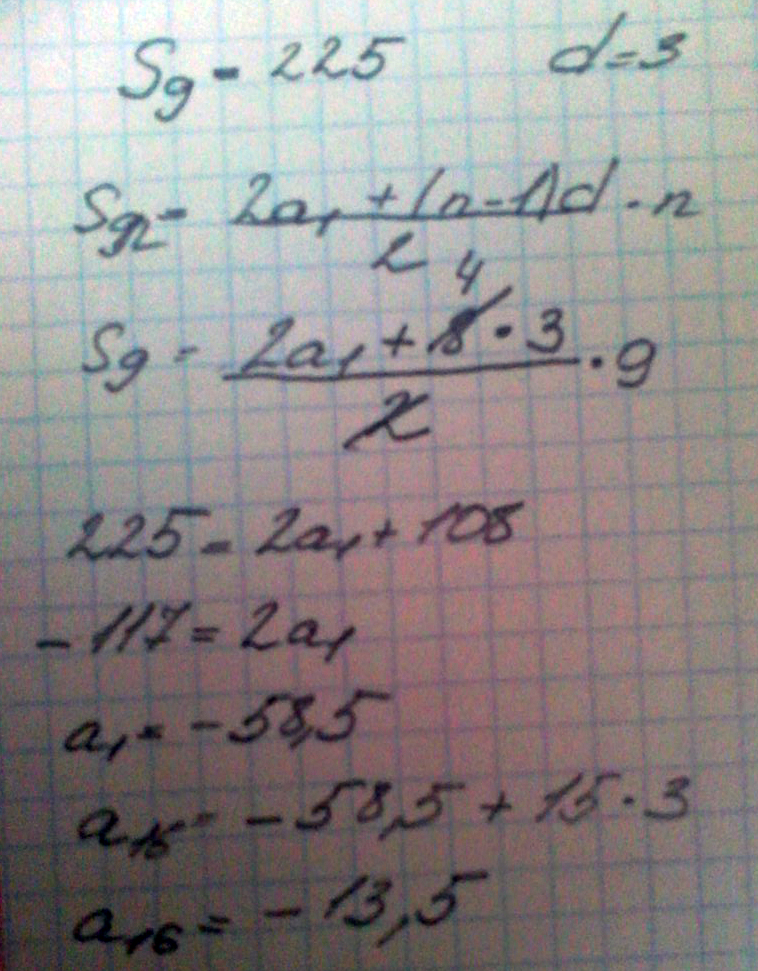 

    Вот примерно решение представляем сумму первых по формуле суммы так найдем а ну а дальше также по формуле находим а  ...

  • Разность арифметической прогрессии равна 4. Сумма семи первых членов равна 651. Найдите первый член этой прогрессии.


    Решение: У нас есть формула суммы арифметической прогрессии вида

    $$ S_{n}=\frac{2a_{1}+d(n-1)}{2}*n $$

    В эту формулу мы подставляем данные нам значения и находим первый член этой прогрессии. с уже подставленными в формулу значениями.

    Расписано:

    х+х+4+х+4+4+х+4+4+4+х+4+4+4+4+х+4+4+4+4+4+х+4+4+4+4+4+4= 651

    7x+84=651

    7x=567

    х=81

    Ответ: 81

    У нас есть формула суммы арифметической прогрессии вида S n frac a d n- n В эту формулу мы подставляем данные нам значения и находим первый член этой прогрессии. с уже подста...

  • В арифметической прогрессии сумма первого и девятого членов равна 64. Найдите разность между суммой ее 9 первых членов и пятым членом прогрессии.


    Решение: a1+a9 = 64

    a9 =a1 + (9-1) * d, a9 = a1 +8d, подставим в первую строчку вместо a 9

    a1 + a1 + 8d =64

    2a1 + 8d =64, разделим обе части равенства на 2. a1 + 4d =32

    Найдем сумму девяти членов:

    S9 = (2a1 + 8d) \2 *9= 64\2 * 9 =288

    Найдем пятый член:

    a5 = a1 +(5-1) * d = a1 + 4 d =32

    Найдем разность между суммой девяти членов и пятым членом:

    S9 - a5 = 288-32 = 256.

    Ответ. 256

<< < 789 10 11 > >>