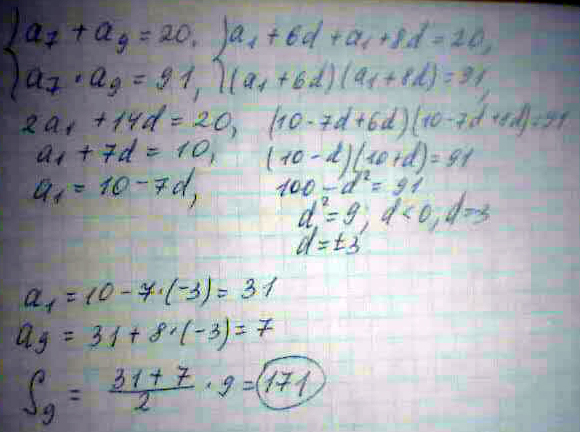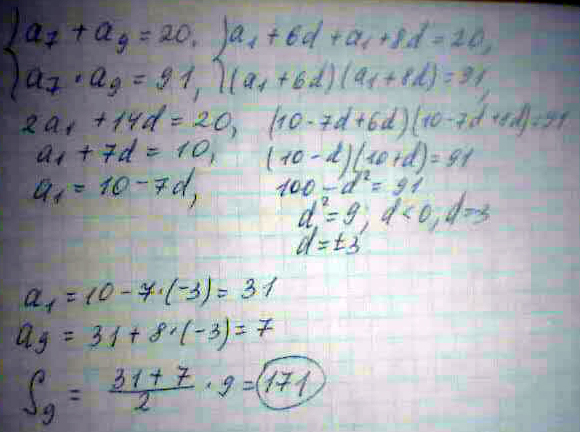разность членов арифметической прогрессии - страница 15
1) Является ли число 242 членом арифметической прогрессии аn=7n+4
2) Сумма третьего и пятого членов арифметической прогрессии равна 16, а шестой ее член на 12 больше второго. Найдите разность и первый член данной прогрессии
Решение: 1) an=7n+4242=7n+4
n=34 => является
2) a3+a5=16
a6-a2=12
a1+2d+a1+4d=16
a1+5d-a1-d=12
2a1+6d=16
4d=12
2a1+18=16
d=3
a1=-1
d=3
7n+4=242
7n=238
n=34
an=a1+d(n-1)
a6-a2=a1+d(6-1)-(a1+d(2-1))=a1+5d-a1-d=4d
4d=12
d=3
a3+a5=a1+d(3-1)+a1+d(5-1)=2a1+6d
2a1+6d=16
2a1+6*3=16
2a1+18=16
2a1=16-18
2a1=-2
a1=-1
Сумма утроенного второго и четвертого членов арифметической прогрессии равна 12. При каком значении разности прогрессии произведение третьего и пятого членов прогрессии будет наименьшим?
Решение: 3а2+а4=123(a1+d)+a1+3d=3a1+3d+a1+3d=4a1+6d=12
2a1+3d=6
a1=(6-3d)/2
a3*a5=(a1+2d)(a1+4d)= a1²+6a1d+8d² = (6-3d)²/4+6*d*( (6-3d)/2 )+8d²
(6-3d)²/4+6*d*( (6-3d)/2 )+8d²=0
(6-3d)²+12d(6-3d)+32d²=0
36-36d+9d²+72d-36d²+32d²=0
5d²+36d+36=0
Хвершины= -b/2a=-36/2*5=-3,6
То есть минимальное значение выражения а3*а5 достигается при d=-3,6
смотри вложения.
Сумма утроенного второго и четвёртого членов арифметической прогрессии равна 16. Определи, при каком значении разности прогрессии произведение третьего и пятого членов прогрессии будет наименьшем.
Ответ:
Разность прогрессии: d=
Решение: 3 * a₂ + a₄ = 16
3 * (a₁ + d) + a₁ + 3d = 16
4a₁ + 6d = 16
2a₁ + 3d = 8 -> 2a₁ = 8 - 3d
-
a₃ * a₅ = (a₁ + 2d)(a₁ + 4d) = a₁² + 6*a₁d + 8d²
((8 - 3d)² / 4) + (8 - 3d) * 3d + 8d² =
16 - 12d + (9d² / 4) + 24d - d² = (5d² / 4) + 12d + 16
парабола, ветви вверх,
наименьшее значение функции достигается в вершине параболы))
d₀ = -12 : (2*5/4) = -12*4/10 = -4.8
Сумма утроенного второго и четвёртого членов арифметической прогрессии равна 40. Вычисли, при каком значении разности прогрессии произведение третьего и пятого членов прогрессии будет наименьшем.
Решение: По условию задачи 3b<2> + b<4> =40, где b<2> и b<4> это соответственно, второй и четвертый члены прогрессии, отсюда, учитывая, что b<2> = b<1> + d
и b<4> = b<1> + 3d, получим b<1> = 10-1,5d
Рассмотрим функцию
f(d)= b<3> * b<5>= 8d +6b<1>d + (b<1>)^2=
=1,25d^2 +30d +100 Найдем производную функции f(d) и критические точки f’(d)=2,5d +30, f’(d)=0, d=-12
При переходе через критическую точку d=-12 производная меняет знак с - на +, т. о. при d=-12 произведение третьего и пятого членов прогрессии будет минимальнымРазность арифметической прогрессии является отрицательным числом. Найдите сумму девяти первых членов прогрессии, если сумма седьмого и девятого членов равна 20, а их произведение равно 91
Решение: Решение Вашего задания во вложенииS9 =?
{a7+a9=20
{a7*a9=91
{a7=20-a9
{(20-a9)a9 = 91
20a9-a9^2 = 91
-a9^2 +20a9 - 91= 0
D= 400-4*1*91 = 6^2
a9= -20+6/-2 = 7
a9 2 = -20-6/-2 = 13
a7=13
a7= 7
{a7=13
{a9=7
{a7=a1+6d =13
{a9=a1+8d = 7
{a1=13-6d
{13-6d+8d=7
{2d=-6
{d=-3
{a1=31
то есть разность отрицательно подходит!
S9 = (2a1+8d)/2* 9 = (62-24)/2 * 9 = 171