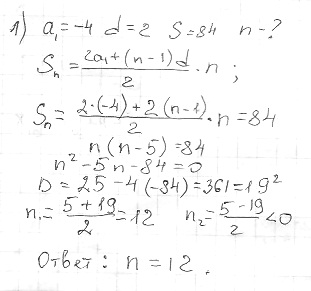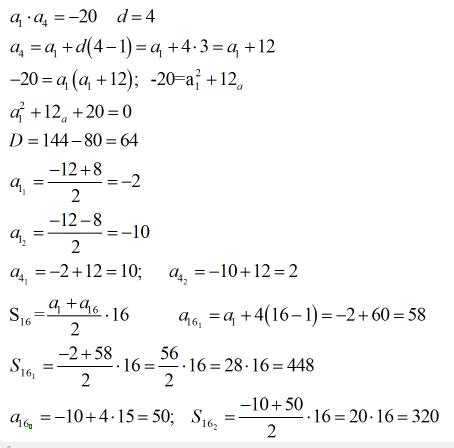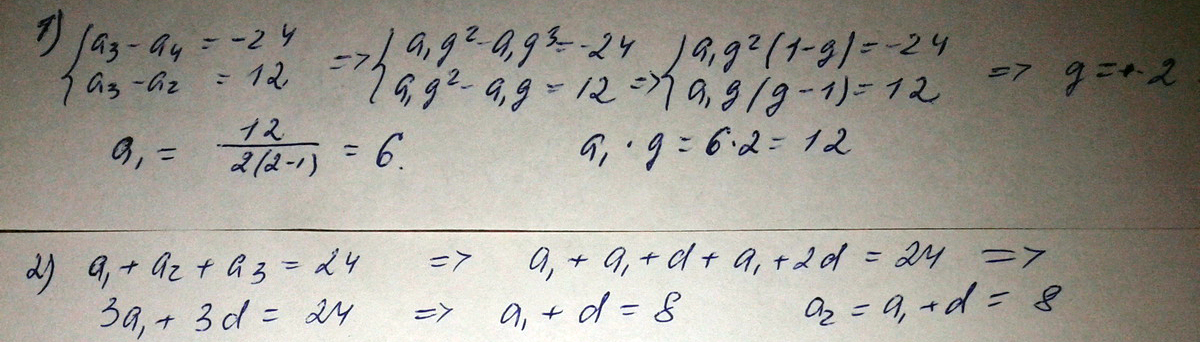прогрессия »

разность членов арифметической прогрессии - страница 17

  • Перший член арифметичної прогресії -4, а їх різниця дорівнює 2. Скільки требя взяти перших членів прогресії, щоб їх сума дорівнювала 84

    ________________________________

    первый член арифметической прогрессии 4, а их разность равна 2. Сколько нужно взять первых членов прогрессии, чтобы их сумма равнялась 84


    Решение: *перший член арифметичної прогресії -4, а їх різниця дорівнює 2. Скільки требя взяти перших членів прогресії, щоб їх сума дорівнювала 84

    Відповідь: треба взяти 12 перших членів даної арифметичної прогресії

    а₁=4

    d=2

    S=84

    4+6+8+10+12+14+16+18=88

    cо второго по 8 член

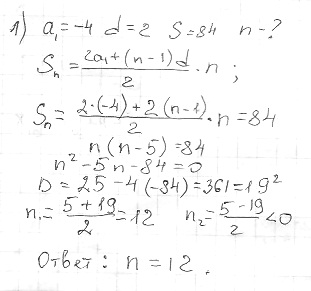
    перший член арифметично прогрес - а х р зниця дор вню . Ск льки требя взяти перших член в прогрес щоб х сума дор внювала В дпов дь треба взяти перших член в дано арифметично...

  • Произведение первого и четвёртого членов арифметической прогрессии равно -20, а разность прогрессии равна 4. Найдите сумму первых шестнадцати членов этой прогрессии.


    Решение: Формула 4 члена = a1+ 3d. Тогда a1 * (a1+3d) = -20 и d=4
    Найдем а1, а1² + 3da1=-20, подставим d a1² + 12a1=-20, получили квадратное уравнение. a1² + 12a1² +20=0,
    по Т. Виета a1 + a2 = -12
      a1*a2=20
    -10 И -2.
    Получается два решения. Для первого
    Сумма = (-10 + 4*15)*16\2 =400
    Для второго = (-2 + 4*15)*16\2 =  464
     

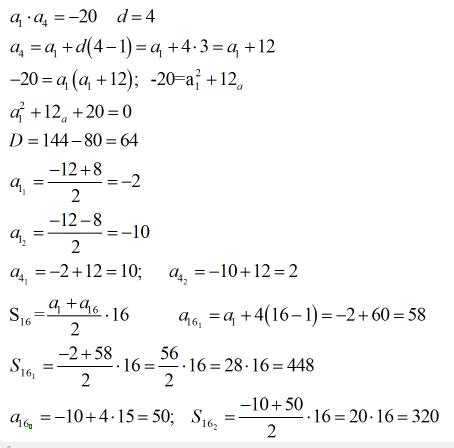
    Формула члена a d. Тогда a a d - и d Найдем а а da - подставим d a a - получили квадратное уравнение. a a по Т. Виета a a -   a a - И - .Получается два решения. Для первогоСу...

  • 1) разность третьего и четвёртого членов геометрической прогрессии равна -24, а разность третьего и второго членов равна 12. найдите произведение первого члена и знаменателя прогрессии
    2) сумма первых трёх членов арифметической прогрессии равна 24. найдите второй член прогрессии


    Решение: $$ 1.\;\begin{cases}b_3-b_4=-24\\b_3-b_2=12\end{cases}\\b_2=b_1\cdot q\\b_3=b_1\cdot q^2\\b_4=b_1\cdot q^3\\\begin{cases}b_1\cdot q^2-b_1\cdot q^3=-24\;\;\;\;\times-1\\b_1\cdot q^2-b_1\cdot q=12\end{cases}\Rightarrow\begin{cases}q\cdot\left(b_1\cdot q^2-b_2\cdot q\right)=24\\b_1\cdot q^2-b_1\cdot q=12\end{cases}\Rightarrow\\\Rightarrow\begin{cases}12q=24\\b_1\cdot\left(q^2-q\right)=12\end{cases}\Rightarrow\begin{cases}q=2\\b_1\cdot(4-2)=12\end{cases}\\2b_1=12\Rightarrow b_1=6 $$
    $$ \begin{cases}q=2\\b_1=6\end{cases}\\b_1\cdot q=b_2=2\cdot6=12 $$
    $$ 2.\;a_1+a_2+a_3=24\\a_1+\left(a_1+d\right)+\left(a_1+2d\right)=24\\3a_1+3d=24\\3(a_1+d)=24\\a_1+d=a_2=8 $$

    .

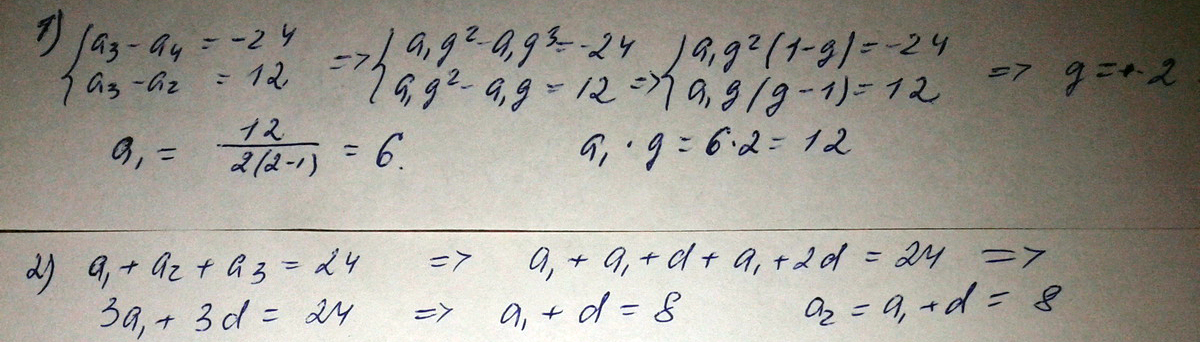
    . begin cases b -b - b -b end cases b b cdot q b b cdot q b b cdot q begin cases b cdot q -b cdot q - times- b cdot q -b cdot q end cases Rightarrow begin cases q cdot left b...

  • 1) в арифметической прогресси (An): A17=7.27, A21= -4.73, Найдите разность арифметической прогресси

    2) в арифметической прогресси (Cn) C1= -4, а сумма первых девяти её членов равна 72. найдите разность ар. прогрес.


    Решение: 1) разность находим по формуле d=Am-Ak/m-k

    тогда получимd=21-17/-4/73-7.27

                               d=4/-12

                               d=-1/3

    2) из формулы сумма  арифметической прогресси получаем:S=A1+An*n/2

                                                                                                                       72=-4+9*n/2

                                                                                                                       n=28,8

    разность находим по формуле d=Am-Ak/m-k

    тогда получимd=9-1/28,8-(-4)

                               d=8/32,8

                               d=0,24, если округлить примерно получим 0,25

  • 1) найдите разность арифметической прогрессий, если: a1=-5, n=23, Sn=1909
    2) найдите десятый член и значения суммы десяти первых членов арифметической прогрессий -3,87; -2,77.;
    3) найдите разность арифметической прогрессий, если: a2=2, a9=6,9
    4) арифметическая прогрессия (Хn) задана формулой: 1) Xn=3n+2. Найдите значение суммы двадцати первых ее членов; 2) Xn=4n-9. найдите значение суммы тридцати первых ее членов;
    5) найдите a1 и n, если: 1) d=2, an=49, Sn=702 2) an=18-2n иSn=n*(17-n).


    Решение: Формулы n-го члена и суммы n членов известны
    an = a1 + d*(n - 1)
    S(n) = (a1 + an)*n/2 = (2a1 + d*(n-1))*n/2
    1) a1 = -5, n = 23, S(n) = 1909
    1909 = (-2*5 + d*22)*23/2 = (-5 + 11d)*23
    -5 + 11d = 1909/23 = 83
    11d = 88, d= 8
    2) a1 = -3,87, d= -2,77 + 3,87 = 1,1, n = 10
    a10 = a1 + 9d = -3,87 + 9*1,1 = 9,9 - 3,87 = 6,03
    S(10) = (-3,87 + 6,03)*10/2 = 2,16*5 = 10,8
    3) a2 = a1 + d= 2, a9 = a1 + 8d = 6,9
    a9 - a2 = 7d = 6,9 - 2 = 4,9
    d= 0,7
    4) 1) x1 = 3 + 2 = 5, x2 = 6 + 2 = 8, d= 3
    S(20) = (2*5 + 3*19)*20/2 = (10 + 57)*10 = 670
    2) x1 = 4 - 9 = -5, x2 = 8 - 9 = -1, d= 4
    S(30) = (-2*5 + 4*29)*30/2 = (-10 + 116)*15 = 1590
    5) 1) d= 2, an = 49, S(n) = 702
    Система
    { an = a1 + d(n-1) = a1 + 2(n-1) = 49
    { S(n) = (a1 + an)*n/2 = (a1 + 49)*n/2 = 702
    { a1 + 2n = 49 + 2 = 51
    { a1*n + 49n = 702*2 = 1404
    { a1 = 51 - 2n
    { (51 - 2n)*n + 49n - 1404 = 0
    -2n^2 + 100n - 1404 = 0
    n^2 - 50n + 702 = 0
    (n - 27)(n - 13) = 0
    n = 13, a1 = 51 - 26 = 25
    n = 27, a1 = 51 - 54 = -3
    2) an = 18 - 2n, S(n) = n*(17 - n)
    an = a1 + d(n-1) = a1-d + dn = 18 - 2n
    S(n) = (2a1 + d(n-1))*n/2 = n*(17 - n)
    Система
    { (a1-d) + dn = 18 - 2n
    { (2a1-d) + dn = 2(17 - n) = 34 - 2n
    Из 2 уравнения вычитаем 1 уравнение
    a1 = 34 - 18 = 16
    Подставляем обратно в 1 уравнение
    16 + dn - d = 18 - 2n
    dn - d = 2 - 2n
    d(n - 1) = -2(n - 1)
    d= -2
<< < 151617 18 19 > >>