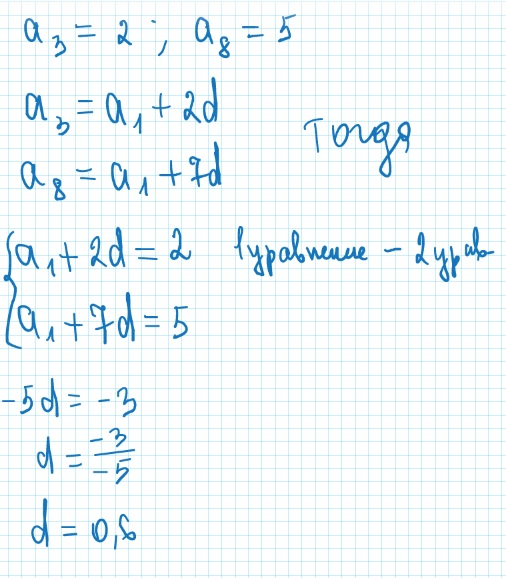прогрессия »

разность членов арифметической прогрессии - страница 19

  • Найдите разность арифметической прогрессии, если ее третий и восьмой члены равны 2 и 5


    Решение: An=a1+d(n-1) a3=2 n=3 a8=5 n=8 a3=a1+d(n-1)=a1+d(3-1)=a1+2d a8=a1+d(n-1)=a1+d(8-1)=a1+7d a3-a8=a1+2d-a1-7d a3-a8=-5d 2-5=-5d -3=-5d|:(-5) d=3/5 d=0,6

    $$ a_{3} =2; a_{8} =5 $$
    $$ a_{3} = a_{1} +2d =2; a_{8} = a_{1} +7d=5 $$
    $$ \left \{ {{ a_{1}+2d=2} \atop {a_{1}+7d=5}} \right.;\left \{ {{ a_{1}=2-2d} \atop {2-2d+7d=5}} \right.;\left \{ {{ a_{1}=2-2d} \atop {5d=3}} \right.;\left \{ {{ a_{1}=2-2d} \atop {d=3/5}} \right.;\left \{ {{ a_{1}=2-2(3/5)} \atop {d=3/5}} \right.;\left \{ {{ a_{1}=4/5} \atop {d=3/5}} \right. $$

  • Найдите разность арифметической прогрессии, если ее третий и восьмой члены равны 2 и 5 соответственно


    Решение: An= a1+d*(n-1)
    a3 = a1+d*(3-1)=a1+ 2d
    a8 = a1+d*(8-1)=a1+7d
    a1+2d = 2 (1)
    a1+7d = 5 (2)
    (2)-(1): 7d-2d = 5-2
    5d = 3
    d= 3/5
    d =0,6

    Арифметическая прогрессия

    An a d n- a a d - a da    a d - a da d a d    - d- d - d d d Арифметическая прогрессия...

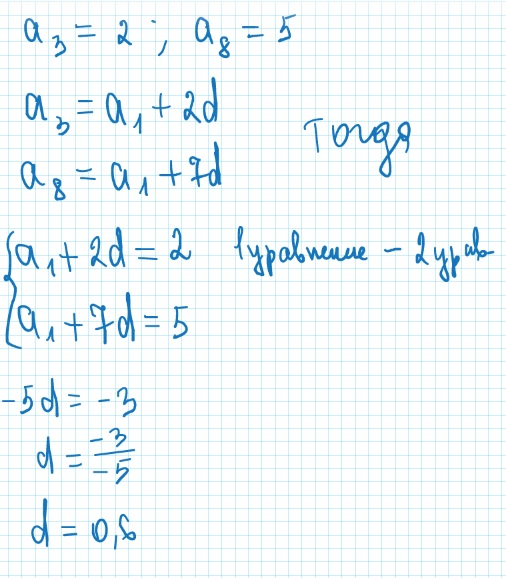
  • 6. Между числами 97 и 73 вставьте 5 чисел так чтобы полученная последовательность была арифметической прогрессией
    1. найдите разность и последний член арифметической прогрессии a n если a1=4, S8=-108


    Решение: 6. Между ними разность 97 - 73 =24  - вставить 5 чисел значит промежутков на один больше = 6.
    Разность - 24/6 = 4 - делим на число промежутков
    Числа будут 97 - 93 89 85 81 77 - 73
    Задача 1.
    Сумма 8 членов = 8*4+(1+2+3+4+5+6+7)*R= -108
    или -108-32 = 28*R= 140 Отсюда R=-5
    Последний член = а(8) =а1+7*R = 4+ 7*(-5) = -31
    Ответ R= -5, a8= -31

  • В Арифметической прогрессии Sn- сумма первых n ее членов. Найдите разность прогрессии если А5=9, S10= 100


    Решение: $$ a_5=9 $$
    $$ S_{10}=100 $$
    $$ a_n=a_1+(n-1)*d $$
    $$ S_n=\frac{2a_1+(n-1)*d}{2}*n $$
    $$ a_1+(5-1)*d=9 $$
    $$ \frac{2a_1+(10-1)*d}{2}*10=100 $$
    $$ a_1+4d=9 $$
    $$ (2a_1+9d)*5=100 $$
    $$ 2a_1+8d=18 $$
    $$ 2a_1+9d=20 $$
    $$ d=(2a_1+9d)-(2a_1+8d)=20-18=2 $$
    отвте: 2

  • сумма пятого и восьмого членов арифметической прогрессии на 15 больше суммы седьмого и десятого. Найдите разность прогрессии


    Решение: Формула для n-го члена арифметической прогрессии имеет вид:

    аn = a₁ + d(n - 1)

    Тогда

    а₅ = a₁ + 4d

    а₈ = a₁ + 7d

    Их сумма

    а₅ + а₈  =  2a₁ + 11d

    а₇ = a₁ + 6d

    а₁₀ = a₁ + 9d

    Их сумма

    а₇ + а₁₀  =  2a₁ + 15d

    По условию

    а₅ + а₈ - 15 = а₇ + а₁₀

    2a₁ + 11d - 15 = 2a₁ + 15d

    4d = -15

    d = -3,75

    Ответ: разность арифметической прогрессии d = -3,75

    Выразим данные нам члены прогрессии через седьмой, по определению арифметической прогрессии:

    a5 = a7 - 2d, a8 = a7 + d, a10 = a7 + 3d,

    тогда уравнение примет вид:

    a7 - 2d + a7 + d = a7 + a7 + 3d + 15, =>

    => 2a7 - d = 2a7 + 3d + 15 => -4d = 15 => d = -3, 75

    Ответ: -3, 75

<< < 171819 20 21 > >>