неравенства »
решите неравенство - страница 7
Найдите все значения а, для каждого из которых неравенство ах в квадрате -4х+3а+1>0 выполняется для всехх>0.
Решение: Ax^2-4x+3a+1>0 для всех x>0
геометрическая интерплетация данного неравенства означает, что парабола лежит выше оси Х, для этого нужно, чтобы выполнялось 2 условия a>0 , D<0
D(половинный)=(-2)^-a(3a+1)=4-3a^2+a
-3a^2-a+4<0
3a^2+a-4>0 3a^2+a-4=0 D=1+4*3*4=49 a1=1 a2=-4/3 3a^2+a-4=3(a+4/3)(a-1)=(3a+4)(a-1)
(3a+4)(a-1)>0
a=-4/3 a=1 отметитм на прямой Х и расставим знаки на интервалах
-4/3 1
+ - +
объединяем с a>0 ⇒ a∈(1,+00)Найдите все значения а, для каждого из которых неравенство ах2 -4х+3а+1>0 выполняется для всех х.
Решение: Ax²-4x+(3a+1)>0
D=16-4a(3a+1)<0
12a²+4a-16>0
3a²+a-4>0
D=1+48=49
a1=(-1-7)/6=-4/3
a2=(-1+7)/6=1
+ _ +
____________________________________
-4/3 1
a∈(-∞;-4/3) U (1;∞)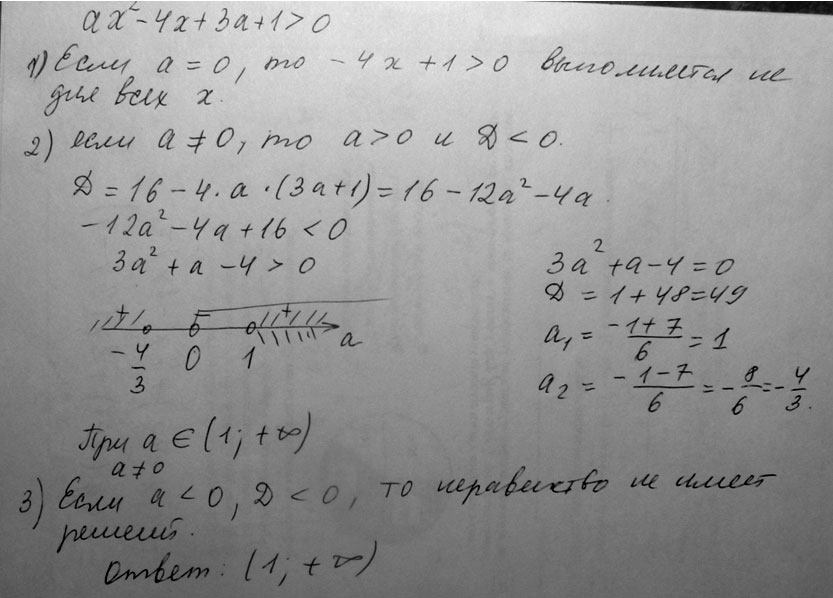
Найдите все положительные значения "а", для каждого из которых неравенство
ах^2 - (а^2 - 5а+6)х - 5а^2 +6а ≥ 0 выполняется для любого "х"
Решение: Налицо квадратное неравенство
Мы знаем, что квадратное неравенство выполняется для любого икс, если его дискриминант меньше нуля
Считаем дискриминант
D=b^2-4ac = (a^2-5a+6)^2-4a*(-5a^2+6a) = (a^2+5a-6)^2
Тут получился полный квадрат, так что в принципе можно было и красиво решить это неравенство, но у нас задача иная
Решаем неравенство
(a^2+5a-6)^2 < 0
Это неравенство решений не имеет, ибо квадрат числа не может быть меньше нуля
Значит, таких "а" нетНайти значения параметра a, для каждого из которых неравенство, верно при всех значениях x, $$ \log_{\frac{a(a-2)}{8}}(2^x + \frac{a^2}{2^x}) \ge 1 $$
Решение: 1) Если основание логарифма
0 < a(a - 2)/8 < 1
0 < a^2 - 2a < 8
{ a(a - 2) > 0
{ a^2 - 2a - 8 = (a - 4)(a + 2) < 0
Получается
{ a < 0 U a > 2
{ a < -2 U a > 4
Область определения: a < -2 U a > 4
При этом функция логарифма - убывающая. Тогда
2^x + a^2/2^x <= a(a - 2)/8
Замена 2^x = y > 0 при любом х
y + a^2/y - a(a - 2)/8 <= 0
(8y^2 - a(a - 2)*y + 8a^2) / y <= 0
y > 0 при любом х, поэтому
8y^2 - (a^2 - 2a)*y + 8a^2 <= 0
Это неравенство не может быть верно при любом y, только на отрезке (y1; y2)
Значит, если 0 < a(a - 2)/8 < 1, то решений нет.
2) Если основание
a(a - 2)/8 > 1
a^2 - 2a > 8
a^2 - 2a - 8 > 0
(a - 4)(a + 2) > 0
Область определения: a < -2 U a > 4
При этом функция логарифма - возрастающая. Тогда
2^x + a^2/2^x >= a(a - 2)/8
Замена 2^x = y > 0 при любом х
y + a^2/y - a(a - 2)/8 >= 0
8y^2 - (a^2 - 2a)*y + 8a^2 >= 0
D = (a^2 - 2a)^2 - 4*8*8a^2 = a^4 - 4a^3 + 4a^2 - 256a^2 = a^4 - 4a^3 - 252a^2
Если это верно при любом х (и при любом у), то D < 0
a^4 - 4a^3 - 252a^2 < 0
Делим все на a^2 > 0
a^2 - 4a - 252 < 0
D/4 = 4 + 252 = 256 = 16^2
a1 = 2 - 16 = -14; a2 = 2 + 16 = 18
Решение: (-14, 18)
С учетом области определения: a < -2 U a > 4
Ответ: (-14; -2) U (4; 18)Найдите все значения параметров b для каждого из которых неравенство (b+2)x^2-(b+1) x +2>0 выполняется при любых дейсьветительных знаенияхx
Решение: В заданном неравенстве (b+2)x^2-(b+1) x +2>0 левая часть - квадратный трёхчлен. Его общий вид: ах²+вх+с.
Пусть f(x) = ax² + bx + c, a ≠ 0.
Для того, чтобы корни данного квадратного трёхчлена были больше некоторого числа t, необходимо и достаточно, чтобы выполняласьследующая система условий: D ≥ 0,a · f(t) > 0,x₀ > t (это абсцисса вершины параболы, t = 0 по заданию).
Находим дискриминант: D=b²-4ac.
D=b²+2b+1-4(b+2)*2 = b²-6b-15.
Приравниваем его нулю: b²-6b-15 = 0.
Квадратное уравнение, решаем относительно b:
Ищем дискриминант:D=(-6)^2-4*1*(-15)=36-4*(-15)=36-(-4*15)=36-(-60)=36+60=96;
Дискриминант больше 0, уравнение имеет 2 корня:b₁=(√96-(-6))/(2*1)=(√96+6)/2=√96/2+6/2=√96/2+3 = 2√6+3 ≈ 7.89898;
b₂=(-√96-(-6))/(2*1)=(-96+6)/2= -96/2+6/2=- √96/2+3 = -2√6+3 ≈ -1.89898.
Находим a · f(t):
f(0) = (b+2)*0²-(b+1)*0+2 = 2.
a · f(t) = (b+2)*2 = 2b+4.
Находим условие a · f(t) > 0:
2b+4 > 0,
2b > -4,
b > -2.
Проверяем третье условие: x₀ > t.
x₀ = -b/2а = (b+1)/(2b+4) > 0.
b > -1.
Совместное выполнение всех условий даёт ответ:
чтобы неравенство (b+2)x^2-(b+1) x +2>0 выполнялось при любых действительных значениях x, параметр b должен находиться на отрезке:
3-2√6 < b < 3+2√6.

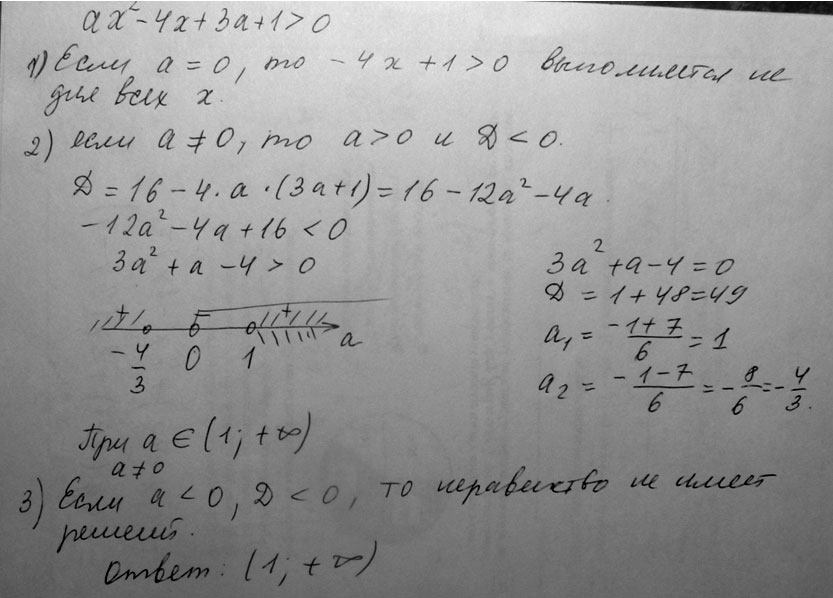
 Если числа a и b равны между собой, то a - b = 0. Если же числа a и b не равны между собой, то разность a - b либо положительна, либо отрицательна.
Если разность a - b положительна, то говорят, что число a больше числа b; записывается это таким образом:
a > b. (1)
Если разность a - b отрицательна, то...
Если числа a и b равны между собой, то a - b = 0. Если же числа a и b не равны между собой, то разность a - b либо положительна, либо отрицательна.
Если разность a - b положительна, то говорят, что число a больше числа b; записывается это таким образом:
a > b. (1)
Если разность a - b отрицательна, то... Линейные неравенства
Так называются неравенства, левая и правая части которых представляют собой линейные функции относительно неизвестной.величины. К ним относятся, например, неравенства
2x - 1 > - x + 3; 7x 4 - 6x; 9 - x < x + 5
и т. д. Для определенности мы рассмотрим лишь неравенства, содержащие знак >. Линейное неравенство, содержащее знак >, имеет вид:
ах + b >...
Линейные неравенства
Так называются неравенства, левая и правая части которых представляют собой линейные функции относительно неизвестной.величины. К ним относятся, например, неравенства
2x - 1 > - x + 3; 7x 4 - 6x; 9 - x < x + 5
и т. д. Для определенности мы рассмотрим лишь неравенства, содержащие знак >. Линейное неравенство, содержащее знак >, имеет вид:
ах + b >...