при каких значениях дробь не имеет смысла - страница 18
При каких значениях и имеет смысл выражение? 5b делим на (2минус дробь в числители 4, в знаменателе3-2b) чтобы в ответе было 0,5 и 1,5
Решение: 5В/2 - 4/3-2В?Тогда, если это так, то выражение будет иметь смысл в том случае, когда в дроби знаменатель не равен нулю, следовательно мы сразу же можем написать условие, что
3-2В не должно быть равно 0, следовательно В не должно быть равно 1,5-первый ответ.
Откуда может взяться 2-ой корень, ведь в знаменателе первой дроби стоит просто число, без какой-либо переменной! Вы уверены, что там должно быть 2 ответа?
При каких значениях X имеет смысл выражение под корнем 1-x дробь x+2
Решение: Все мы знаем, что на 0 делить нельзя.
Следовательно, выражение x+2 не должно равняться нулю. Оно будет равняться нулю лите в случае, когда x=-2.
Так же мы, конечно, в курсе, что корень из отрицательного числа не извлекается. Когда выражение 1-x/x+2 будет отрицательным? В случае, когда x<=1 и x+2>-2.
Ещё раз. Выражение не имеет смысл при
x=-2. и x<-2 и x<=1
То есть при следующих значения функция имеет место быть:
(-2;1]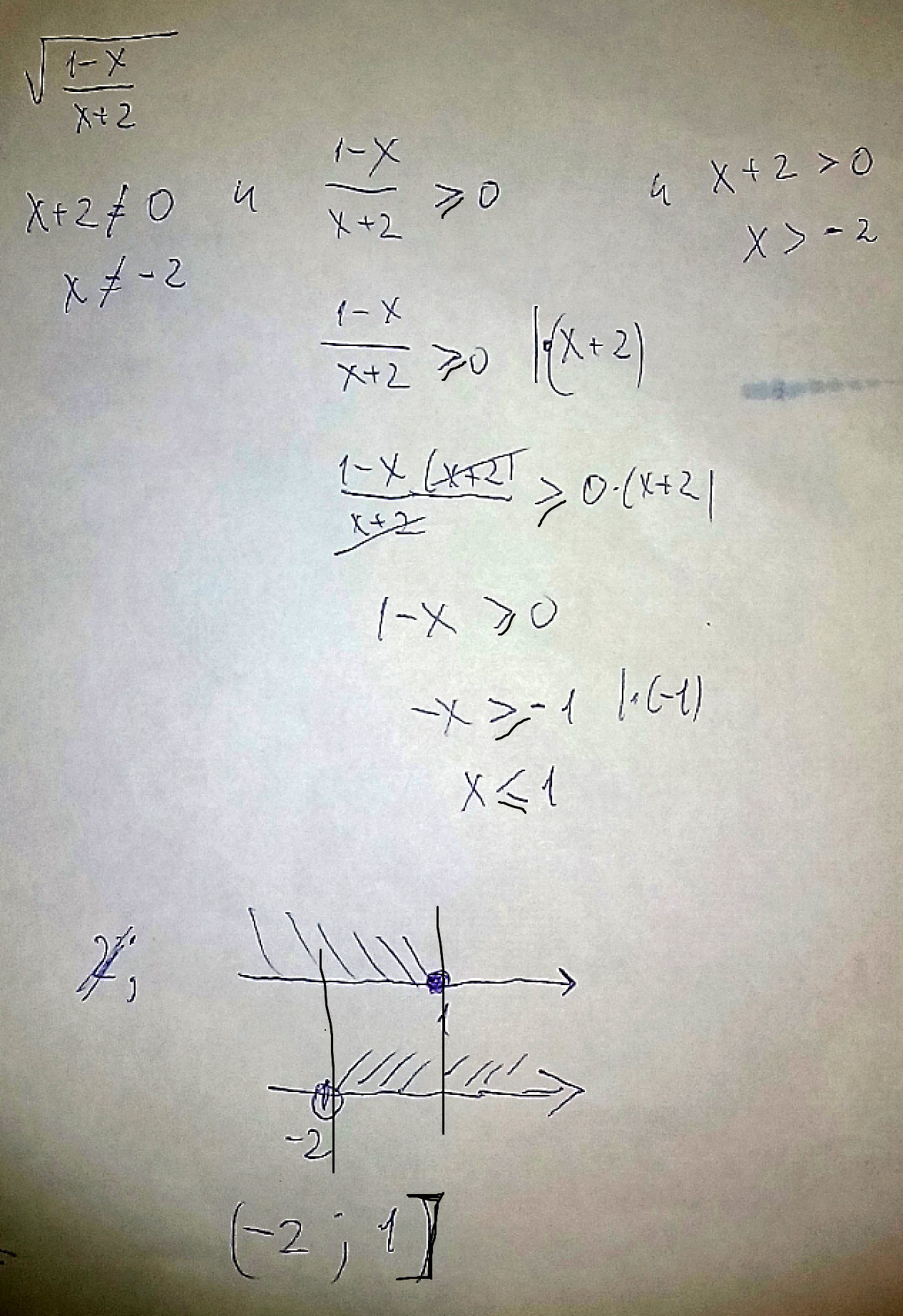
1) Найдите корни квадратного трехчлена:
а)x^2+5x-24
б)3x^2-19x-14
2) Выделите из трехчелена квадрат двучелена:
а)x^2-14x+49
б)x^2+5x-6
в)3x^2-18x-15
3) Докажите, что при любом значении x трехчелен:
а)x^2-4x+31 принимает положительных значения.
б)9x^2+24x+16 принимает неотрицательные значения
4) При каком значении x трехчлен принимает наибольшее значение?
а)-(x+2)^2+5
б)-x^2+5x-4
в)-3x^2-9x+15
5) Разложите на множители квадратный трехчелен:
а)4x^2-x
б)x^2+7x+10
в)5x^2-7x+2
г)-2x^2-9x-9
6) Сократите Дробь
а)(x^2-2x-15)/(x^2+6x+9)
б)(2m^2-3m-5)/(4m-12m+5)
в)(a^2-a^2-a+1)/(a^2-2a+1)
7) Постройте график функции
y=(x^2-7x+12)/(x-4)
8) При каких значениях k трехчлен 4kx^2-5x+25k нельзя разложить на линейные множители?
Решение: 1)
а) Д= 25+96=121
x1= (-5+11)/2=3
х2= (-5-11)/2=-13
б) Д= 361+168=529
х1= (19+23)/6=7
х2=(19-23)/6= 4/6
2)a) x^2 -14x +49 = (x-7)^2
б) x^2 + 5x -6 = (x+5)^2 -5x -31
в)
3)x^2 -4x +31>0
Д=16-4*31 < 0 => нету пересечения с осью ox, т. к. ветви вверх, то всегда >0
б) 9x^2 +24x +16
Д= 576-576=0 => 1 т. пересечения с осью ox, ветви вверх => >=0
5) 4x^2 -x = x(4x-1)
б) x^2 +7x+10
Д=49-40=9
x1= -7+3/8= -1/2
x2= -5/4
x^2+7x+10=(x+1/2)(x+5/4)
В) 5x^2 - 7x +2
Д= 49-40=9
x1 = 7+3/10=1
x2= 7-3/10= 4/10=0,4
5x^2 - 7x +2 = 5(x-1)(x-0,4) про 5 не уверен
Г) -2x^2-9x-9=2x^2 + 9x +9
Д=81-72=9
x1= -9-3/4=-3
x2=-9+3/4= -6/4
2x^2 + 9x + 9 = 2(x+3)(x+6/4) про 2 не уверен :CУпростите выражение:
\( \frac{1+cos(2x+\frac{\pi}{6})}{(1+\sqrt{3})cosx-(\sqrt{3}-1)sinx} \)
Существует ли какое-нибудь значение переменной, при котором данное выражение равно нулю?
Пять различных чисел соствалют арифметическую прогрессию. Если удалить ее второй и третий члены, то три оставшихся числа составят геометрическую прогрессию. Найдите ее знаменатель.
Сократите дробь
\( \frac{x+169}{\sqrt{-x}+13} \)
Решение: $$ \frac{1+cos(2x+\pi/6)}{(1+\sqrt3)cosx-(\sqrt3-1)sinx}=\frac{2cos^2(x+\pi/12)}{(sinx+cosx)-\sqrt3(sinx-cosx)}= \\ =\frac{2cos^2(x+\pi/12)}{\sqrt2sin(x+\pi/4)+\sqrt6cos(x+\pi/4)}=\frac{2cos^2(x+\pi/12)}{2\sqrt2sin(x+\pi/4+\pi/3)}= \\ =\frac{cos^2(x+\pi/12)}{\sqrt2cos(x+\pi/12)}=\frac{\sqrt2cos(x+\pi/12)}{2}. $$Данное выражение равно 0, когда:cos(x+П/12)=0, или х = 5П/12 + Пк.
2. Из условия:
b1 = a1
b2 = a1 + 3d,
b3 = a1+4d
С другой стороны: b2 = b1q, b3 = b1q^2. Получим следующую систему:
a1+3d = a1q, a1(q-1) = 3d
a1+4d = a1q^2 a1(q^2 -1) = 4d Делим второе уравнение на первое:
q+1 = 4/3 или q = 1/3.
Ответ: 1/3.
3. Пусть t = кор(-х)
$$ \frac{169-t^2}{13+t}=13-t=13-\sqrt{-x} $$
1) запишите дробь при сокращении которой следует указать что а не равно 2
2) какие значения х не являются допустимыми для выражения х+5/16-x^2
3) сократите дробь 8x^3-1/1-4y^2
Решение: 1) $$ \frac{6}{a-2} $$, a ≠ 2, т. к. если будет а = 2, то знаменатель станет = 0, а на 0 делить нельзя
2) $$ \frac{x+5}{16-x^2}= \frac{x+5}{(4-x)*(4+x)} $$
x ≠ -4 и х ≠ 4, в обратном случае знаменатель будет равен 0, а на ноль делить нельзя
3) $$ \frac{8x^3-1}{1-4y^2}= \frac{(2x-1)*(4x^2+2x+1)}{(1-2y)*(1+2y)} $$ данную дробь сократить нельзя, т. к. переменные х и у - разные числа (в условии задания не сказано, что х = у)

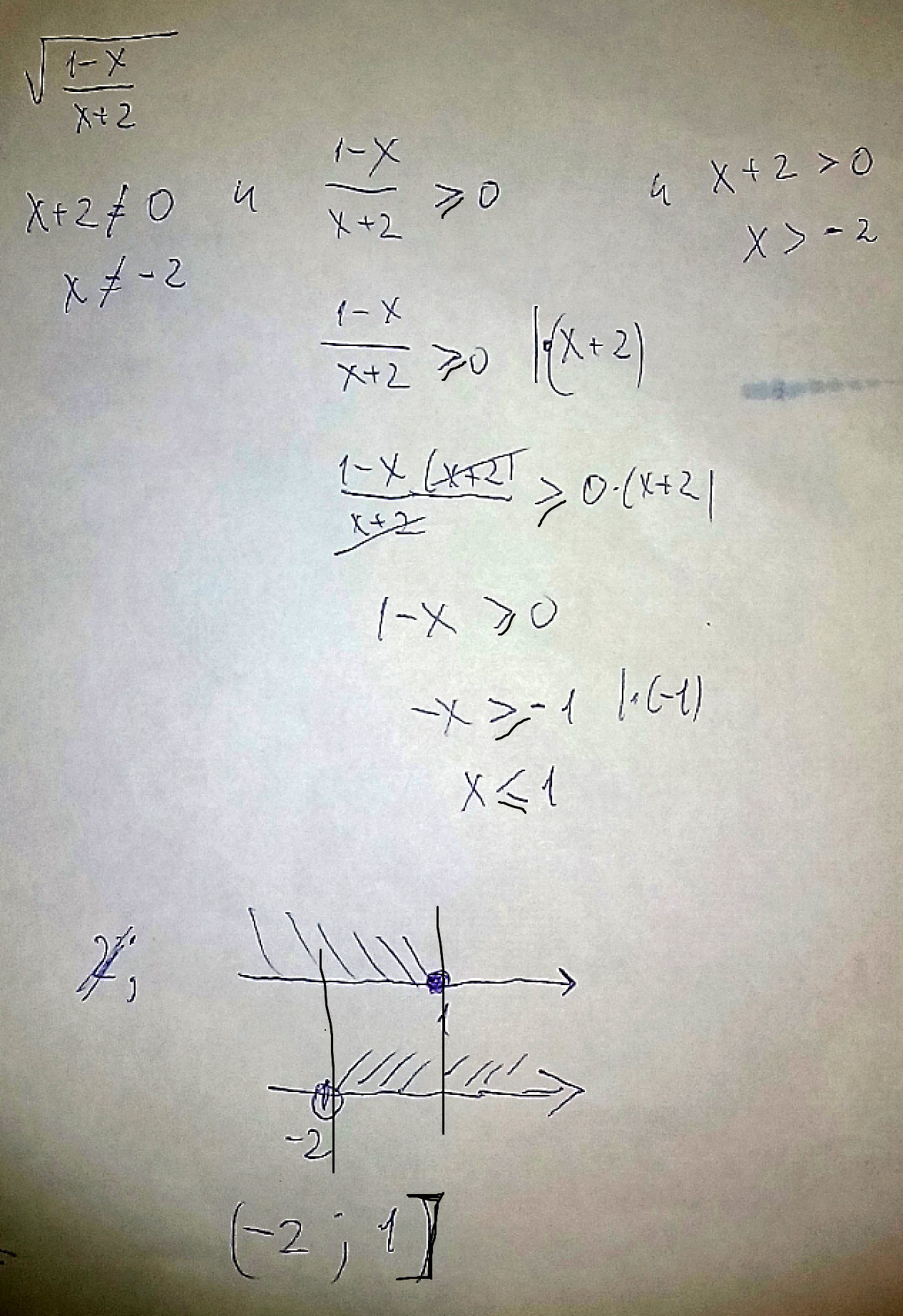
 Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...
Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...