дроби »
разложите на множители числитель и знаменатель дроби - страница 15
Решите уравнения методом разложения на множители
cos x = 3 sin x cos x
Решение: cos x = 3 sin x cos x
3 sinx * cosx - cos x =0
cosx(3 sinx - 1)=0
cosx=0 или 3sinx -1 =0
x= π/2+πn 3sinx= 1
3sinx= π/2+2πn
x= π/6+πn/3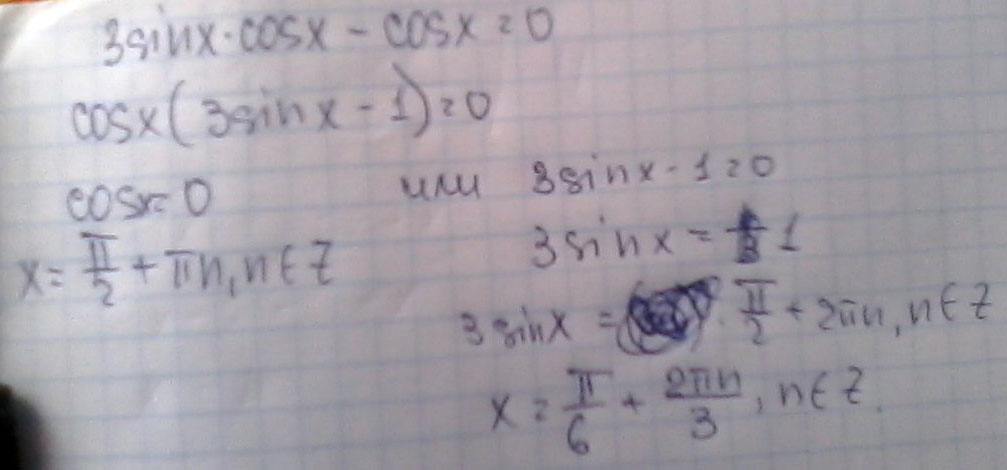
Решение алгебраических уравнений разложением на множители: 2x^5-x^4-12x^3+6x^2+18x-9=0
найти корни
Решение: x⁴ (2x - 1) - 6x²(2x - 1) + 9(2x-1) = 0
(2x-1)(x⁴ - 6x² + 9) =0
x⁴ - 6x² + 9 =0 или 2x-1=0
x² = a 2x=1
a² - 6a +9=0 x = 1/2
D₁= 9 -9=0
a = 3
x² = 3
x = +-√3
Ответ: √3; -√3; 1/2
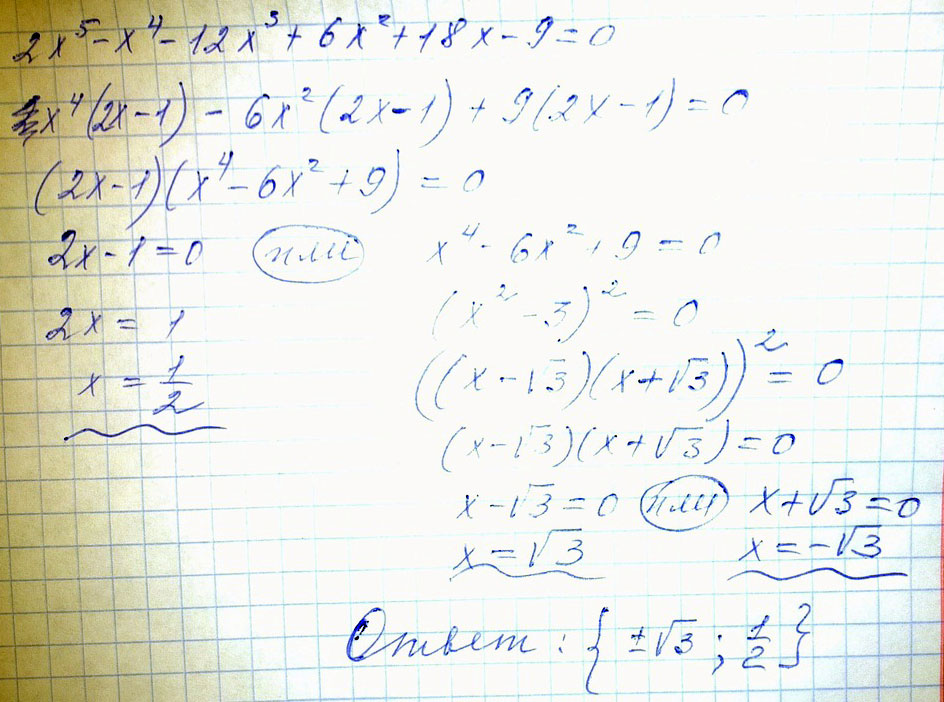
Задания на разложения на множители: ab+3c+cd+3a
10x+ab+10a+bx
2c+2b-xc-xb
3x+3y-ax-ay
mn+kn-5m-5k
4a-dc-ab+4c
x-ay-ax+y
Решение: аb+3с+сd+3a= (ab+3a)+(3c+cd)=a(b+3)+c(3+d)= (b+3)(a+c)10x+ab+10a+bx=(10x+bx)+(ab+10a)=x(10+b)+a(b+10)=(10+b)(x+a)
2c+2b-xc-xb=(2c-xc)+(2b-xb)=c(2-x)+b(2-x)=(2-x)(c+b)
3x+3y-ax-ay=(3x-ax)+(3y-ay)=x(3-a)+y(3-a)=(3-a)(x+y)
mn+kn-5m-5k=(mn-5m)+(kn-5k)=m(n-5)+k(n-5)=(n-5)(m+k)
4a-bc-ab+4c=(4a-ab)+(-bc+4c)=a(4-b)-c(b-4)= -(4-b)(a-c)
x-ay-ax+y=(x-ax)+(-ay+y)=x(1-a)-y(a-1)= -(1-a)(x-y)
Решите уравнения, используя разложения на множители:
1.(2x-9)(x+6)-x(x+6)=0
2.(3x+4)(x-10)+(10-x)(x-8)=0
3.3(3x +1 )<2 - 4 (3x+1)=0
4.(9x-12)-x(9x-12)=0
Решение: 1)
(2х-9)(х+6)-х(х+6) = 0
(х+6)(2х-9-х) = 0
(х+6)(х-9) = 0
х+6=0, или х-9=0
х=-6, или х=9
Ответ: -6; 9 (два ответа).
2)
(3х+4)(х-10)+(10-х)(х-8) = 0
(х-10)(3х+4-х+8) = 0
(х-10)(2х+12) = 0
х-10=0, или 2х+12=0
х=10, или х=-6
Ответ: 10; -6.
4)
(9х-12)-х(9х-12) = 0
(9х-12)(1-х) = 0
9х-12=0, или 1-х=0
9х=12, или х=1
х= \(1\frac{1}{3}\)
Ответ:\(1 \frac{1}{3}\); 1.Решить уравнение методом разложения на множители.
1) \( \sqrt{3} cosx= sin^2x*cosx \)
2) \( 2sin \frac{x}{y} = 3sin^2 \frac{x}{y} \)
3) \( sin2x= \sqrt{2} sinx \)
4) \( \sqrt{2} cos^24x+cos4x=0 \)
Решение: 1) √3cosx-sin²x cosx=0 cosx(√3-sin²x)=0 cosx=0 x=π/2+πn
sin²x=√3 корней не имеет
3) 2cosx sinx-√2sinx=0
sin x(2cosx-√2)=0 sinx=0 x=πn. n∈z
2cosx=√2 cosx=√2/2 x=+-π/4+2πk. k∈z
4) cos 4x(√2cos 4x+1) cos 4x=0 4x=π/2+πn x=π/8+πn/4
√2cos4x=-1 cos 4x=-1/√2 4x= +-3π/4+2πk x=+-3π/16+πk/2

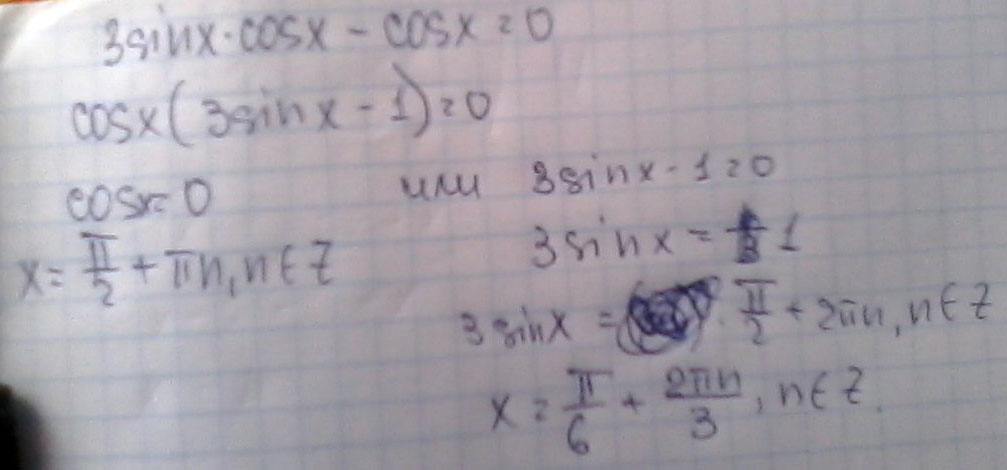
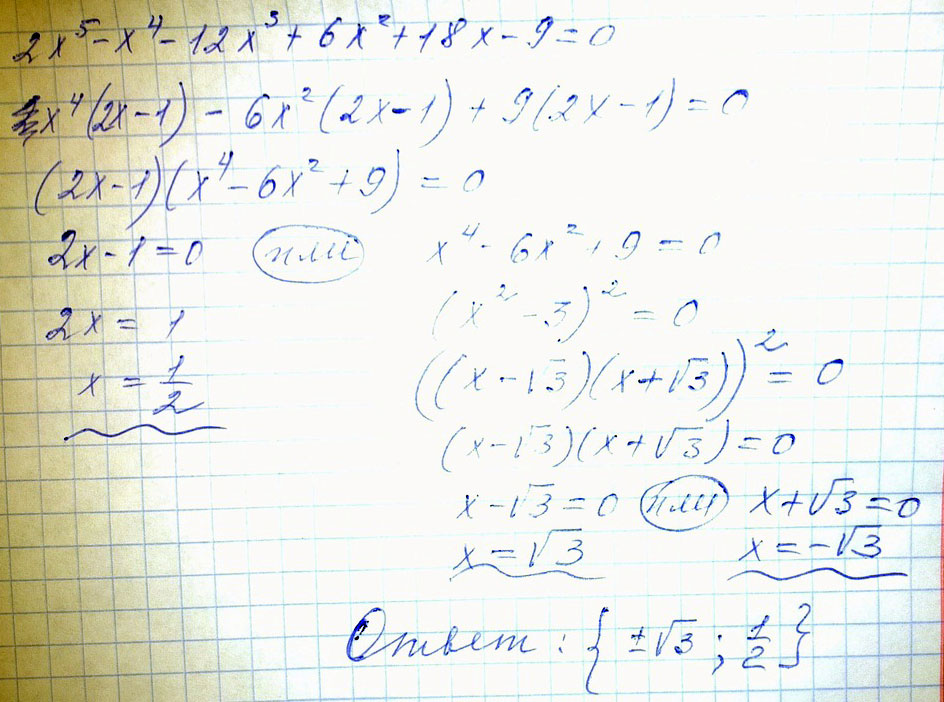
 Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...
Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...