дроби »
разложите на множители числитель и знаменатель дроби - страница 16
Решите уравнения методом разложения на множители.
x^2+4x-12=0
x^2-6x+8=0
x^2-16x+64=0
x^2-13x+42=0
Решение: X² + 4x - 12 = 0
x² + 4x = 12
x² = 12 или 4x = 12
x = \( \sqrt{12}\) x = 3
Ответ: \( \sqrt{12}\), 3
x² - 6x + 8 = 0
x² - 6x = -8
x² = -8 или -6x =-8
Корня нет x = 8 \\ 6 = 4 \\ 3 = 1 1 \\ 3
Ответ: 1 1 \\ 3
x² - 16x + 64 = 0
x² - 16x = - 64
x² = - 64 или -16x = - 64
Корня нет x = 4
Ответ: 4
x² - 13x + 42 = 0
x² - 13x = - 42
x² = - 42 или - 13x = - 42
Корня нет x = 42 \\ 13 = 3 3 \\ 13
Ответ: 3 3 \\ 13Решите уравнение, методом разложения на множители: x^4 - 2x^3 - 7x^2 - 4x + 4 =0
Решение: Если разложения на множители, то скорее всего нужно разлогать одночлены в сумму нескольких
x⁴-2x³-7x²-4x+4=0
(x⁴+2) -2x(x²+2) -7x²=0
(x⁴+4x²+4-4x²) - 2x(x²+2) - 7x² = 0
(x²+2)²-4x² -2x(x²+2) -7x² = 0
(x²+2)² - 2x(x²+2) -11x² =0 |:x
(x²+2)²÷x - 2(x²+2)÷x - 11 =0
Пусть (x²+2)/x = t, тогда получаем
t²-2t-11=0
$$ D=4+44=48 \\ t= \frac{2\pm4 \sqrt{3} }{2} =1\pm2 \sqrt{3} $$
Возвращаемся к замене
$$ \frac{x^2+2}{x} =1-2 \sqrt{3}|\times x \\ x^2+(-1+2 \sqrt{3})x+2=0 \\ D=(-1+2 \sqrt{3})-8=5-4 \sqrt{3} $$
D<0, значит уравнение корней не имеет
$$ \frac{x^2 +2}{x}=1+2 \sqrt{3} |\times x \\ x^2-(1+2 \sqrt{3} )x+2=0 \\ D=(1+2 \sqrt{3} )^2-8=5+4 \sqrt{3} \\ \\ x= \dfrac{1+2 \sqrt{3} \pm \sqrt{5+4 \sqrt{3} } }{2} $$
Решите уравнение с помощью разложения на множители.
а) (x-3)(2x+9)=0
б) 9y^2-1=0
в) t^2+6t+9=0
Решение: А) (x-3)(2x+9)=0
x-3=0 2x+9=0
x=3 2x=-9
x=-9/2
x= -4,5
Ответ: 3;-4,5
б) 9y²-1=0
(3y+1)(3y-1)=0
3y+1=0 3y-1=0
3y=-1 3y=1
y=-1\3 y=1\3
y=-⅓ y= ⅓
Ответ: ±⅓
в) t²+6t+9=0
(t+3)²=0
(t+3)(t+3)=0
t+3=0 t+3=0
t=-3 t=-3
Ответ: -3Решение уравнений с помощью разложения на множители.
Решите уравнения:
а) x^2 - 4 = 0
б) 4x^2 - 25 = 0
в) 5y^2 + 20у + 20 = 0
г) 2у^2 - 12у + 18 = 0
Решение: A) x^2-4=0
x^2=4
x=√4
x=2
б) 4x^2-25=0
4x^2=25
x^2=25/4
x^2=6.25
x=√6.25
x=2.5
в) 5y^2+20y+20=0
D1=100-5*20=0
y= -20/2*5
y=-2
г) 2y^2-12y+18=0
D1=36-2*18=
y= 12/2*2
y=3
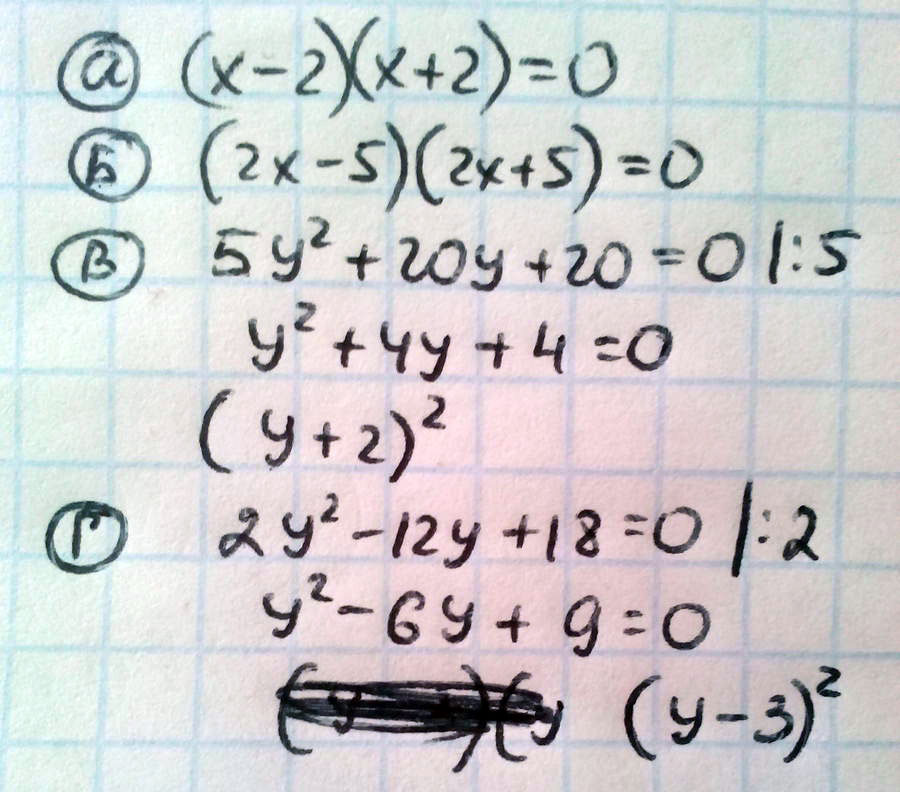
1) решите уравнение
а)x^3+9x^2+11x-21=0
б)4c^2(c-3)-20c(c-3)-25(3-c)=0
2) решите уравнение двумя способами
x^4-10x^3+35x^2-50x+24=0
3) применяя способы разложения на множители, найдите значение выражения:
(6^6*2^3-3^6)/(6^6+6^3*3^3+3^6)
Решение: 1) а) корнями многочлена являются делители свободного члена.
Проверим, делится ли левая часть на ( х +7)( +-7 - делители числа 21)
Делить будем "углом":
х³ +9х² + 11х -21 |(x +7)
x³ +7x² x² + 2x - 3
2x² + 11x
2x² + 14 x
-3x -21
-3x -21
х³ +9х² + 11х -21 = (x² +2x -3)(x +7) = (x + 3)(x - 1)(x + 7)
наше уравнение : (x + 3)(x - 1)(x + 7)=0⇒
⇒ х + 3 = 0 ⇒ х = -3; 1; -7
х - 1 = 0
х + 7 = 0
б) (с - 3)(4с² -20 с +25) = 0
(с - 3)((2с -5)² = 0
с - 3 =0 ⇒ с = 3
2с - 5 = 0 ⇒ с = 2,5
2) x^4 -10x^3 +35x^2 -50x +24=0
(x -4)(x^3 -6x^2 +11x -6) = 0
(x -4)(x -3)(x -2)(x -1) = 0
как это получилось? я многочлен разделил "углом" на (х -4)
получил в ответе х³ - 6х² +11х - 6. теперь этот результат надо разложить на множители:
(х³ - 6х² +11х) - 6 = х( х² -6х + 9 - 9 +11) -6=
=х((х-3)² +2) - 6= х(х-3)² + 2х -6=х(х-3)² + 2(х-3)=
=(х-3) ( х(х-3) +2) = (х-3)(х² -3х +2) = (х-3) (х-1)(х-2)
Теперь можно решать:
(x -4)(x -3)(x -2)(x -1) = 0
х = 4; 3; 2; 1
3) числитель = 6^6·2^3 - 3^6 = (2·3)^6·2^3 - 3^6=
= 2^6·3^6·2^3 - 3^6= 3^6(2^9 -1)= 3^6·(512 -1) = 3^6·511
знаменатель = 6^6 +6^3·3^3 + 3^6 =
=(2·3)^6 + (2·3)3·3^3 +3^6 = 2^6·3^6 + 2^3·3^3·3^3 + 3^6=
=2^6·3^6 +2^3·3^6 +3^6 = 3^6(2^6 +2^3 +1)= 3^6(64+8 +1) =
=3^6·73
Ответ:7


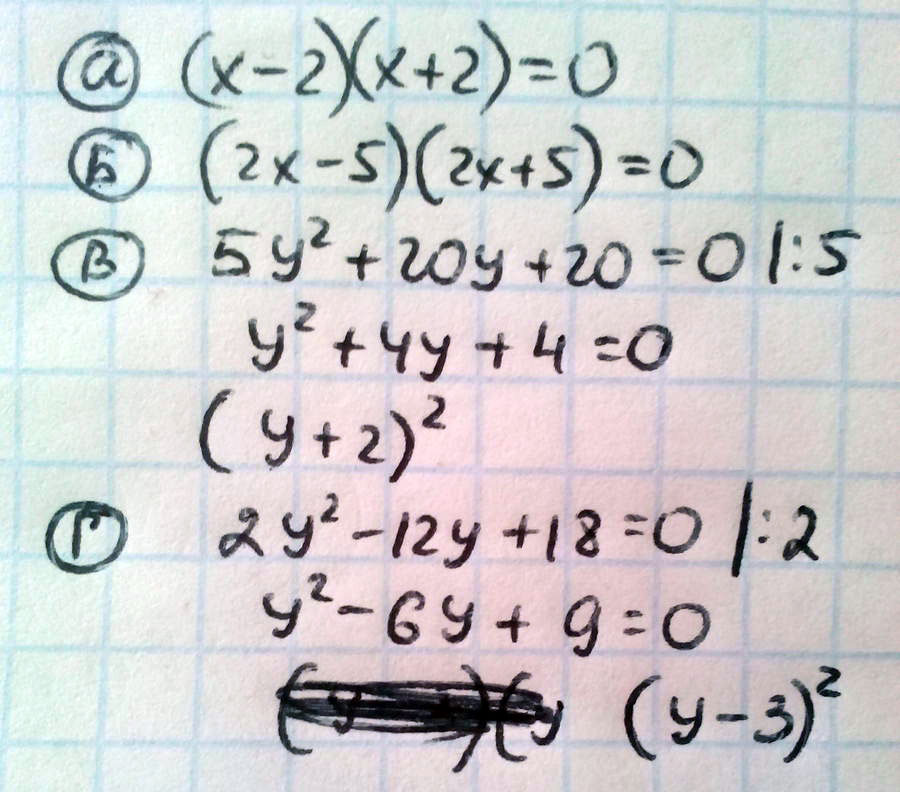

 Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...
Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...