дроби »

сократите дробь - страница 6

1. Вчислите:
$ a) \sqrt{121}-10\sqrt{6,4}*\sqrt{0,1} $
$ b) 2\sqrt{5}-\sqrt{45}+\sqrt{80} $
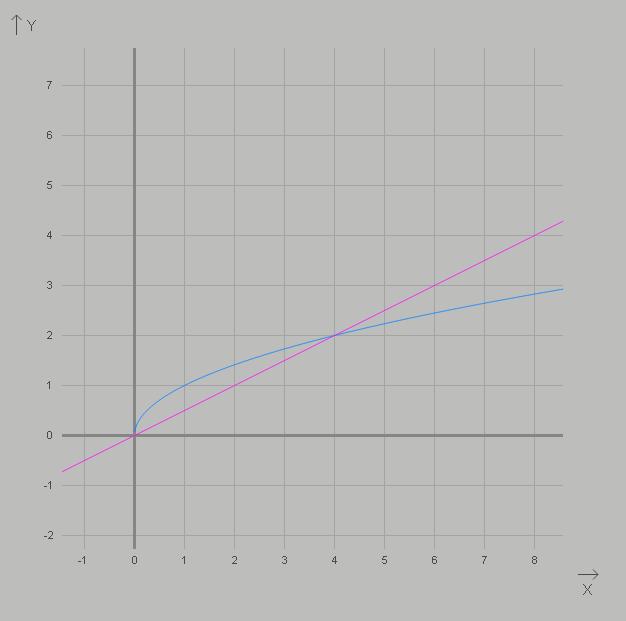
2. Постройте график функции $ y=\sqrt{x} $. Найдите:
а) наименьшее и наибольшее значения этой функции на отрезке [4;7];
б) координаты точки пересечения графика этой функции с прямой $ x-2y=0 $.
3. Сократите дробь: $ \frac{a-3\sqrt{a}}{a-9} $

Решение: $$ \sqrt{121}-10\sqrt{6,4}\cdot\sqrt{0,1}=11-10 \sqrt{6,4\cdot0.1} = \\\ =11-10 \sqrt{0.64} =11-10\cdot0.8=11-8=3 \\\\ 2\sqrt{5}-\sqrt{45}+\sqrt{80}= 2\sqrt{5}-\sqrt{5\cdot9}+\sqrt{5\cdot16}= \\\ =2\sqrt{5}-3\sqrt{5}+4\sqrt{5}=3\sqrt{5} \\ y=\sqrt{x};[4;7] \\\ y_{max}= \sqrt{7} \\\ y_{min}= 2 \\ x-2y=0 \\\ x=2y \\\ y= \frac{x}{2} \\\ \frac{x}{2} = \sqrt{x} \\\ x=2 \sqrt{x} \\\ x-2 \sqrt{x} =0 \\\ \sqrt{x} (\sqrt{x} -2)=0 \\\ \sqrt{x} =0 \\\ x_1=0 \\\ \sqrt{x} -2=0 \\\ \sqrt{x} =2 \\\ x_2=4 \\\ y_1=0 \\\ y_2=2 \\ (0,0) \\\ (4,2) \\ \cfrac{a-3\sqrt{a}}{a-9}=\cfrac{\sqrt{a}(\sqrt{a}-3)}{(\sqrt{a}-3)(\sqrt{a}+3)}=\cfrac{\sqrt{a}}{\sqrt{a}+3} $$

$sqrt - sqrt cdot sqrt - sqrt cdot . - sqrt . - cdot . - sqrt - sqrt sqrt sqrt - sqrt cdot sqrt cdot sqrt - sqrt sqrt sqrt y sqrt x y max sqrt y min x- y x y y frac x frac x s...$
№1
Данную дробь замените равную ей дробью, знаменатель которой равен 36:
1)1/2 2)2/6 3)5/9 4)1/12 5)7/18
№2
Запишите:
1) число 1 в виде дроби, знаменатель которой равен 32
2) число 8 в виде дроби, знаменатель которой равен 6
3) число 4 в виде дроби, знаменатель которой равен 12
№3
Пользуясь основным свойством дроби, найдите значение x, при котором верно равенство
1) x/5=4/20
2) 6/x=18/30
3)1/3=7/x
4)42/78=x/13
№4
Сократите дробь:
1)2/4
2)7/28
3)6/20
4)24/56
5)42/98
6)18/81
7)60/156
8)300/450

Решение: № 1. Данную дробь замените равную ей дробью, знаменатель которой равен 36:
1)1/2 = 18/36
2)2/6 = 12/36
3)5/9 = 20/36
4)1/12 = 3/36
5)7/18 = 14/36
№2
Запишите:
1) число 1 в виде дроби, знаменатель которой равен 32 = 32/32
2) число 8 в виде дроби, знаменатель которой равен 6 = 48/6
3) число 4 в виде дроби, знаменатель которой равен 12 = 24/12
№3
Пользуясь основным свойством дроби, найдите значение x, при котором верно равенство
1) x/5=4/20
20х = 5 * 4
20х = 20
х = 20 : 20
х = 1
2) 6/x=18/30
18х = 6 * 30
18х = 180
х = 180 : 18
х = 10
3)1/3=7/x
1х = 3 * 7
х = 21
4)42/78=x/13
78х = 13 * 42
78х = 546
х = 546 : 78
х = 7
№4
Сократите дробь:
1)2/4 = 1/2
2)7/28 = 1/4
3)6/20 = 3/10 = 0,3
4)24/56 = 3/7
5)42/98 = 6/14 = 3/7
6)18/81 = 2/9
7)60/156 = 5/13
8)300/450 = 6/9 = 2/3
№1. Сократите дроби. а) 17x^4y^2/34x^5y; b) 6b/bc-7b^2; c) p^2-g^2/6p-6g: №2. Запишите в виде дроби: а) 9/y+3 - 9y-7/y^2+3y; b) a-10/5a + 2a-1/a^2; c) 6x^2/x-y - 6x; d) 12n/mx : 48n/m^2; e) b+5/b^2-4 * 3b-6/b+5: №3. Сократите дроби и найдите ее значение: a) x^3-xy^3/xy^2+x^2y при х=1/3; у= 1/4. /- дробь. ^- это степень.

Решение: 1.
а)=у/2х
б)=6б/б(с-7б)=6/(с-7б)
с)=(р-ф)(р+ф)/6(р-ф)=(р+ф)/6
2.
а)=9/(у+3) -(9у-7)/у(у+3)=
=(9у-9у+7)/у(у+3)=7/у(у+3)
б)=(а(а-10)+5(2а-1))/5а^2=
=(а^2-10а+10а-5)/5а^2=
=(а^2-5)/5а^2
с)=(6х^2-6х(х-у))/(х-у)=
=(6х^2-6х^2+6ху)/(х-у)=
=6ху/(х-у)
д)=12н×м^2/мх×48н=м/4х
е)=(б+5)/(б-2)(б+2) ×3(б-2)/(б+5)=
=3/(б+2)
3.
=х(х^2-у^3)/ху(у+х)=
=(х^2-у^3)/у(у+х)
сократите дроби и запишите их виде десятичных дробей: 12/15, 21/35, 12/30, 45/50, 18/60, 56/80, 9/12, 21/60, 54/180, 102/24,135/60, 639/300. вычислите цепочку действий и найдите значение букв:1) a+5/8+1/4+1-2/5+1/5-3/10b

Решение: 12/15=4/5=0,8

21/35=3/5=0,6

12/30=4/10=0,4

45/50=9/10=0,9

18/60=3/10=0,3

56/80=7/10=0,7

9/12=3/4=0,75

21/60=7/20=35/100=0,35

54/180=6/20=30/100=0,3

102/24=51/12=17/4=425/100=4,25

135/60=27/12=9/4=225/100=2,25

639/300=213/100=2,13

1) a+5/8+1/4+1-2/5+1/5-3/10b =а+5/8+2/8-4/10+2/10-3/10 b =а+7/8+1-1/5-3/10b =а+28/40+40/40-8/40 -3/10b =а+60/40- 3/10b =а+1цел 1/2- 3/10b
Нужно сократить алгебраические дроби:
^ - степень. * - умножить. \ - дробная черта.
1) 36a^3b^2c-36a^3b^3\48ab^5-48ab^3c^2
2) (m-n)^2\m^2-n^2
3) 6pq-18p\(q-3)^2
4) c^2-18c+81\c-9
5) 5-2m\4m^2-20m+25
6) b^2-49\49-14b+b^2
7) 4n^2-4nm+m^2\4n^2-m^2
8) a^2-ab-b-c^2\b^2-a^2+2ac-c^2
9) x^2-yz+xz-y^2\x^2+yz-xz-y^2
10) 8^11-8^10-8^9\4^15-4^14-4^13
11) 87^3+43^3\87^2-87*43+43^2

Решение: 1) 36a^3b^2c-36a^3b^3\48ab^5-48ab^3c^2 = = 36a^3b^2(c - b) / 48ab^3(b^2-c^2) = 3a^2(c-b) /4(b-c)(b+c) =
= -3a^2/4b(b+c)
2) (m-n)^2\m^2-n^2 = (m-n)^2 / (m-n)(m+n) = (m-n)/(m+n)
3) 6pq-18p\(q-3)^2 = 6p(q - 3)/(q - 3)^2 = 6p/(q-3)
4) c^2-18c+81\c-9 = (c-9)^2 / (c-9) = c - 9
5) 5-2m\4m^2-20m+25 = (5 - 2m)/(5-2m)^2 = 1/(5-2m)
6) b^2-49\49-14b+b^2 = (b-7)(b+7)/(b-7)^2= (b+7)/(b-7)
7) 4n^2-4nm+m^2\4n^2-m^2 = (2n-m)^2 / (2n-m)(2n+m) =(2n-m)/(2n+m)
8) a^2-ab-bс-c^2\b^2-a^2+2ac-c^2 = [(a^2-c^2) - b(a+c)] / [b^2 - (a-c)^2] =
= [(a-c)(a+c) - b(a+c)] / [(b-(a-c)(b+(a-c)] = [(a+c)(a-c-b)]/ [-(a-c-b)(a+b-c)]=
= -(a+c)/(a+b-c)
9) x^2-yz+xz-y^2\x^2+yz-xz-y^2 = = [(x^2-y^2) - z(x-y)] / [(x^2-y^2) - z(x-y)]=1
10) 8^11-8^10-8^9\4^15-4^14-4^13 = 8^4(1-1^6-1^5) / 4^12(1^3-1^2-1) =
= 8^4 (1-1-1)/4^12(1-1-1) = 8^4/4^12
11) 87^3+43^3\87^2-87*43+43^2 =
= (87+43)(87^2-87*43+43^2)/(87^2-87*43+43^2) =(87+43) = 130

<< < 4 56 7 8 > >>