сократите дробь - страница 8
Сократите дроби
а) 15a
__________
3 + 21
_____
4a-6
Т. е числитель 15а разделить на знаменатель 3 плюс дробь 21/4а-6
б) 5b
____________
2- 4
____
3-2b
Т. е числитель 5b/ на знамен. 2 минус дробь 4/3-2b
в) 3x
__________
1- 6
______
10-5x
Т. е числитель 3х разделить на знаменатель 1 минус дробь 6/10-5х
г) 5y
________________
2- 7
_______
6+2y
Т. е числитель 5у разделить на знаменатель 2 минус дробь 7/6+2у
Решение: а) 15a 15а 15а * (4а-6) 60*а^2-90а
___________ ____________ ____________ ___________
3*(4а-6) + 21 = 12а -18 +21 = 12а + 3 = 12а+3___________ ____________
4a-6 4а-6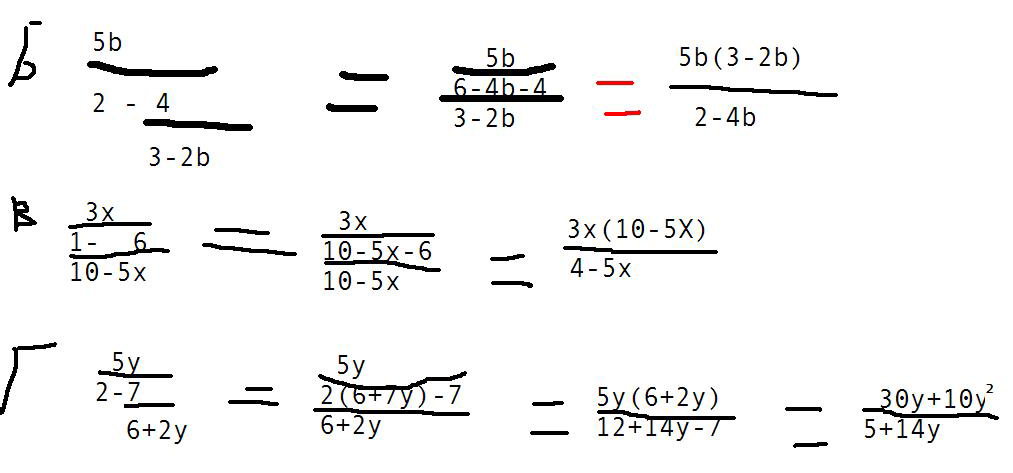
Сократите обыкновенные дроби.
1) 2/6; 3/9; 4/12; 5/25; 6/48; 10/90.
2) 6/14; 12/15; 18/21; 30/33; 24/27; 36/39.
Решение: 1) 1/3 2) 1/3 3) 1/3 4) 1/5 5) 1/8 6) 1/9
1)3/7 2) 4/5 3) 6/7 4) 10/11 5) 8/9 6) 12/132/6=1/3 (сокращаем на 2)
3/9=1/3 (сокращаем на 3)
4/12=1/3 (сокращаем на 4)
5/25=1/5 (сокращаем на 5)
6/48=1/8 (сокращаем на 6)
10/90=1/9 (сокращаем на 10)
____________________________
6/14=3/7 (сокращаем на 2)
12/15=4/5 (сокращаем на 3)
18/21=6/7 (сокращаем на 7)
30/33=10/11 (сокращаем на 3)
24/27=8/9 (сокращаем на 3)
36/39= 12/13 (сокращаем на 3)Сократите обыкновенные дроби
2:6; 3:9; 4:12; 5:25; 6:48; 10:90; 6:14; 10:22; 12:14; 14:16; 18:28; 20:26.
Решение: 2:6 сокращаем 1:3
3:9 сокращаем 1:3
4:12 сокращаем 1:3
5:25 сокращаем 1:5
6:48 сокращаем 1:8
10:90 сокращаем 1:9
6:14 сокращаем 3:7
10:22 сокращаем 5:11
12:14 сокращаем 6:7
14:16 сокращаем 7:8
18:28 сокращаем 9:14
20:26 сокращаем 10:13$$ \frac{2}{6} = \frac{1}{3}. \frac{3}{9} = \frac{1}{3}. \frac{4}{12} = \frac{1}{3}. \frac{5}{25} = \frac{1}{5}. \frac{6}{48} = \frac{1}{8}. \frac{10}{90} = \frac{1}{9}. \frac{6}{14} = \frac{3}{7}. \frac{10}{22} = \frac{5}{11}. \frac{12}{14} = \frac{6}{7}. \\ \frac{14}{16} = \frac{7}{8}. \frac{18}{28} = \frac{9}{14}. \frac{20}{26} = \frac{10}{13} $$
Приведите обыкновенные дроби 1__3; 2__3; 1__5; 2__5; 4__5; 1__6; 5__6; 3__10; 7__10; 9__10; обыкновенной дроби со знаменателем 30.
Сократите обыкновенны дроби. 6__9; 12__15; 18__21; 30__33; 24__27; 36__39.
Например: 2-6=1-3;
1)2*___5 2) 2*___7 3)3*___5 4)4*___3 5)10*___3
3*___6 9*___4 20*___2 9*___7 23*___10
6) 10*___2 7)4*___5 8) 8*___9
21*__30 15*__16 27*___16
Решение: 5.4.2. Примеры сокращения обыкновенных дробейДеление и числителя и знаменателя дроби на их общий делитель, отличный от единицы, называют сокращением дроби. Чтобы сократить обыкновенную дробь, нужно разделить ее числитель и знаменатель на одно и то же натуральное число. Это число является наибольшим общим делителем числителя и знаменателя данной дроби. Возможны следующие формы записи решенияпримеров на сокращение обыкновенных дробей. Учащийся вправе выбрать любую форму записи. Примеры. Упростить дроби. Сократим дробь на 3 (делим числитель на 3; делим знаменатель на 3). Сокращаем дробь на 7. Выполняем указанные действия в числителе и знаменателе дроби. Полученную дробь сокращаем на 5. Сократим данную дробь 4) на 5·7³ — наибольший общий делитель (НОД) числителя и знаменателя, который состоит из общих множителей числителя и знаменателя, взятых в степени с наименьшим показателем. Разложим числитель и знаменатель этой дроби на простые множители. Получаем: 756=2²·3³·7 и 1176=2³·3·7². Определяем НОД (наибольший общий делитель) числителя и знаменателя дроби 5). Это произведение общих множителей, взятых с наименьшими показателями. НОД(756; 1176)=2²·3·7. Делим числитель и знаменатель данной дроби на их НОД, т. е. на 2²·3·7получаем несократимую дробь 9/14. А можно было записать разложения числителя и знаменателя в виде произведения простых множителей, не применяя понятие степени, а затем произвести сокращение дроби, зачеркивая одинаковые множители в числителе и знаменателе. Когда одинаковых множителей не останется — перемножаем оставшиеся множители отдельно в числителе и отдельно в знаменателе и выписываем получившуюся дробь 9/14. И, наконец, можно было сокращать данную дробь 5) постепенно, применяя признаки деления чисел и к числителю и к знаменателю дроби. Рассуждаем так: числа 756 и 1176 оканчиваются четной цифрой, значит, оба делятся на 2. Сокращаем дробь на 2. Числитель и знаменатель новой дроби — числа 378и 588 также делятся на 2. Сокращаем дробь на 2. Замечаем, что число 294 — четное, а189 — нечетное, и сокращение на 2 уже невозможно. Проверим признак делимости чисел189 и 294 на 3.(1+8+9)=18 делится на 3 и (2+9+4)=15 делится на 3, следовательно, и сами числа 189 и294 делятся на 3. Сокращаем дробь на 3. Далее, 63 делится на 3, а 98 — нет. Перебираем другие простые множители. Оба числа делятся на 7. Сокращаем дробь на 7 и получаем несократимую дробь 9/14.Сократите, если это возможно, обыкновенные дроби: 1) 32/46; 2) 10/80; 3) 135/315; 4) 142/208; 5) 225/425; 6) 21/49; 7) 41/282; 8) 45/702; 9) 23/32; 10) 36/54.
Решение: 1) 32/46 = 16/23
2) 10/80 = 1/8
3) 135/315 = 3/7
4) 142/208 = 71/104
5) 225/425 = 9/17
6) 21/49 = 3/7
7) 41/282
8) 45/702 = 5/78
9) 23/32
10) 36/54 = 2/31)
32/46=16/23 (сокращаем на 2)
2)10/80=1/8 (сокращаем на 10)
3) 135/315 =3/7 (сокращаем на 45)
4) 142/208 = 71/104 (сокращаем на 2)
5) 225/425=9/17 (сокращаем на 25)
6) 21/49 =3/7 (сокращаем на 7)
7) 41/282 нельзя сократить
8)45/702=5/78 (сокращаем на 9)
9) 23/32 не сокращается
10) 36/54 = 2/3 (сокращаем на 18)

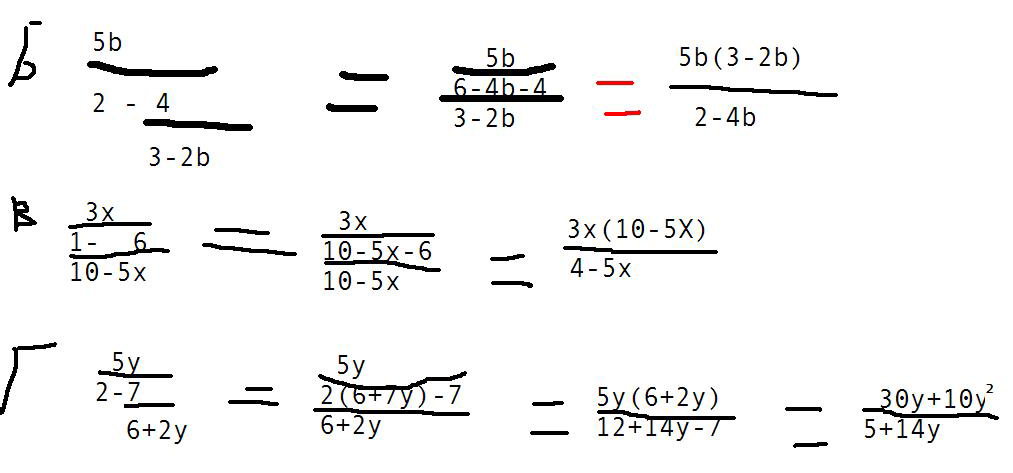
 Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...
Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...