примеры с дробями - страница 10
Пользуясь основным свойством дроби, найдите значение х, при котором верно равенство х/5=4/20, 6/×=18/30, 1/3=7/×, 42/78=×/13
Решение: $$ \frac{x}{5} = \frac{4}{20} \\ \frac{x}{5} = \frac{1}{5} $$
x = 1
$$ \frac{6}{x} = \frac{18}{30} \\ \frac{6}{x} = \frac{6}{10} $$
x = 10
$$ \frac{1}{3} = \frac{7}{x} \\ \frac{7}{21} = \frac{7}{x} $$
x = 21
$$ \frac{42}{78} = \frac{x}{13} \\ \frac{7}{13} = \frac{x}{13} $$
x = 7X/5=4/20
x/5=1/5, т. е. х=1
6/x=18/30
6/x=3/5, т. е. х=10
1/3=7/x, т. е. х=7*3=21
42/78=x/13, т. е. х = 7
Делаем это все путем сокращения дробей и подбирания частейПользуясь основным свойством дроби найдите значение а, при котором верно равенство 1) а/6=9/54 2)7/а=49/28 3)27\45=3/а а/32=5/8.
Решение: Если и числитель и знаменатель дроби умножить или разделить на одно и то же число, то значение дроби не изменится.
а/6 = 9/54
54 : 6 = 9 - доп. множитель
а = 9 : 9
а = 1
1/6 = 9/54
7/а = 49/28
49 : 7 = 7 - доп. множитель
а = 28 : 7
а = 4
7/4 = 49/28
27/45 = 3/а
27 : 3 = 9 - доп. множитель
а = 45 : 9
а = 5
27/45 = 3/5
а/32 = 5/8
32 : 8 = 4 - доп. множитель
а = 5 * 4
а = 20
20/32 = 5/8
Напишите неверные неравенства
1) 5/7=35/49
2)14/24=2/3
3)7/9=42/54
4)4/5=32
НОМЕР №2
Данную дробь замените разной ей дробью, знаменатель которой равен 48:
1) 1/3
2)5/6
3)4/8
4)1/16
5)5/24
НОМЕР №3
Пользуясь основным свойством дроби, найдите значение а, при котором верно равенство:
1)a/8=15/40
2)9/a=36/52
3)1/8=5/a
4)21/98=a/14
РЕБЯТА
Решение: № 1. Неверные неравенства:2) 14/24 = 2/3 - неверно, так как 14/24 = 7/12
4) 4/5 = 32 - неверно, так как 4/5 - дробь, а 32 - целое число
№ 2. Привести дроби к знаменателю 48:
1) 1/3 = 16/48 (48 : 3 = 16 - доп. множитель для 1/3)
2) 5/6 = 40/48 (48 : 6 = 8 - доп. множитель для 5/6)
3) 4/8 = 24/48 (48 : 8 = 6 - доп. множитель для 4/8)
4) 1/16 = 3/48 (48 : 16 = 3 - доп. множитель для 1/16)
5) 5/24 = 10/48 (48 : 24 = 2 - доп. множитель для 5/24)
№ 3. Найти значение а:
1) а/8 = 15/40, а = 3 (40:8=5; 15:5=3)
2) 9/а = 36/52, а = 13 (36:9=4; 52:4=13)
3) 1/8 = 5/а, а = 40 (5:1=5; 8*5=40)
4) 21/98 = а/14, а = 3 (98:14=7; 21:7=3)
Найдите значение х, при котором значение дроби х/3-х меньше значения дроби 6/х на 1
Решение: Составим уравнение6/х-х/3-х=1
Приведем к общему знаменателю
(6*(3-х)-х*х)/х*(3-х)=1
Раскроем скобки
18-6х-х²/3х-х²=1
18-6х-х²=3х-х²
18-6х-х²-3х+х²=0
-9х+18=0
-9х=-18
х=2
Ответ: х=2
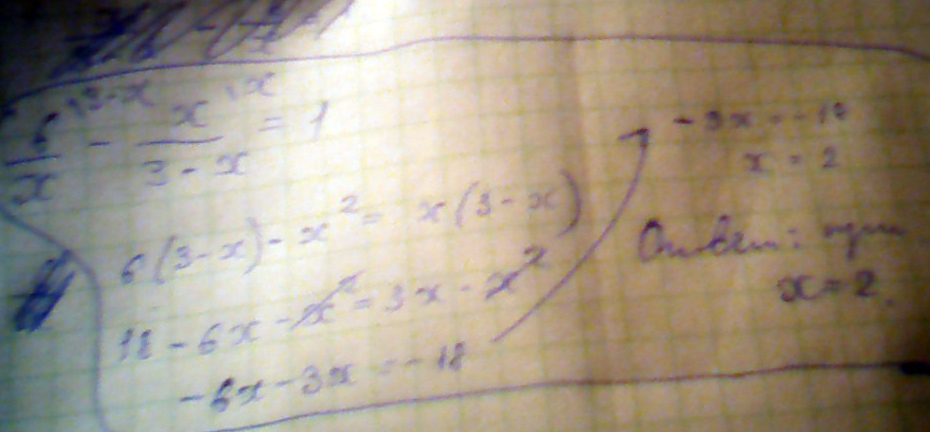
найдите значение а, при котором значение дроби равно нуль:
1) 9-3а
9+3а
2) 7+3а
7-3а
Решение: Дробь равна 0, когда числитель РАВЕН 0, а ЗНАМЕНАТЕЛЬ НЕ РАВЕН 0
1). 9-3а
9+3а
Числитель
9-3а=0
-3а=9
а=-3, единственный корень (И ТОТ НЕ ТОТ)
но тогда ЗНАМЕНАТЕЛЬ 9+3а=9+3*(-3)=9-9=0, а НА НОЛЬ ДЕЛИТЬ НЕЛЬЗЯ
Ответ НЕТ решения
2) 7+3а
7-3а
Числитель
7+3а=0
а=-7/3
Знаменатель
7-3а=7-3*(-7/3)=7+7=14
Ответ: -7/3=-2 1/3

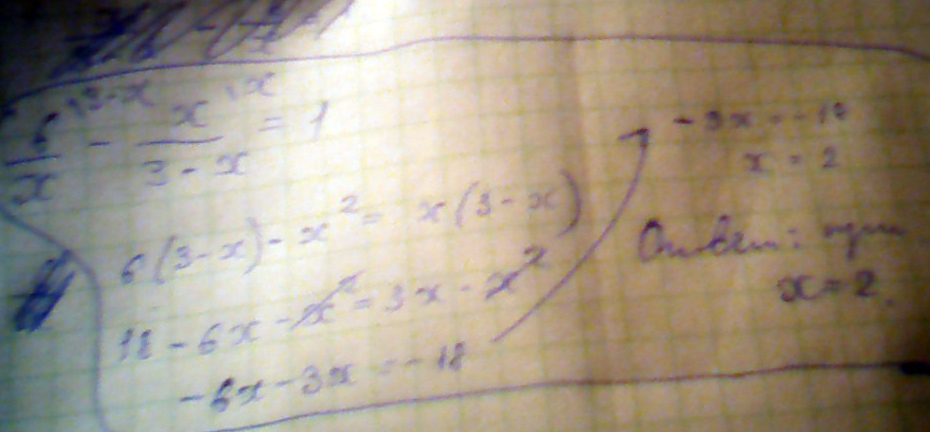
 Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...
Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...