дроби »
примеры с дробями - страница 8
Нужно 20 примеров на деление, умножение, сложение и вычитания на десятичные дроби.
Решение: Сложение десятичных дробей:
1) 0,5 + 0,2 = 0,7
2) 0,07 + 0,03 = 0,1
3) 0,08 + 0,2 = 0,28
4) 0,1 + 0,9 = 1
5) 0,012 + 0,25 = 0,262
Вычитание десятичных дробей:
1) 0,5 - 0,2 = 0,3
2) 0,07 - 0,03 = 0,04
3) 0,08 - 0,2 = -0,12
4) 0,1 - 0,1 = 0
5) 0,012 - 0,25 = -0,238
Умножение десятичных дробей:
1) 0,5 * 0,2 = 0,1
2) 0,07 * 0,03 = 0,0021
3) 0,08 * 0,2 = 0,016
4) 0,5 * 0,1 = 0,05
5) 0,012 * 0,25 = 0,003
Деление десятичных дробей:
1) 0,5 : 0,2 = 2,5
2) 0,25 : 0,5 = 0,5
3) 0,1 : 0,1 = 1
4) 0,081 : 0,36 = 0,225
5) 0,1 : 0,5 = 0,2Разложите данные дроби в десятичные с помощью деления уголком: а)7/5 3/16 48/15 г)7/4 3/2 9/5 ;)625/125 860/400 33/60
Решение: Я приложу рисунок с делением уголком для примеров 7/5 и 3/16, остальные делаются точно также.
7/5 = 1,4
Объясняю подробно, как делить уголком.
7 делим на 5, получаем в частном 1. Умножаем 1 на 5, получаем 5.
Пишем 5 под 7 и вычитаем, получаем 2. 2 меньше 5, поэтому в частном ставим запятую, а к 2 приписываем 0, получаем 20.
Делим 20 на 5, получаем 4. Умножаем 4 на 5, получаем 20.
Пишем 20 под 20, вычитаем, получаем 0. Деление окончено.
3/16 = 0,1875
Тут сразу 3 меньше 16, поэтому к 3 приписываем 0, а в частном тоже ставим 0 и запятую. Далее все точно также, как в 1 примере.
Другие примеры:
48/15 = 16/5 = 3,2
7/4 = 1,75
3/2 = 1,5
9/5 = 1,8
625/125 = 5
860/400 = 43/20 = 2,15
33/60 = 11/20 =0,55
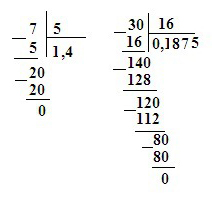
Деление десятичной дроби на десятичную дробь 18,4:7,36
Решение: При делении десятичной дроби на десятичную дробь, надо делитель перевести в целое число:
7,36*100=736
также теперь делимое надо умножить на 100(на какое число умножается делитель, на такое же умножается делимое):
18,4*100=1840
теперь надо просто
1840:736
1840 _| 736
-1472 _|-
-_| 2,5
_3680
- 3680
-
____0
Ответ: 2,5Умножение и деление десятичной дроби на 10 100 и тд в какую сторану ставится запитая при умножение и деление
Решение: Умножение
При умножении на 10 запятая переносится на один знак вправо, например:
0,565*10=5,65; 2,346*10=23,46; 0,046*10=0,46
При умножении на 100 запятая переносится на 2 знака вправо, например:
0,000456*100=0,0456; 3,148*100=314,8
Деление
При делении на 10 запятая переносится на один знак влево, например:
0,65:10=0,065; 2,957:10=0,2957; 32,55:10=3,255
При делении на 100 запятая переносится на два знака влево, например:
45,78:100=0,4578; 0,34:100=0,0034(если не хватает знаков добавляется слева соответствующее количество нулей); 0,023:100=0,00023; 456,87:100=4,5687, и так далееКак понять где ставить запятую при делении десятичной дроби на число? например:4.14:0.3? , а то завтра контрольная, а я до сих пор не поняла где ставить запятую(((
Решение: Смотрите у вас даны два числа, в данном случае десятичные числа 4.14 и 0.3, мы для упрощения задачи переносим запятую в делителе, то есть в числе 0.3 и получиться 3, но так как мы перенесли запятую во втором числе, то должны и в первом на столько же, получится 41.4:3 =13.8, а значит переносим на одну. как-то так

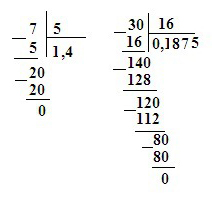
 Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...
Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...