дроби »
примеры с дробями - страница 12
Найдите значение функции
f(x) = √x÷(5-X) корень относится ко всей дроби
Решение: $$ f(x)=\sqrt{ \frac{x}{5-x} } \\ \frac{x}{5-x} \geq 0 ; x=5, x=0. $$
область определения функции x∈[0;5)
область значений функции:
$$ y’ = \frac{5}{2 \sqrt{x} \sqrt{( 5-x)^{3} } } ; x=0; x=5 $$
y’>0 при х∈(0;5) => функция возрастает на всей области определения
y(0) = 0
$$ \lim_{x \to {5-e}} \sqrt{ \frac{x}{5-x} } = \sqrt{ \frac{5-e}{e} } = \sqrt{ \frac{5}{e}-1 } = inf $$
y(x)∈[0;∞) - область значений функции1. Найдите сумму всех натуральных значений n, при которых значение дроби тоже будет натуральным числом n^2-24/n; (n²-12):n
Решение: n^2-24/nнатуральное число, если
n > 24/n,
24/n - натуральное число
n^2 > 24,
n = {1,2,3,4,6,8,12,24}
n = {6,8,12,24}
сумма = 50n^2-12/n
(n^2-12)/n=n-12/n
натуральное число, если
n > 12/n,
12/n - натуральное число
n^2 > 12,
n = {1,2,3,4,6,12,}
n = (4,6,12}
сумма = 222) (n²-12):n=n-12/n, чтобы эта разность была натуральным числом, необходимо, чтобы n>12/n и 12/n тоже было натуральным числом.
Делители числа 12, это 1, 2, 3, 4, 6, 12. Из них только 4, 6 и 12 удовлетворяют этим двум условиям. Их сумма 4+6+12=22
1) Рассуждаем аналогично.
1) Найдите сумму всех натуральных значений n при которых значение дроби ( n*(2) - 24)/n тоже будет натуральным числом.
2) Решить уравнение: ctg(п/2 - 3х) = tg2x+ tgx
Решение: 1)
(n^2 - 24)/n = n - 24/n
натуральное число, если
n > 24/n,
24/n - натуральное число
n^2 > 24,
n = {1,2,3,4,6,8,12,24}
n = {6,8,12,24}
сумма = 50
2)
$$ ctg(\pi/2 - 3x) = tg(2x)+ tg(x) \\ tg(3x) = tg(2x)+ tg(x) \\ ОДЗ x = (1/6, 1/4, 1/2, 3/4, 5/6)\pi + \pi \cdot n \\ tg(x+2x) = tg(2x)+ tg(x) \\ \frac{tg(x) + tg(2x)}{1-tg(x)tg(2x)} = tg(x) + tg(2x) $$
совокупность:
$$\left[\begin{array}{l} tg(x) + tg(2x) = 0, \\ 1 - tg(x)tg(2x) = 1 \end{array}\right. \\ \left[\begin{array}{l} tg(x) + \frac{2 tg(x)}{1 - tg^2(x)} = 0, \\ tg(x)tg(2x) = 0 \end{array}\right. \\ \left[\begin{array}{l} tg(x) = 0, \\ tg(2x) = 0, \\ 1 + \frac{2}{1 - tg^2(x)} = 0 \end{array}\right. \\ \left[\begin{array}{l} x = \pi \cdot n, \\ x = \frac{\pi}{2} \cdot n, \\ tg(x) = \pm \sqrt{3} \end{array}\right. \\ \left[\begin{array}{l} x = \frac{\pi}{2} \cdot n, \\ x = \pm \frac{\pi}{6} + \pi \cdot n \end{array}\right. $$
исключаем корни, не принадлежащие ОДЗ
$$ x = \pi \cdot n $$Значение дроби, сумма числителя и знаменателя которой равна 65, равно дроби 6/7. Найдите эту дробь.
Решение: Х числитель
65-х знаменатель
х/(65-х)=6/7
7х=390-6х
13х=390
х=30 числитель
65-30=35 знаменатель
дробь 30/35=6/7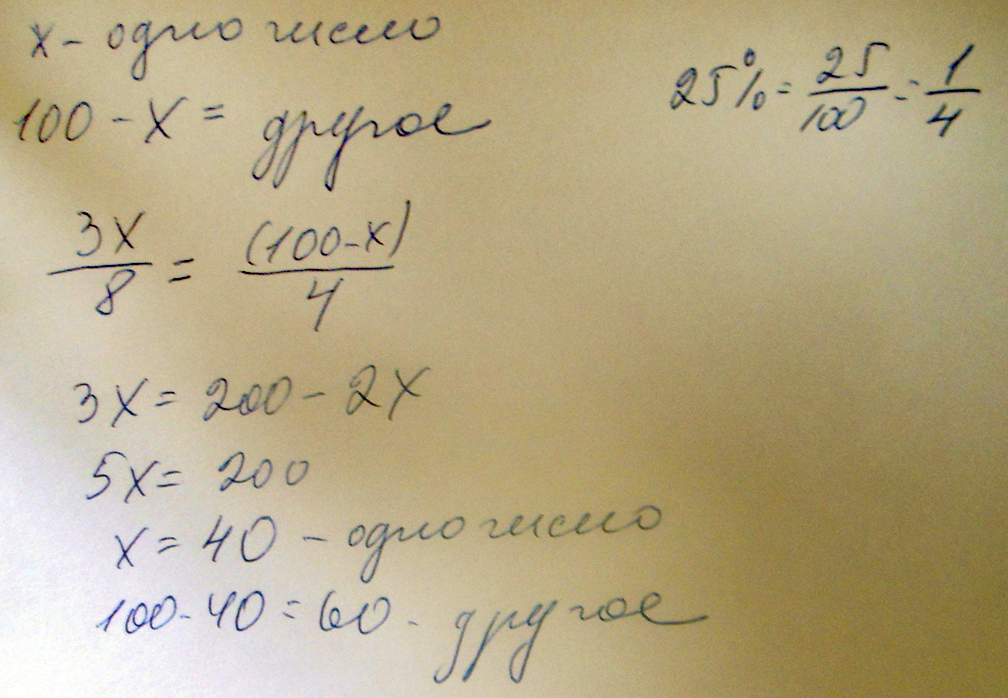
После сокращения дроби 21/а на 3 получилась дробь b/4. Найдите значение a и b
Решение: 21/а сокращаем на 3 получается 7/а, условие говорит что после сокращения на 3 получилась дробь в/4, из этого следует:
что а=4, в=7

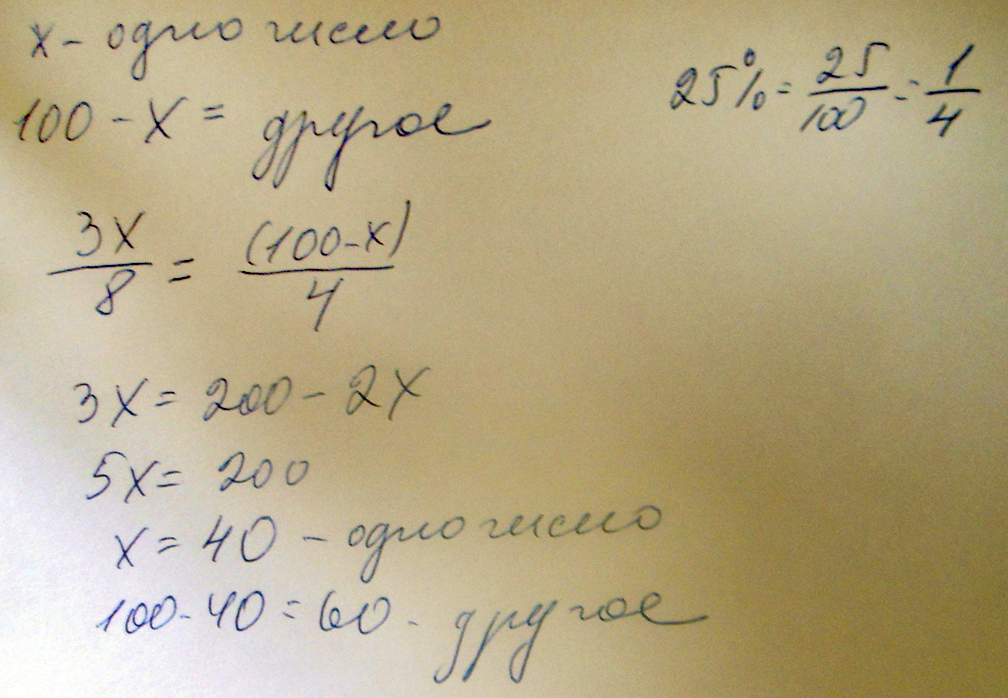

 Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...
Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...