дроби »
примеры с дробями - страница 14
Вычислите две 9-тых это дробь умножить на (-5) это под а)
Б) - 12 15-тых тоже дробь : на (-6)
В) -3 4-тых дробь умножить на 2
Г) -7 15-тых это дробь : на (-3)
Решение: А) -10/9 = - 1.1/9
б) 72/15 = 4.12/15 = 4.4/5
в) - 6/4 = - 1.1/2
г) 21/15 = 7/5 = 1.2/5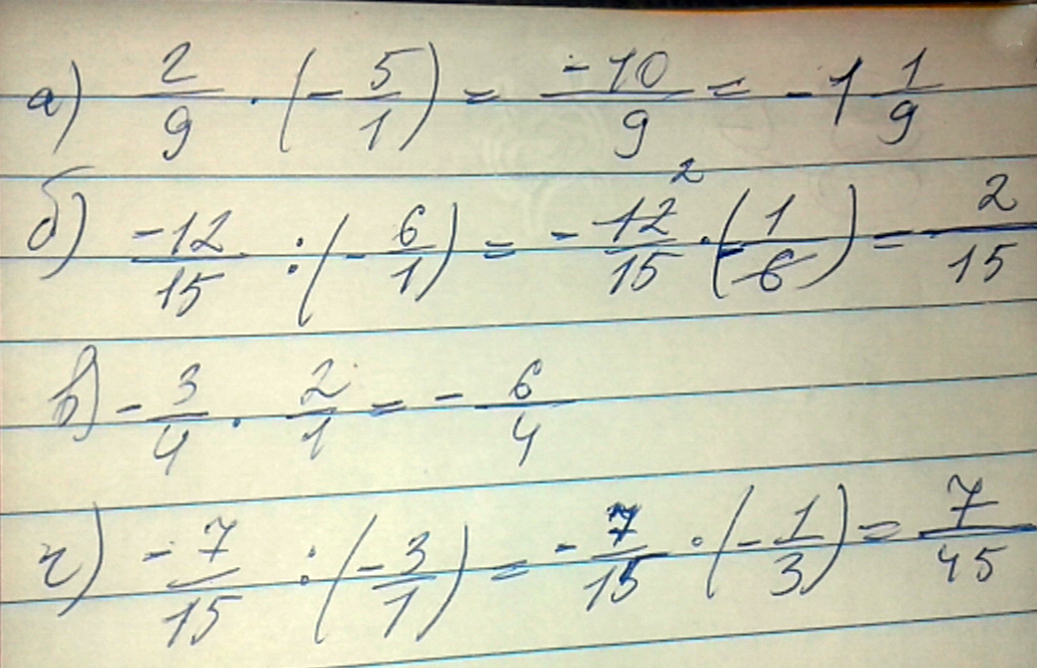
1 целая 3 восьмых(это дробь) умножить на 1 целую две седьмых эм(м) и умножить на две третих(дробь) эм(м)
Решение: 1 3/8 * 1 2/7 * 2/3 = 11/8 * 9/7 * 2/3 = 11/4 * 3/7 = 33/28 = 1 5/28
Целые части мы возводим в дробь, затем сокращаем 8 из знаменателя первой дроби с 2 из числителя третьей и 9 из числителя второй дроби с 3 из знаменателя третьей. Третья дробь автоматически исчезает, т. к. она превращается в 1/1 и у нас остается 11/4 * 3*7. Тут уже ничего сократить нельзя, поэтому мы перемножаем числитель с числителем, знаменатель со знаменателем. 11* 3 = 33 и 4 * 7 = 28. Получается 33/28, выделяем целую часть = 1 5/28Выберите верные утверждения.1) при умножении двух нецелых чисел всегда получается невелик число.2) если к числителю и знаменателю любой дроби прибавить 3, то дробь не изменится.3) если числитель и знаменатель данной дроби поменять местами, а затем полученную дробь умножить на данную, то произведение будет равно 1. 4) если числитель положительной дроби увеличить в 5 раз, то дробь увеличится в 5 раз. в ответе укажите номера верных утверждений без пробелов, запятых и других дополнительных символов.
Решение: 1) при умножении двух нецелых чисел всегда получается невелик число === нет 3,5+1,5=5
2) если к числителю и знаменателю любой дроби прибавить3, то дробь не изменится.===нет 1/2≠4/5
3) если числитель и знаменатель данной дроби поменять местами, а затем полученную дробь умножить на данную, то произведение будет равно 1.===да 3/4*4/3=1
4) если числитель положительной дроби увеличить в 5 раз, то дробь увеличится в 5 раз.===да 1/2=0,5. 1/2*5=2,53 умножить на дробь (все под корнем) корень из 8 + 2 корня из семи, разделить на знаменатель (все под корнем) из 8 - 2 корня из 7. вычесть из этого дробь (все под корнем) из 3 + корень из 7, в знаменателе (все под корнем) 3 - корень из 7. И умножить последнюю дробь на 2.
Решение: $$ 3\cdot \frac{ \sqrt{8+2 \sqrt{7} } }{ \sqrt{8-2 \sqrt{7} } }-2\cdot \frac{ \sqrt{3+ \sqrt{7} } }{ \sqrt{3-\sqrt{7} } }= $$
избавляемся от иррациональностей в знаменателях.
Умножаем и числитель и знаменатель на такое же выражение, которое написано в числителе каждой дроби.
$$ 3\cdot \frac{ \sqrt{(8+2 \sqrt{7})^2}}{ \sqrt{8^2-(2 \sqrt{7})^2 } }-2\cdot \frac{ \sqrt{(3+ \sqrt{7})^2 } }{ \sqrt{(3)^2-(\sqrt{7})^2 } }=3\cdot \frac{8+2 \sqrt{7} }{6}-2\cdot \frac{3+ \sqrt{7} }{ \sqrt{2} }= \\ = \frac{8+2 \sqrt{7} }{2}-2\cdot \frac{(3+ \sqrt{7}) \sqrt{2} }{ 2 } = \frac{8+2 \sqrt{7}-6 \sqrt{2} -2 \sqrt{14} }{2}=4+ \sqrt{7}-3 \sqrt{2}- \sqrt{14} $$8 дробь 3 умножить на корень 1целая 7 дробь 20 умножить на корень 15 дробь 16
Решение: Ответ:3
1) Выражения под корнями нужно перемножить. Перед этим смешанное число под первым выражением переводим в неправильную дробь 27/20.
В итоге по корнем перемножаем дроби 27/20 и 15/16. И получаем под корнем 405/320.
2)405/320 сокращаем на 5. Получается под корнем 81/64. Из чисел 81 и 64 можно извлечь корень. После извлечения получаем дробь 9/8.
3) В конце умножаем 8/3 на 9/8. Сокращаем. И получаем ответ:3

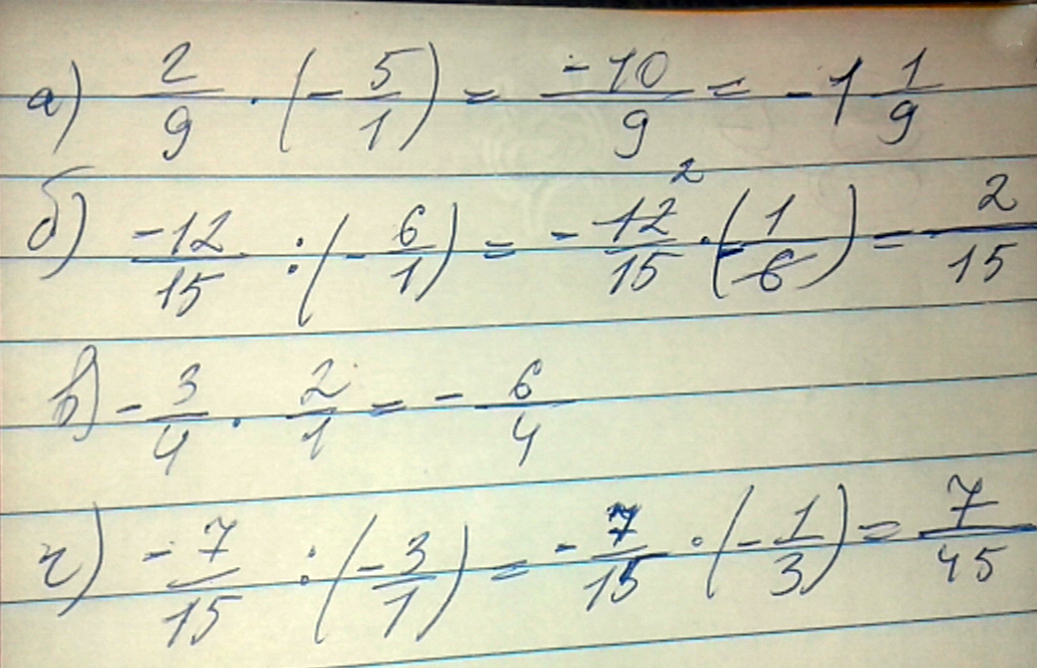
 Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...
Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...