примеры с дробями - страница 16
1)3 корень из 27 умножить на 81 в степени 3 четвёртых умножить на одну вторую в степени две третьих умножить на корень третьей степени из 4
2)10 в степени одна четвёртая умножить на 10 в степени одна четвёртая умножить на 5 в степени одна вторая
3) в числителе корень третьей степени из 375 умножить на корень третьей степени из 27
в знаменателе корень третьей степени из 81
4) в числителе х-у, в знаменателе х в степени одна вторая- у в степени одна вторая минус в числителе у в степени одна вторая+ у, в знаменателе у в степени одна вторая и найти значение при х=16, у=25
5) в скобках дробь: в числителе корень из а+корень из х, в знаменателе корень из а+х минус дробь: в числителе корень из а+х, в знаменателе корень из а+корень из х скобка закрылась разделить на дробь: в числителе 1, в знаменателе в скобках корень из а+ корень из х скобка закрылась умножить на корень из а+х
Решение: 1) $$ 3 \sqrt{27}*81^{ \frac{3}{4} }* (\frac{1}{2} )^{ \frac{2}{3} }* \sqrt[3]{4}= \\ =9 \sqrt{3}* \sqrt[4]{(3^{3}) ^{4} }* \frac{1}{ \sqrt[3]{2^{2} } }* \sqrt[3]{4}=9 \sqrt{3} *3^{3}=243 \sqrt{3} $$
2) $$ 10^{ \frac{1}{4} } *10^{ \frac{1}{4} }*5^{ \frac{1}{2} }=10^{ \frac{1}{2} }*5^{ \frac{1}{2} }= \sqrt{10} * \sqrt{5}= \sqrt{50}=5 \sqrt{2} $$
3) $$ \frac{ \sqrt[3]{375}* \sqrt[3]{27} }{ \sqrt[3]{81} } = \frac{ \sqrt[3]{3*125}*3 }{3 \sqrt[3]{3} } = \sqrt[3]{125}=5 $$
4) $$ \frac{x-y}{ \sqrt{x} - \sqrt{y} } - \frac{ \sqrt{y}+y }{ \sqrt{y} }= \\ = \frac{ (\sqrt{x} + \sqrt{y})( \sqrt{x} - \sqrt{y})}{\sqrt{x} - \sqrt{y}} -1- \sqrt{y} = \\ = \sqrt{x} + \sqrt{y} -1- \sqrt{y} = \sqrt{x} -1= \sqrt{16}-1=3 $$
5) $$ ( \frac{ \sqrt{a}+ \sqrt{x}}{ \sqrt{a+x}}- \frac{ \sqrt{a+x} }{ \sqrt{a}+ \sqrt{x} }): \frac{1}{(\sqrt{a}+ \sqrt{x}) \sqrt{a+x}}= \\ = \frac{ (\sqrt{a}+ \sqrt{x})^{2}-a-x }{ \sqrt{a+x}( \sqrt{a}+ \sqrt{x})}*(\sqrt{a}+ \sqrt{x})\sqrt{a+x}= \\ =a+2 \sqrt{ax} +x-a-x=2 \sqrt{ax} $$Нужно составить уравнение и решить его:
а) Если из (дробь) 3/4 неизвестного числа вычесть 10 и полученную разность умножить на 2, то получится 100;
б) Если к неизвестному числу прибавить столько же да ещё (дробь) 10 целых 1/3, то получится (дробь) 95 целых 2/5
Решение: а) (3/4*х-10)*2=100 б) х+х+10 целых 1/3=95 целых 2/53/4*х-10=100 : 2 2х= 95 целых 2/5- 10 целых 1/3
3/4*х-10= 50 2х=85 целых 1/15
3/4*х=50+10 х= 85 целых 1/15 : 2
3/4*х=60 х=42 целых 8/15
х=60 : (3/4)
х= 80
Выполнить действия 2а+10 черта дроби 3в-9 умножить 4b-12 черта дроби а+5
Решение: 2(а+5) черта дроби 3(в-3) умножить 4(в-3) черта дроби а+5 теперь всё, что с числами сокращается и остаётся 8/32а+10 черта дроби 3в-9 умножить 4в-12 черта дроби а+5 = 2(а+5) черта дроби 3(в-3) умножить 4(в-3) черта дроби а+5 = сокращаем а+5 и а+5 и в-3 и в-3 = 8 черта дроби 3.
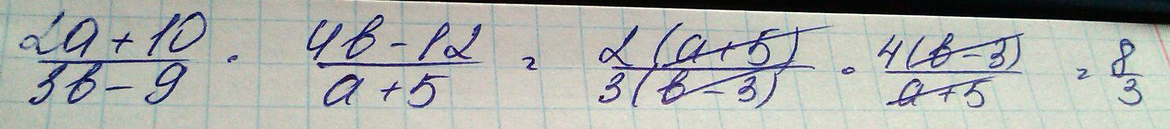
Выполните действия:
а) m + 2n/(дробная черта) m-n Х(умножить) m² - n²/(дробная черта) 5m+10m
б) х² - 2х +1/ х² - 25 : х-1/х² + 5х
Решение: $$ \frac{m+2n}{m-n}* \frac{m^{2}-n^2}{5m+10n}=\frac{m+2n}{m-n}* \frac{(m-n)(m+n)}{5(m+2n)}= \frac{m+n}{5} \\ \frac{x^2-2x+1}{x^2-25}: \frac{x-1}{x^2+5x}= \frac{(x-1)^2}{(x-5)(x+5)}: \frac{x-1}{x(x+5)}=\frac{(x-1)^2}{(x-5)(x+5)}* \frac{x(x+5)}{x-1}= \\ = \frac{(x-1)*x}{x-5} $$$$ 1) \frac{m+2n}{m-n} * \frac{ m^{2} - n^{2} }{5m+10n} = \frac{(m+2n)*(m-n)(m+n)}{(m-n)*5(m+2n)} = \frac{1*(m+n)}{5} = \frac{m+n}{5} \\ \frac{ x^{2} -2x+1}{ x^{2} -25} : \frac{x-1}{ x^{2} +5x} = \frac{ (x -1)^{2} }{ (x-5)(x+5)} : \frac{x-1}{ x(x+5)} =\frac{ (x -1)^{2} }{ (x-5)(x+5)}* \frac{x(x+5)}{x-1} = \\ =\frac{ (x -1)^{2} *x(x+5)}{ (x-5)(x+5)*(x-1)} = \frac{(x-1)*x*1}{x-5} = \frac{x(x-1)}{x-5} = \frac{ x^{2} -x}{x-5} $$
При умножении двух одинаковых десятичных дробей ученик получил в ответе число, оканчивающееся цифрой 7. Почему можно сказать, что он допустил ошибку?
Решение: При умножении одинаковых чисел получится ответ с четным числом на конце.
(Например 1,2*1,2=1,44)Десятичная дробь может оканчиваться цифрой: 1, 2, 3, 4, 5, 6, 7, 8, 9. Рассмотрим квадраты этих цифр: 1²=1; 2²=4, 3²=9, 4²=16, 5²=25, 6²=36, 7²=49, 8²=64, 9²=81. Как мы видим ни одно из них не оканчивается цифрой 7.

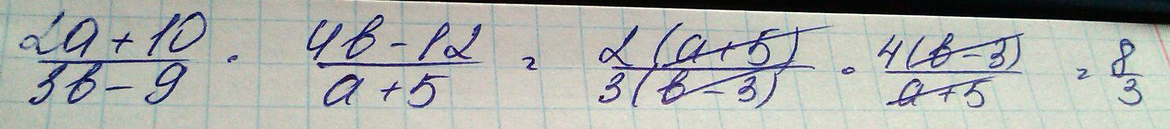
 Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...
Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...