дроби »
примеры с дробями - страница 11
Найдите значение а, при которым значение дроби равно нулю
α+4 5а-4 9-3а 7+3а
⁻⁻⁻⁻ ₋₋₋₋ -
а-4 А 9+ 3а 7-3а
Решение: Ответ: 9-3а.Дробь будет равна 0 если числитель дроби равен 0, знаменатель дроби не может равняться 0 так как на 0 делить нельзя. Поэтому в этих примерах необходимо числитель дроби приравнять к 0 и решить уравнение:
а+4=0 5а-4=0 9-3а=0 7+3а=0
а=-4 5а=4 -3а=-9 3а=-7
а=4/5 а=9/3=3 а=-7/3Найдите значение переменной при которых значение дроби равно нулю или докажите что таких значений нет
a)m-3/m
б)a/2a-5
в)a^2+1/a(a-1)
г)x(x-2)/x^2-3x+2
д)p(p+1)/p^2+7
Решение: А) чтобы дробь была равна нулю надо чтобы m-3 была равно нулю, приравниваем m-3=0; m=3 б) а=0 в) а^2+1 должна быть равно нулю поэтому приравниваем а^2+1=0 а^2 не = -1 => дробь не будет равна нулю г) х(х-2) должна быть равно нулю поэтому приравниваем х(х-2)=0 х=0 или х=2 д) р(р+1) должна быть равно нулю поэтому приравниваем р(р+1)=0 р=0 или р=-1Найдите значение х, при котором знаечение дроби х/3-х меньше значени двроби 6/х на 1
Решение: Ответ х =2$$ \frac{x}{3-x}+1= \frac{6}{x}|*x(3-x) = 0\\\\x^2+x(3-x)=6(3-x) |x = 0; x = 3\\\\x^2+3x-x^2=18-6x\\\\3x=18-6x\\\\3x+6x=18\\\\9x=18\\\\x=18:9\\\\x=2 $$
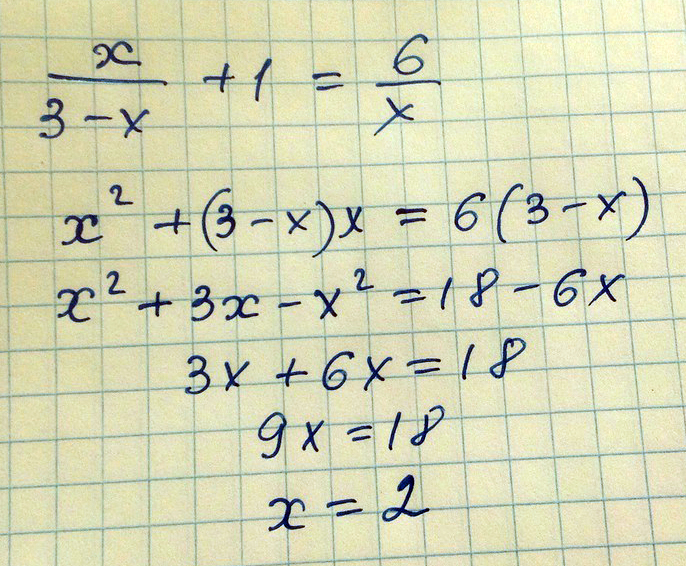
Найдите значение х при котором значение дроби х дробь 3-х меньше значения дроби 6хна 1
Решение: 6/х - х/(х-3) = 1, общий знаменатель х(3-х)18-6х-х2=3х-х2
9х=18
х=2
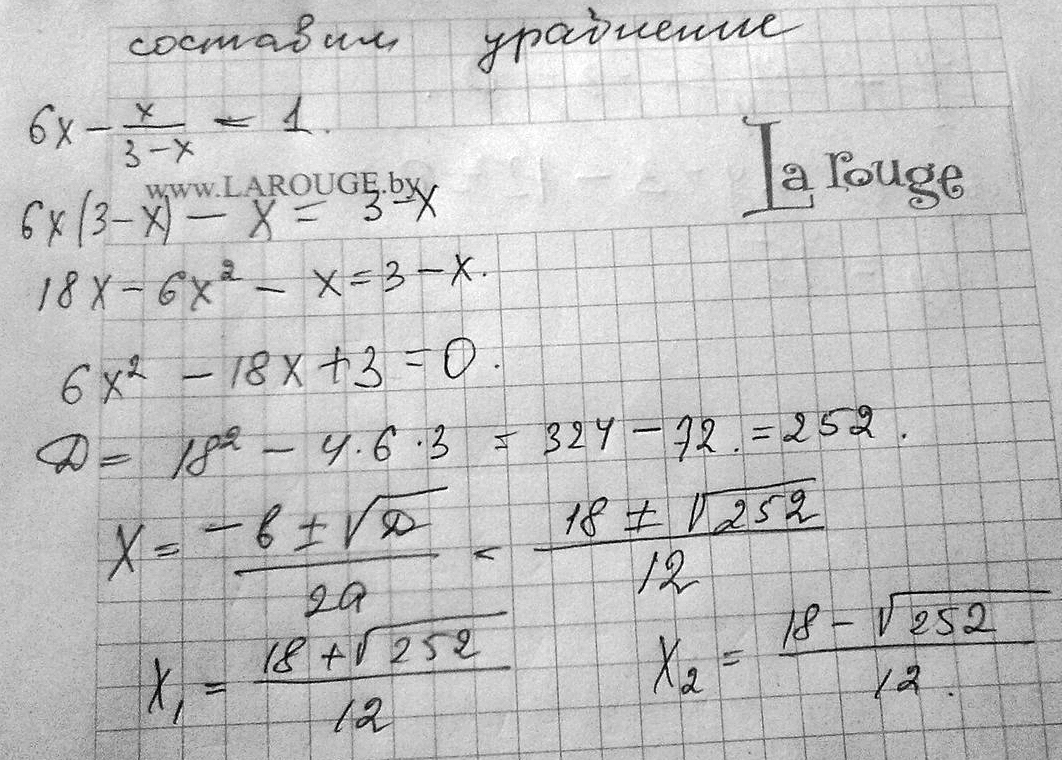
Найдите сумму всех значений х, при которых значение дроби 2х2+7х-4/х2+6х-2 равно 1
Решение: Домножим обе части на знаменатель( помня, что он не должен быть равен 0).
2х2+7х-4=х2+6х-2
х2+х-2=0
Можно решить уравнение, а можно воспользоваться теоремой Виета : сумма корней равна -1.
Все ж решим.
х2+х+0,25=2,25
(х+0,5)*(х+0,5)=1,5*1,5
решения
1 и -2. Сумма равна -1. ( проверим, что при обоих корнях знаменатель не 0!)

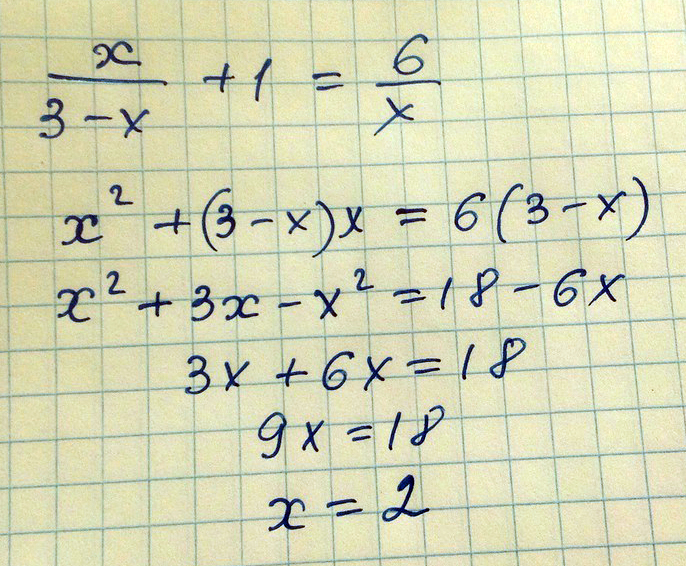
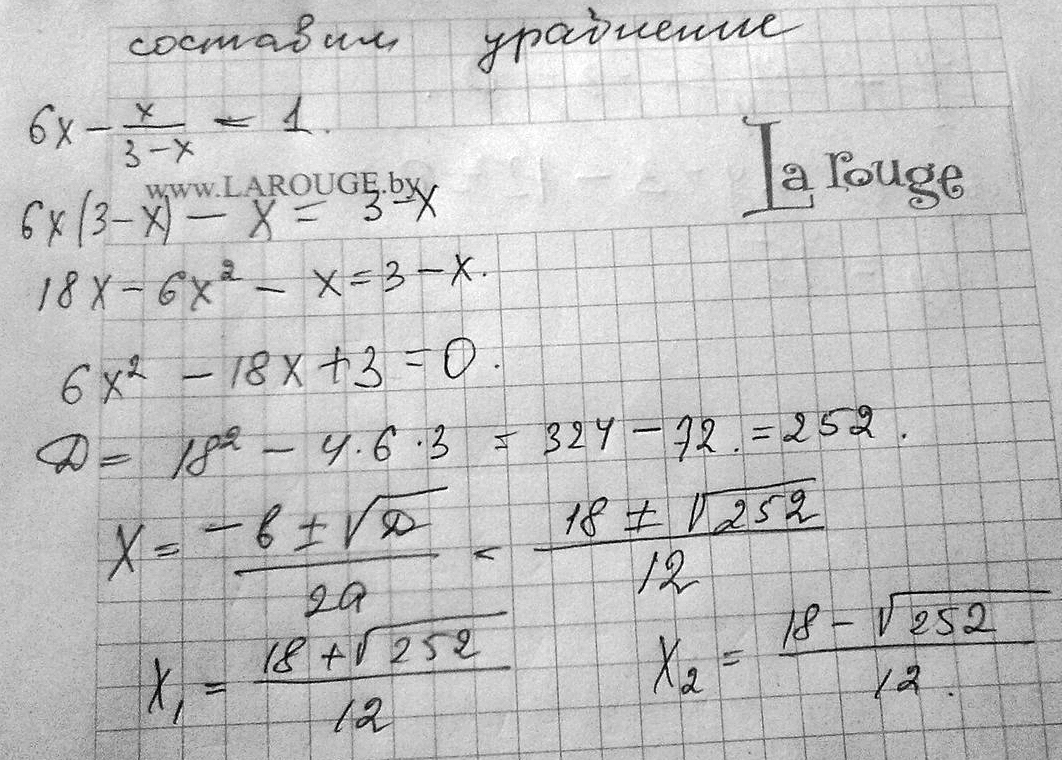
 Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...
Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...