дроби »

примеры с дробями - страница 19

  • Докажите, что при любых значениях а и b значение дроби числитель-ab(a-b)(a+b)
    знаменатель- 6. Значение дроби является целым числом. Докажите


    Решение: $$ \frac{-ab(a-b)(a+b)}{-6} =\frac{ab(a-b)(a+b)}{6} $$
    нужно доказать что это выражение делится на 3
    пусть а=х b=y где x и y делятся на 3
    тогда ab(a-b)(a+b) делится на 6 
    пусть а=х b=y+1
    тогда ab делится на 6 и ab(a-b)(a+b) делится на 6
    пусть а=х b=y-1
    тогда ab(a-b) делится на 6 и ab(a-b)(a+b) делится на 6
    пусть а=х+1 b=y
    тогда ab(a+b) делится на 6 и ab(a-b)(a+b) делится на 6

  • Выберите верные утверждения
    1) Число 777777 делится на 11
    2) Если к числу, кратному пяти, дописать слева цифру 4, то полученное число не будет делиться на 5
    3) Дана дробь, числитель и знаменатель которой -натуральные числа. Если к знаменателю дроби добавить единицу, а числитель оставить прежним, то значение дроби уменьшится
    4) Если число делится на 10, то оно делится и на 20

    Оченьнадо


    Решение: 1. верно, так как 7 чётное кол - во. 
    2. не верно, так как остаток будет 4. 
    3. верно, так как знаменатель увеличится.
    4. верно.
    Значит верные утверждения под номерами 1,3.4. 

    Верные ответы: 1;3; 4
    Неверные: 2, т. к. во втором, мы дописываем 4 в начало, то есть в конце число 5, при всех способах число делится на 5!

  • Выберите верные утверждения.
    1) Число 939 393 делится на 31.
    2) Если к числу, кратному пяти, дописать справа цифру 4, то полученное число будет делиться на 5.
    3) Дана дробь, числитель и знаменатель которой – натуральные числа. Если к числителю дроби слева дописать единицу, а знаменатель оставить прежним, то значение дроби увеличится.
    4) Если число делится на 5, то оно делится и на 10.


    Решение: 1) 939393/31=30303 верно
    2) любое число можно разделить на 5, но число с цифрой 4 справа на 5 без остатка не поделится. не верно
    3) возьмем например 25/100, если слева добавим 1 то получим 125/100, значение увеличилось. верно
    4) например числа 50 и 25 можно разделить на 5, но 25 на 10 без остатка не поделится. не верно

  • Прочитайте дроби 1/6 4/6 1/15 8/45 1/31 15/31 1/52 45/52 2/3 5/3 назовите числитель и знаменатель делимое и делитель


    Решение: одна (числитель, делимое) шестая
    четыре (числитель, делимое) шестых
    одна  (числитель, делимое)пятнадцатая
    восемь(числитель, делимое)  сорок пятых
    одна (числитель, делимое)  тридцать первых
    пятнадцать (числитель, делимое) тридцать первых
    одна (числитель, делимое) петдясят вторых
    сорок пять  (числитель, делимое) петдясят вторых
    две (числитель, делимое) третьи
    пять (числитель, делимое) третьих

  • нужно записать на математическом языке:
    1) величина дроби не изменится, если ее числитель и знаменатель умножить на одно и тоже число, не равное нулю.
    2) величина дроби не изменится, если ее числитель и знаменатель разделить на одно и тоже число, не равное нулю.
    3) чтобы найти число b, состовляющее p% от числа a, надо умножить число a на p и разделить полученное произведение на 100;
    4) чтобы найти число а, зная, что p% от него равны числу b, надо число b умножить на 100 и полученное произведение разделить на p;
    5) в верной пропорции произведение крайних членов равно произведению средних;
    6) если в верной пропорции поменять местами средние члены и крайние, то полученные пропорции также верны.


    Решение: $$ \frac{a}{b}=\frac{a*k}{b*k};keq0 \\ \frac{a}{b}=\frac{a/k}{b/k};keq0 \\ b=\frac{a*p}{100} \\ a=\frac{b*100}{p} \\ a:b=c:d;a*d=b*c \\ a:b=c:d;d:c=b:a $$

    решение смотри :

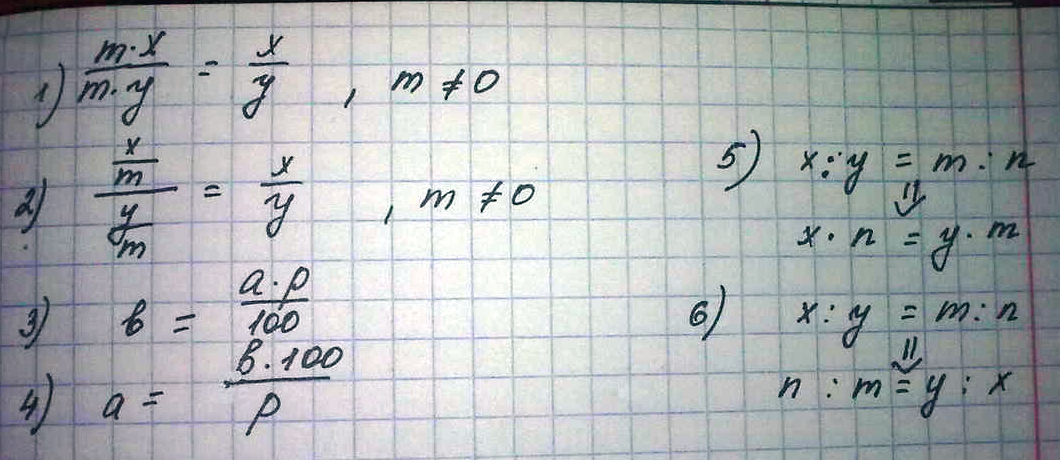
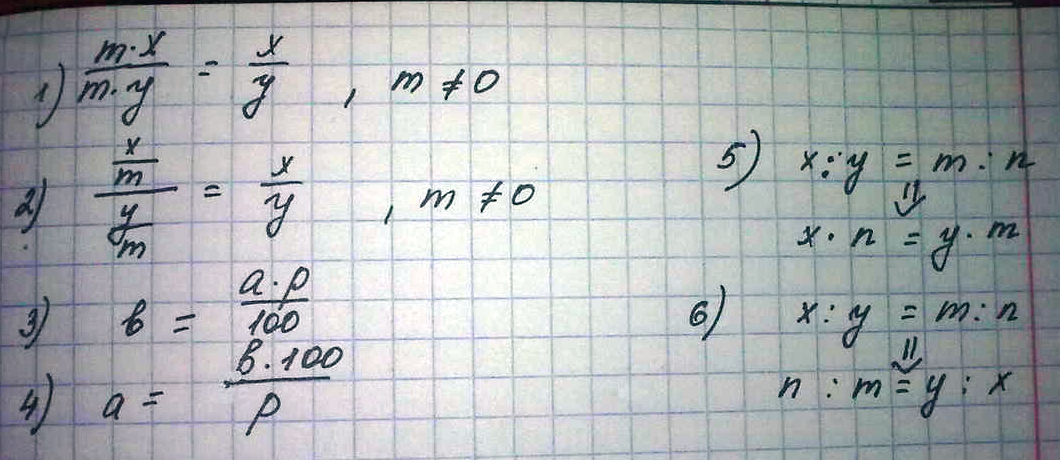
    frac a b frac a k b k keq frac a b frac a k b k keq b frac a p a frac b p a b c d a d b c a b c d d c b a решение смотри...
<< < 171819 20 21 > >>