примеры с дробями - страница 4
№865 Запишите числа: а) 1 000 000, 100 000, 10 000, 1000, 100, 10, 1, 1/100, 1/1000, 1/10 000, 1/100 000, 1/1 000 000 степенью с основанием 10 ; г) здесь тоже дроби со знаком / 1/625, 1/125, 1/25, 1/5, 1, 5, 25, 125, 625 степенью с основанием 5 3125=5^5 (рисунок№1)
Решение: а)1 000 000=10⁶100 000=10⁵
10 000=10⁴
1000=10³
100=10²
10=10¹
1=10⁰
1/100=10⁻²
1/1000 =10⁻³
1/10 000=10⁻⁴
1/100 000=10⁻⁵
1/1 000 000=10⁻⁶
г)
$$ \frac{1}{625}=\frac{1}{5^{4}}=5^{-4} $$
$$ \frac{1}{125}=\frac{1}{5^{3}}=5^{-3} $$
$$ \frac{1}{25}=\frac{1}{5^{2}}=5^{-2} $$
$$ \frac{1}{5}=\frac{1}{5^{1}}=5^{-1} $$
1=5⁰
5=5¹
25=5²
125=5³
625=5⁴
..............................
а) 10^6; 10^5; 10^4; 10^3; 10^2; 10^1; 10^0; 10^-2; 10^-3; 10^-4; 10^-5; 10^-6.
б) 5^-4; 5^-3; 5^-2; 5^-1; 5^0; 5^1; 5^2; 5^3;5^4.
Сравните по величене. Просто поставте знак. ( < ) (>) (=)
1) 65% и (дробь) три пятых
2) Дробь Две-целых, пять седьмых и 2, 73
3) дробь ( три четвёртых ) и одиннадцать пятнадцатых
4) модуль -3 и 2
5) -0,85 и -0,805
6) 0,05 мин и 5 с
Решение: 1) 65% > (дробь) три пятых2) Дробь Две-целых, пять седьмых < 2, 73
3) дробь ( три четвёртых ) > одиннадцать пятнадцатых
4) модуль -3 > 2
5) -0,85 < -0,805
6) 0,05 мин < 5 с
1) 65% > 3/5
3/5=0,6
65%=0.652) 2 5/7 < 2,73
2 5/7=2.714285714285713) 3/4 > 11/15
3/4=0.75
11/15=0.7334) |-3| > 2
5) -0,85 < -0,805
6) 0,05 мин < 5 с
\( \frac{2x+1}{x-3} \geq 1 \)
Решить, ))
(дробь в скобках модуля))
Решение: (2x+1)/(x-3) -1≥0
(2x+1-x+3)/(x-3)≥0
(x+4)/(x-3)≥0
x=-4 U x=3
+ _ +
-
-4 3
x∈(-∞;-4] U (3;∞)$$ \frac{2x+1}{x-3} \geq 1 \\ x-3 eq 0 \iff x eq 3 \\ \frac{2x+1}{x-3}-1 \geq 0 \iff \frac{2x+1-x+3}{x-3} \geq 0 \iff \frac{x+4}{x-3} \geq 0 \\ 1) x-3\ > \ 0 \iff x\ > \ 3 \\ x+4 \geq 0 \iff x \geq -4 \\ x \ > \ 3 \\ 2) x-3\ < \ 0 \iff x\ < \ 3 \\ x+4 \leq 0 \iff x \leq -4 \\ x \leq -4 \\ x \in (-\infty;-4];x \in (3;+\infty) $$
Преобразуйте в дробь выражение \(ab^{-3}-ba^{-3}; \\ a^2b+b^{-2}a;\)
Решение: $$ ab^{-3}-ba^{-3}= \frac{a}{b^3} - \frac{b}{a^3} = \frac{a^4-b^4}{a^3b^3} \\ a^2b+b^{-2}a=a^2b+ \frac{a}{b^2} = \frac{a^2b^3+a}{b^2} $$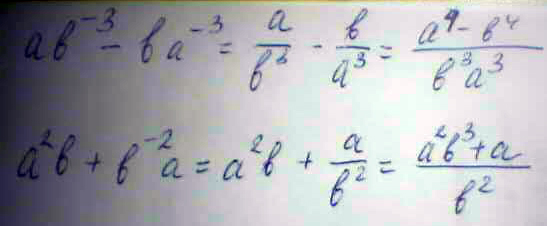
Преобразуйте в дробь выражение: \((3а^2*b^3)^{-1}*9^2*b\\a*b-b*a^{-1}\)
Решение: 1) (3а^2*b^3)^(-1)*9^2*b=(9a^2*b)/(3a^2*b^3)=сокращаем=3/(b^2)2)a*b-b*a^(-1)=ab-b/a=приводим к общему знаменателю=(a^2*b-b)/a=(b*(a^2-b))/a
1) (3а^2*b^3)^(-1)*9^2*b=(9a^2*b)/(3a^2*b^3)=3/(b^2)
2)a*b-b*a^(-1)=ab-b/a=(a^2*b-b)/a=(b*(a^2-b))/a
Ответы:(b*(a^2-b))/a 3/(b^2)

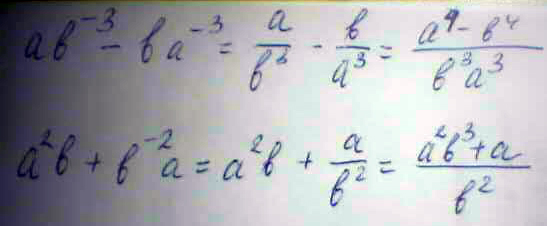
 Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...
Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...