график функции »
график линейной функции - страница 4
Постройте график линейной функции у=2х
Решение: Подставляете х и решаете
х=1 у=2
х=2 у=4
соеденяете точки, и график готов!Функция линейная
графиком функции являеиься прямая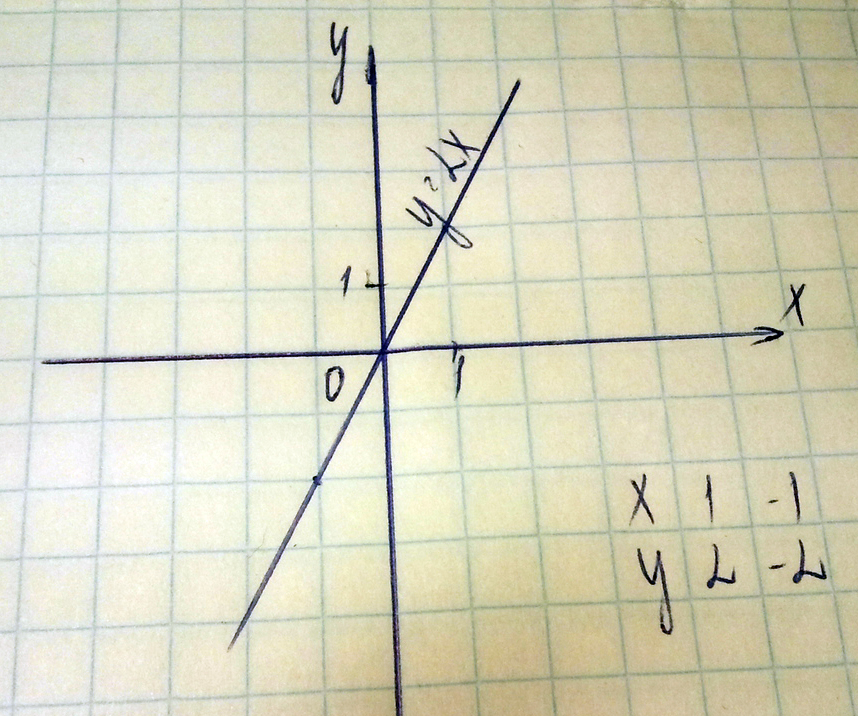
Составить график линейной функции у=3х-3
найти ось OX и OY
определить какие точки пренадлежат графику функции А(0,0) В(-4,10) С(5,12) D(1,0)
Решение: Найдем 2 точки, чтобы начертить график прямой у=3х-3 х=0 у=3*0-3=-3 1(0,3) y=0 0=3x-3 3x=3 x=1 2(1, 0)
чертите систему координат ОХ ОУ 2) находите точки (0 -3) и (1,0) через эти точки проводите прямую
2) A(0.0) 0=3*0-3=-3 НЕТ 0не равен -3
B(-4.10) 10=3*(-4)-3 10НЕ =-15 нет
С(5.12) 12=3*5-3=12 ДА
D(1.0) 0=3*1-3=0 ДАПостройте график линейной функции y=2x-3
Решение: Если Х = 0, то Y = -2 * 0 + 3 = 3.Если Y = 0, то -2 * Х + 3 = 0, откуда Х = 3/2 = 1,5.
Нанеси на координатную плоскость точки А (0; 3) и В (1,5 ; 0) и соедини их прямой. и запиши точки пересечения
y=2x-3
x 1 2 3 4
y -1 1 3 5
___________________
постройте график линейной функции Y=KX, если известно, что ему принадлежит точка: M(12; 48)
Решение: Подставим координаты токи в уравнение функции:y = kx
48 = k * 12
k = 4.
Итак, уравнение функции: y = 4x. График функции приложен.
Постройте график линейной функции y= -4x + 8. Найдите
Решение: у=-4х+8уравнение прямой, значит нужно две точки, чтобы её построить.
Берем х=0, у=8, то есть точка (0;8)
х=2, у=0, т. е. (2;0)
Чертим две прямые под углом 90 градусов.
отмечаем начало координат, единичный отрезок по каждой оси.
показываем положительное направление стрелками и отмечаем найденные точки.
проводим через них прямую линию, подписываем график.
Если нужно далее работаем с графиком.

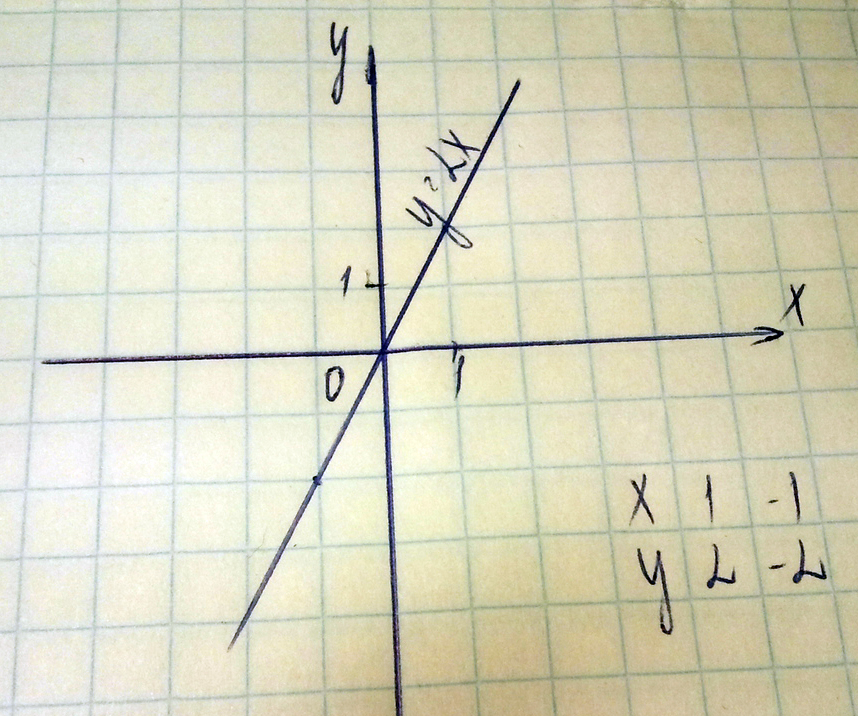
 Уравнение вида mx = n, к которому сводится любое линейное уравнение, может быть легко решено графически. На одном и том же рисунке построим графики двух функций: у = mx и у = n. Если эти графики пересекутся, то абсцисса точки пересечения и даст нам корень уравнения mx = n.
Если же эти графики не пересекутся, то это будет означать, что уравнение...
Уравнение вида mx = n, к которому сводится любое линейное уравнение, может быть легко решено графически. На одном и том же рисунке построим графики двух функций: у = mx и у = n. Если эти графики пересекутся, то абсцисса точки пересечения и даст нам корень уравнения mx = n.
Если же эти графики не пересекутся, то это будет означать, что уравнение... Рассмотрим некоторые вопросы поведения функций вида
$$ y=\frac{ax+b}{cx+d} \;\;\;(1) $$
где а, b, с и d - заданные числа, причем с отлично от нуля. Такие функции называются дробно-линейными (обычно, говоря о функциях вида (1), предполагают, что ad - bc \(\neq\) 0. Это условие мы заменяем здесь более простым условием с \(\neq\) 0.).
Прежде всего отметим, что дробно-линейная функция (1) определена при всех...
Рассмотрим некоторые вопросы поведения функций вида
$$ y=\frac{ax+b}{cx+d} \;\;\;(1) $$
где а, b, с и d - заданные числа, причем с отлично от нуля. Такие функции называются дробно-линейными (обычно, говоря о функциях вида (1), предполагают, что ad - bc \(\neq\) 0. Это условие мы заменяем здесь более простым условием с \(\neq\) 0.).
Прежде всего отметим, что дробно-линейная функция (1) определена при всех...