график функции »
график линейной функции - страница 9
Постройте график линейной функции у=0,2 х если х принадлежит [-5;3)
Решение: График будет принимать следующий вид. Только начинаться он будет на оси х от -5, а не от бесконечности, как показано на скрине. А на месте тройки на оси х нужно поставить незакрашенный кружочек, т. к. скобка круглая, и продолжаться он уже будет бесконечно в правую сторону.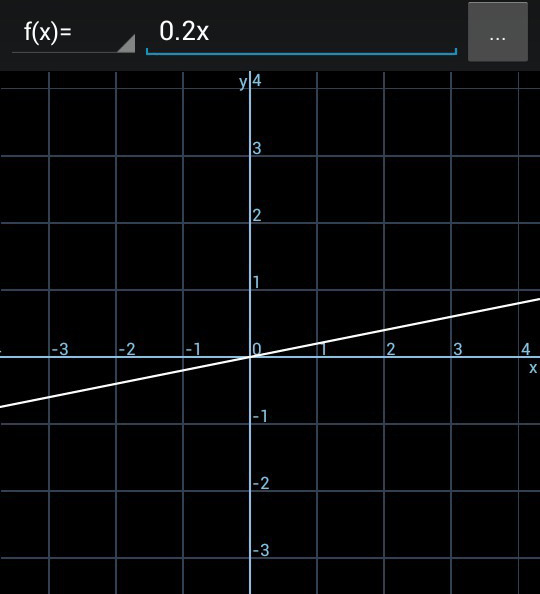
Постройте график линейной функции: а)y=2x; б)y=-3x; в)y=-6x; г)y=x
Решение: А) у= 2 х - это линейная функция, графиком является прямая, для построения достаточно 2- х точек 1) х = 0, у= 0.2) х= 1. у = 2
б) у=-3х - это линейная функция, графиком является прямая, для построения достаточно 2- х точек 1) х=0, у=0.2) х = 1, у = -3
в) у = -6х - это линейная функция, графиком является прямая, для построения достаточно 2- х точек 1) х = 0, у= 0.2) х= 1/2, у= -3
г) у=х - это линейная функция, графиком является прямая, для построения достаточно 2- х точек 1) х = 0, у= 0.2) х= 1, у= 1Построить график линейной функции 1)y=2х+5 2)-3х+5y=20
Решение: У=2х+5
х -2 -1 0 1 2
у 1 3 5 6 9
у=2*(-2)+5=1
у=2*(-1)=3
у=2*0=5 и т. д.
по этим координатам строим график
-3х+5у=20
у=20+3х \ 5
х -2 -1 0 1
у 14 17 20 23
строй по этим координатам график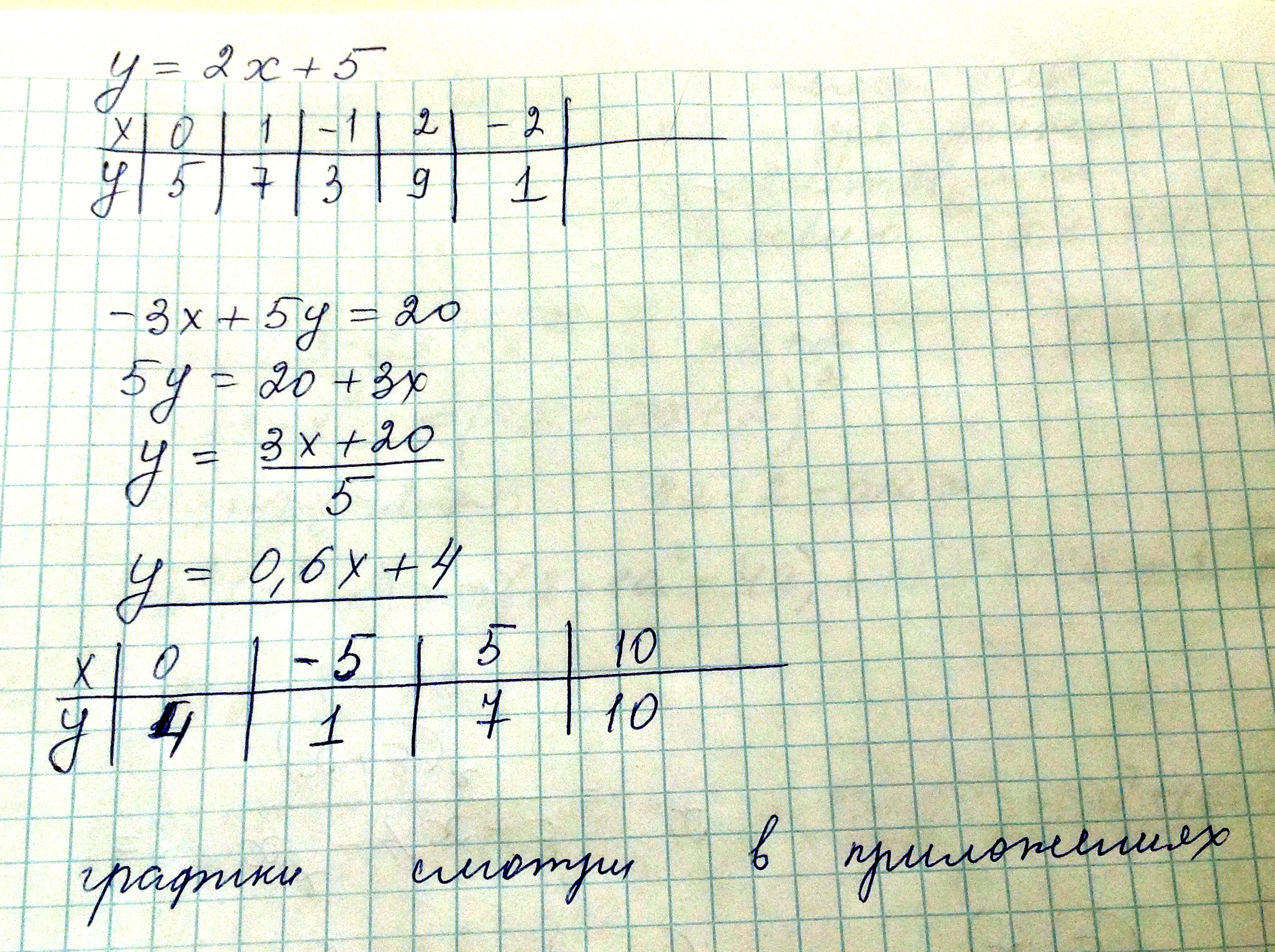
Постройте график линейной функции у=-2х+3 и с его помощью решите неравенство -2х+3 ≥ 1
Решение: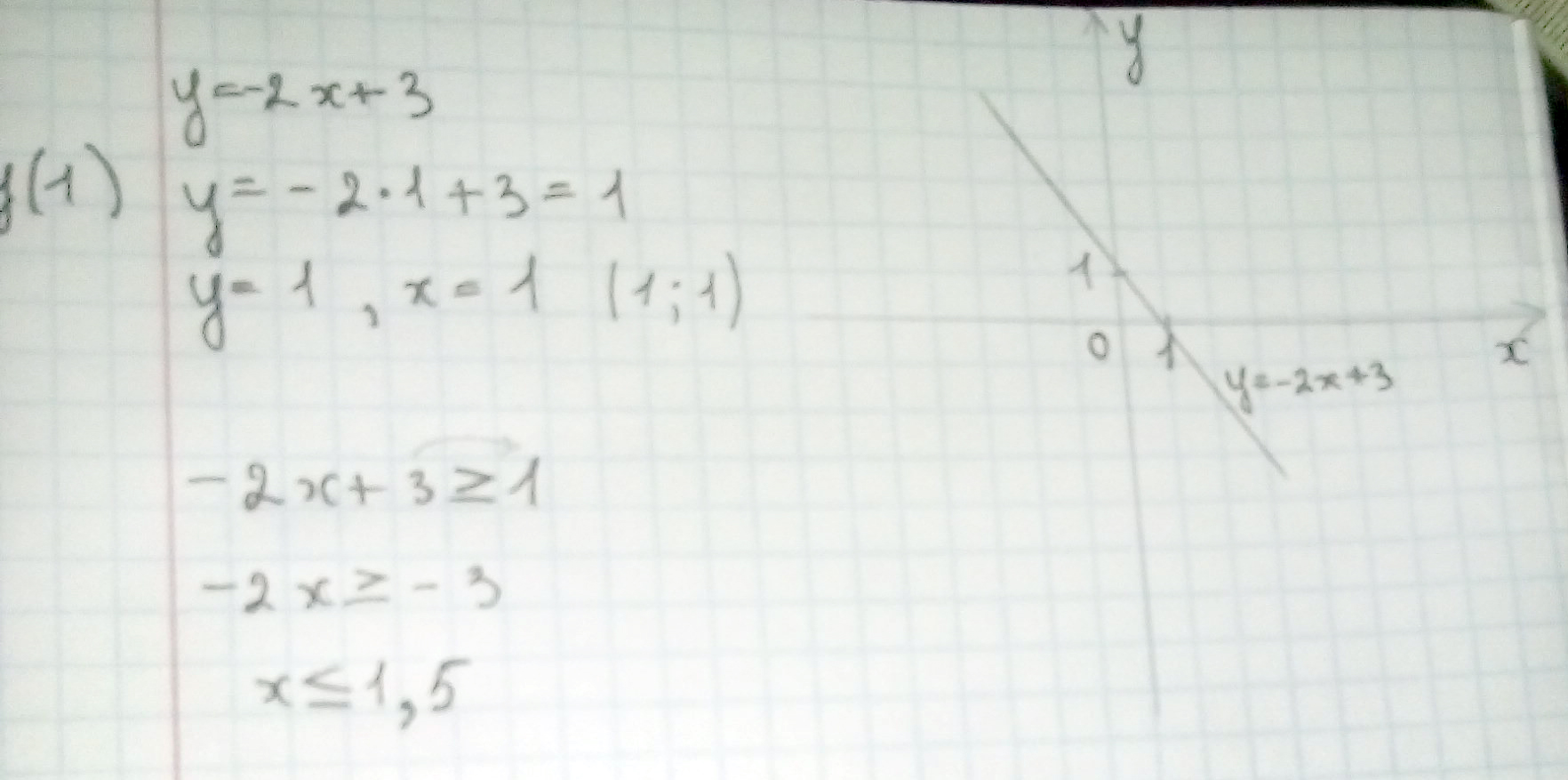
Постройте график линейной функции y= -4x+8 найдите а) значение y, соответствует значению x, равному 0, 1, 2, 3
Решение: Если х=0, то у=8; х=1, у=4; х=2, у=0; х=3, у=-4Если х=0, то у=-4*0+8=0+8=8;
если х=1, то у=-4*1+8=-4+8=4;
если х=2, то у=-4*2+8=-8+8=0;
если х=3, то у=-4*3+8=-12+8=-4;
чтобы построить график на оси х откладываете значения х, а на оси у откладываете соответствующие им значения у: (0;8); (1;4); (2;0); (3;-4) и соединяете эти точки линией, т. к. функция линейная.


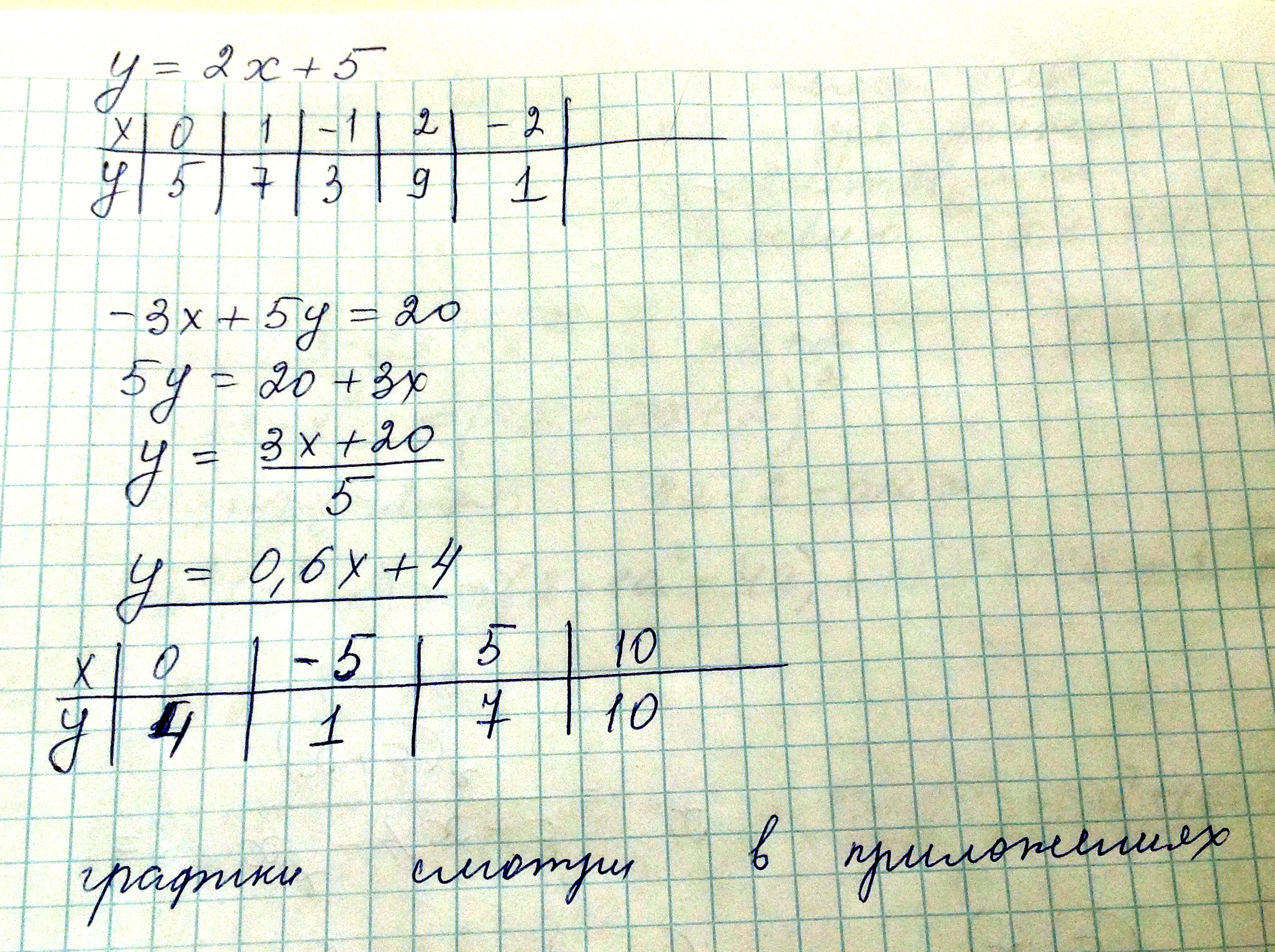
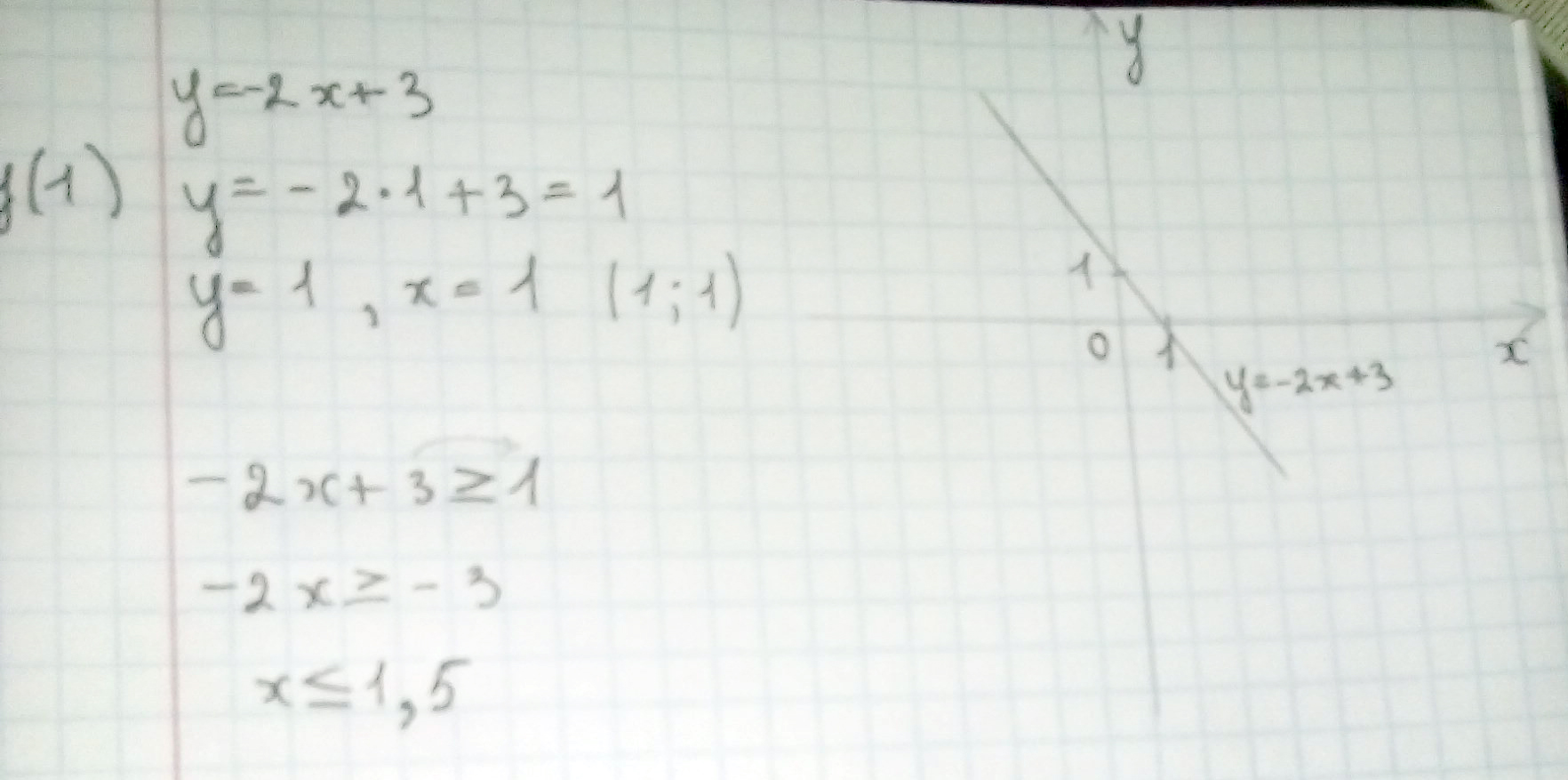
 Уравнение вида mx = n, к которому сводится любое линейное уравнение, может быть легко решено графически. На одном и том же рисунке построим графики двух функций: у = mx и у = n. Если эти графики пересекутся, то абсцисса точки пересечения и даст нам корень уравнения mx = n.
Если же эти графики не пересекутся, то это будет означать, что уравнение...
Уравнение вида mx = n, к которому сводится любое линейное уравнение, может быть легко решено графически. На одном и том же рисунке построим графики двух функций: у = mx и у = n. Если эти графики пересекутся, то абсцисса точки пересечения и даст нам корень уравнения mx = n.
Если же эти графики не пересекутся, то это будет означать, что уравнение... Рассмотрим некоторые вопросы поведения функций вида
$$ y=\frac{ax+b}{cx+d} \;\;\;(1) $$
где а, b, с и d - заданные числа, причем с отлично от нуля. Такие функции называются дробно-линейными (обычно, говоря о функциях вида (1), предполагают, что ad - bc \(\neq\) 0. Это условие мы заменяем здесь более простым условием с \(\neq\) 0.).
Прежде всего отметим, что дробно-линейная функция (1) определена при всех...
Рассмотрим некоторые вопросы поведения функций вида
$$ y=\frac{ax+b}{cx+d} \;\;\;(1) $$
где а, b, с и d - заданные числа, причем с отлично от нуля. Такие функции называются дробно-линейными (обычно, говоря о функциях вида (1), предполагают, что ad - bc \(\neq\) 0. Это условие мы заменяем здесь более простым условием с \(\neq\) 0.).
Прежде всего отметим, что дробно-линейная функция (1) определена при всех...