график функции »

найдите координату точек пересечения графика функции - страница 16

  • Найдите координаты точек пересечения с осями Ох и Оу графика функции, заданной формулой:
    1) у=-4х-16
    2) x^2-5х-6
    3) х^3 -8
    4) у=√х+1 -√4-х


    Решение: 1) y=4x-16 - прямая
      при y =0:
      4x-6 =0 -> x=1,5
      (1,5; 0) - пересечение с осью Х
      при х=0: у=-16
      (0; -16) - пересечение с осью Y
    2) y=x²-5x-6 - парабола
      при х=0: у=-6
      пересечение с осью y : (0; -6)
      при y =0:
    x²-5x-6=0
    x1=-1 x2=6
    y=0 y=0
      пересечение с осью х: (-1; 0) и (6;0)
    3) y=x³-8
     при у=0: х³=8 х=2 ; пересечение с осью х: (2;0)
     при х=0: у=-8; пересечение с осью у:  (0;-8)

    4) у=√(х+1) -√(4-х)
      при х=0: у=√1-√4=1-2=-1 пересечение с осью y: (0;-1)
      при у=0: 
    √(x+1) -√(4-x) =0
    √(x+1)=√(4-x)
    x+1=4-x
    2x=3
    x=1,5
    gпересечение с осью х: (1,5; 0)
      

  • Постройте график функции. Найдите координаты точек пересечения графика с осями координат.
    1)y=-x-2
    2)y=0,5x-3
    3)y=-1,5x+3
    4)y=1/3x+2
    5)y=-1/5x-1
    6)y=1/4x+1


    Решение: Для того, чтобы построить графики функций, нужно в каждом случае задать значения x, получим значения y. По найденным точкам строим графики. Точками пересечения графика с осями координат являются точки, где x= 0, это точка пересечения с осью y, и, наоборот, где y=0, это точка пересечения с осью x.
    1)y = -x - 2 x=0 y=-2 (пересечение с осью y)
      x=1 y=-3
      x=2 y=-4
      x=-2 y=0 (пересечение с осью x). И так далее.
    2) y=0,5-3 x=0 y=-3
      x=2 y=-2
      x=4 y=-1
      x=6 y=0
    3) y=-1,5+3 x=0 y=3
      x=2 y=0
    4)y=x/3+2 x=0 y=2
      x=3 y=3
      x=-6 y=0
    5)y=-x/5-1 x=0 y=-1
      x=5 y=-2
      x=-5 y=0
    6)y=x/4+1 x=0 y=1
      x=4 y=2
      x=-4 y=0

  • постройте график функции найдите координаты точек пересечения графика с осями координат у=-х-2


    Решение: При пересечении с осью ОХ y =0,
    тогда 0 = - x -2 ; x = -2
    координата (-2; 0)
    при пересечении с осью ОY x =0,
    тогда y = - 0 -2 ; y = -2
    координата (0; -2)
    строим график
    функция у = -х-2  - прямая линия
    для прямой линии достаточно двух точек - любых
    беру x = 5 ; y = -5-2 = -7
    беру x = - 5 ; y = 5-2 = 3
    отмечаю точки на координатной плоскости
    соединяю по линейке
    определяю точки пересечения и их координаты
    (-2; 0) (0; -2)
    график прилагается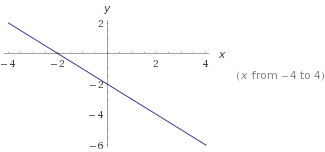

    При пересечении с осью ОХ y тогда   - x - x - координата - при пересечении с осью ОY x тогда y  - - y - координата - строим графикфункция у   -х-   - прямая линиядля прямой л...

  • Без построений найдите координаты точек R и S пересичения с осями абсцисс и ординат соответственно графика функции а) y=4x-8


    Решение: это линейная функция

    надо найти координаты двух точек и провести прямую. это и будет гпафик линейной функции

     а по вашему вопросу. всегда сначала принимают  Х за 0, тогда У = - 8

    это одна точка и её координаты  Х=0, У=-8

    а потом У принимают за 0, тогда Х = 2

    и это координаты второй точки Х=2,  У=0

  • Постройте график функции. Найдите координаты точек пересечения графика с осями координат:
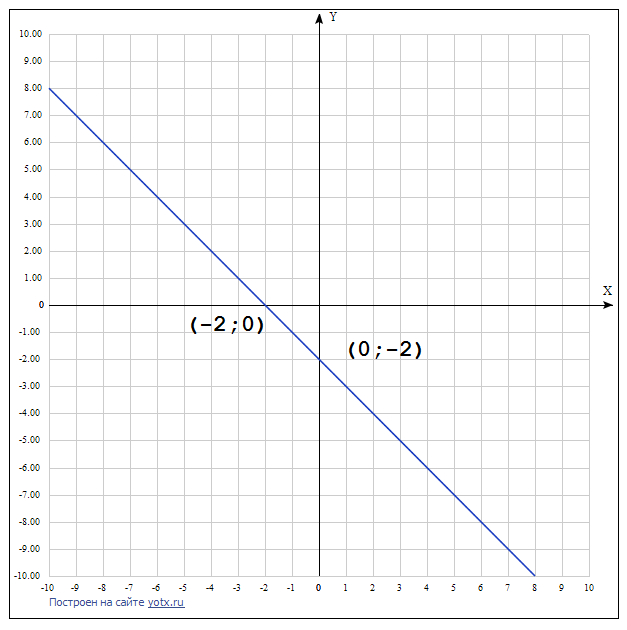
    1) у=-х-2
    2) у=1\3х +2
    3) у=0,2х+1


    Решение: $$ 1) y=-x-2 \\ \begin{array}{c|cc}x&-2&0\\y&0&-2\\\end{array} \\ 2) y=\frac{1}{3}x +2 \\ \begin{array}{c|cc}x&-6&0\\y&0&2\\\end{array} \\ 3) y=0,2x+1 \\ \begin{array}{c|cc}x&-5&0\\y&0&1\\\end{array} $$

    y -x- begin array c cc x amp - amp y amp amp - end array y frac x begin array c cc x amp - amp y amp amp end array y x begin array c cc x amp - amp y amp amp end array...
<< < 141516 17 18 > >>