график функции »

область определения функции - страница 6

  • 1. Решите уравнение корень 5 степени из (2x-7) +2=02.Найдите область определения функции f(x)=1/корень 4 степени из (5x-8)
    3.найдите все значения t,при которых равны значения выражений t+5 и корень из 2t^2 +19t+43
    4.упростите выражение (1/(2x^0.5+3^0.5) - 1/(2x^0.5 - 3y^0.5)) умножить на (2x-9y/2)


    Решение: Корень пятой степени равен -2 возведем обе части в степень 5.
    2x-7=(-2)^5=-32 2x=-32+7=-25 x=12.5

    выражение в знаменателе ≠0 5х-8≠0 х≠8/5
    5х-8>0← под корнем число большее 0 →x>8/5

    t+5=√(2t²+19t+43)
    t+5≥0 → t≥-5
    возводим обе части в квадрат → t²+10t+25=2t²+19t+43→
    t²+9t+18=0 корни по виетту t1=-3 t2=-6 этот корень меньше -5 и не годится.
    ответ -3

    разность дробей в примере 4 находим используя формулу разности квадратов.
    (2х^0.5-3y^0.5-2x^0.5-3y^0.5)/(4x^1-9y^1)=-6y^0.5/(4x-3y)
    умножим -6y^0.5*(2x-9y/2)/(4x-9y)=-6y^0.5(4x-9y)/2(4x-9y)=-3y^0.5=
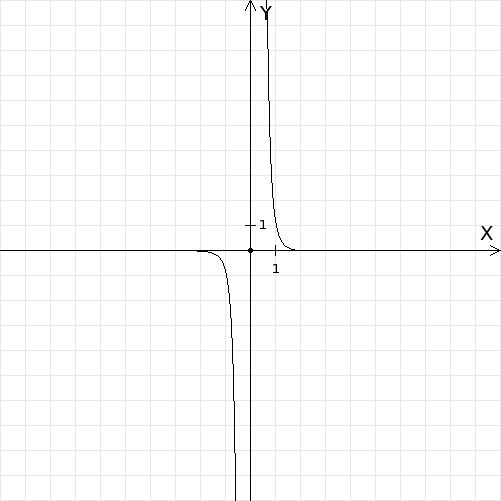
    =-3√y


  • Изобразить схематически график функции y=x в степени -5 и указать ее область определения и множество значений.


    Решение: $$ y=x^{-5}\\ y=\frac{1}{x^5}\\ xeq0\ $$

    D(y)=(-∞; 0) U (0; +∞)

    E(y)=(-∞; 0) U (0; +∞)

    На рисунку график ф-ции не должен касаться оси х, он близко к ней, но не пересекает.

    y x - y frac x xeq D y - U E y - U На рисунку график ф-ции не должен касаться оси х он близко к ней но не пересекает....

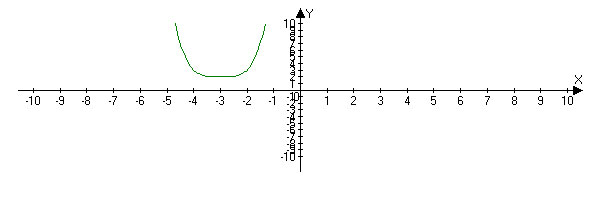
  • Построить график функции y=(x+3)в 4 степени+2. Указать область определения


    Решение: Строим обычную параболу y=x^4, потом сдвигаем ее вверх по оси Оу  на 4 единицы вверх, а потом сдвигаем слево по оси оХ на три единицы.
    координаты вершины (-3;2)
    Область определения: х - любое число

    Строим обычную параболу y x потом сдвигаем ее вверх по оси Оу  на единицы вверх а потом сдвигаем слево по оси оХ на три единицы.координаты вершины - Область определения х - лю...

  • Найти область определения функции 1) y(x)=корень из х - корень из 2-х 2) y=1/2х*корень из 1-х 3) y=1/х*корень из 1-2х 4) y=3 в степени 1/x 5) y= 1/5 встепени корень из х 6) y= 2 в степени корень из х-1 7) y= 0,2 в степени 1/x в квадрате


    Решение: 1) y(x)=корень из х - корень из 2-х ищем пересечение x,больше или равно0 и х меньше или равно 2 получаем от 0 до 2 обе скобки квадратные

    2) 2) y=1/2х*корень из 1-х х меньше 1 xe от - бесконечности до 1, обе скобка круглые (вопрос корень в числителе или в знаменателе, если в числителе то правая скобка квадратная)

    3) y=1/х*корень из 1-2х x меньше 1/2 от - бесконечности до 1/2 обе скобка круглые (вопрос корень в числителе или в знаменателе, если в числителе то правая скобка квадратная)

    4) y=3 в степени 1/x x не равно 0, от - беск до о в объединении от 0 до + беск

    все скобки круглые

     5) y= 1/5 в степени корень из х х больше или равно 0 от 0 до + бесконечн, первая скобка квадратная, вторая круглая

    6)  y= 2 в степени корень из х-1 x больше или равно 1 от 1 до + беск

    первая скобка квадратная, вторая круглая

  • Найдите область определения функцииy=log0,2(x в кубе - х в 4 степени)


    Решение:

    Логарифмическая функция определена на множестве положительных чисел, поэтому выражение стоящее под знаком логарифма должно быть положительным. Составляем неравенство:
    х³-х⁴>0
    Решаем методом интервалов:
    х³(1-х)>0
    Находим нули функции
    х³(1-х)=0
    х³=0  или  1-х=0
    х=0  х=1
    Точки х=0 и х=1 (отмечаем их пустым кружком, мы круглыми скобками) разбивают числовую прямую на три промежутка:
    _______(0)___________(1)________
    Находим знак на (1;+∞)
    10∈(1;+∞)
    10³(1-10)<0, значит на (1;+∞) ставим знак минус.
     И далее знаки чередуем.
    ____-___(0)_____+______(1)____-____

    О т в е т. D(y)=(0;1).

<< < 456 7 8 > >>